【JavaScript链表全攻略】：揭秘从基础到高级的链表秘密与性能优化

# 1. 链表的基础知识与概念解析

## 简介
链表是一种基本的数据结构，它由一系列节点组成，每个节点包含数据和指向下一个节点的引用。与数组不同，链表的元素不需存储在连续的内存空间，这使得链表在插入和删除操作上具有天然的优势。

## 基本概念
链表中的节点（Node）通常包含两部分：数据域和指向下一个节点的指针（或引用）。根据指针方向的不同，链表可以分为单向链表、双向链表和循环链表。单向链表的节点只能指向下一个节点，双向链表的节点除了指向前一个节点外，还能指向后一个节点，循环链表则形成一个闭环，最后一个节点指向头节点。

## 链表的使用场景
链表常用于实现栈、队列和哈希表等抽象数据类型。在需要频繁插入和删除操作的场景中，链表相比数组更高效，因为它不需要像数组那样移动大量元素。在算法和软件工程中，理解链表及其操作是基本功，它也是学习更复杂数据结构和算法的基石。

# 2. 链表的数据结构原理与实现

## 2.1 链表的内部结构解析
### 2.1.1 节点（Node）的定义与属性
在链表这一数据结构中，节点是构成链表的基本单元。每个节点包含了两个主要部分：一个是存储数据的变量，另一个是指向下一个节点的引用（在双向链表中还包括指向前一个节点的引用）。通常，节点在编程语言中以类或结构体的形式表示。

class Node {
    constructor(data) {
        this.data = data; // 节点存储的数据
        this.next = null; // 指向下一个节点的引用
    }
}

在上述JavaScript代码中，我们定义了一个名为`Node`的类，用于创建链表节点。`data`属性用于存储节点信息，`next`属性用于存储指向下一个节点的引用。在双向链表中，会增加一个`prev`属性来指向前一个节点。

### 2.1.2 链表的类型：单向链表、双向链表和循环链表
链表根据节点间链接的方式不同，可以分为单向链表、双向链表和循环链表。单向链表中，每个节点仅包含一个指向下一个节点的引用。双向链表中每个节点含有两个链接，分别指向前一个和下一个节点。而循环链表则与单向链表类似，不同之处在于最后一个节点指向第一个节点，形成一个循环。

理解不同链表的结构特点对于后续分析其操作复杂度和应用场景具有重要意义。单向链表结构简单，易于实现，但在寻找某个节点的前驱节点时效率低下。双向链表则允许双向遍历，可以快速访问前驱节点，但内存开销更大。循环链表适合解决一些需要遍历所有节点的问题，如解决多路归并问题。

## 2.2 链表的创建与基本操作
### 2.2.1 链表的初始化和节点的添加
链表的初始化是指创建一个空的链表，即头节点为空。随后，我们可以进行节点添加操作。添加节点时，主要分为头部添加和尾部添加两种情况。

class LinkedList {
    constructor() {
        this.head = null; // 初始化头节点为空
    }

    append(data) {
        let newNode = new Node(data);
        if(this.head === null) {
            this.head = newNode;
        } else {
            let current = this.head;
            while(current.next !== null) {
                current = current.next;
            }
            current.next = newNode;
        }
    }
}

以上代码片段展示了如何实现链表的初始化和尾部添加节点的逻辑。`append`方法首先创建一个新节点，然后检查链表是否为空。如果为空，则将新节点设置为头节点；如果不为空，则遍历至链表尾部，将新节点添加至尾部。

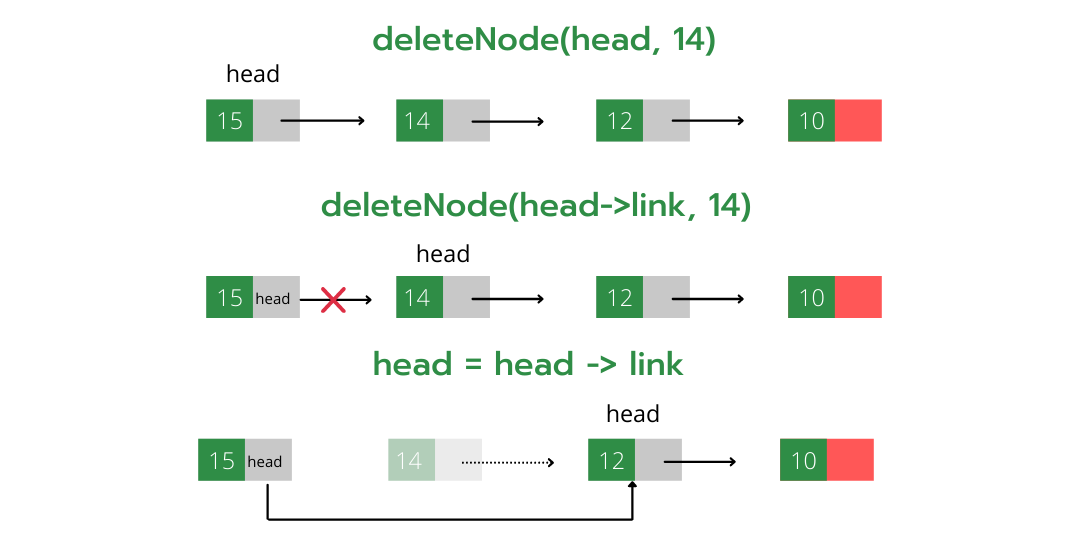
### 2.2.2 链表节点的查找、删除和修改
链表的查找、删除和修改操作都需要先遍历链表找到指定位置的节点。查找操作简单直接，只需根据索引或特定值遍历链表即可。删除和修改操作则需要在找到相应节点后，调整其前后节点的链接。

class LinkedList {
    // ... 其他方法

    find(data) {
        let current = this.head;
        while(current !== null) {
            if(current.data === data) {
                return current;
            }
            current = current.next;
        }
        return null; // 未找到
    }

    delete(data) {
        if(this.head === null) return null;
        if(this.head.data === data) {
            this.head = this.head.next;
            return;
        }
        let current = this.head;
        while(current.next !== null) {
            if(current.next.data === data) {
                current.next = current.next.next;
                return;
            }
            current = current.next;
        }
    }

    update(data, newData) {
        let node = this.find(data);
        if(node !== null) {
            node.data = newData;
        }
    }
}

这些方法演示了如何在链表中查找、删除和修改节点。`find`方法通过遍历链表查找含有特定数据的节点。`delete`方法在删除节点时考虑了删除的是头节点和非头节点两种情况。`update`方法则是查找节点并更新其数据。这些操作的时间复杂度通常为O(n)，因为最坏情况下需要遍历整个链表。

## 2.3 链表的时间复杂度分析
### 2.3.1 常见链表操作的时间复杂度
链表的操作复杂度主要与其节点的遍历相关。头节点操作（如头部添加节点）的时间复杂度为O(1)，因为它不依赖链表长度。而查找、删除和修改操作通常为O(n)，因为最坏情况下需要遍历整个链表。

### 2.3.2 与数组操作的时间复杂度对比
相比于数组，链表在添加和删除操作上表现更佳，尤其是在不需要随机访问元素的情况下。数组在添加或删除操作时，若不是在尾部，通常需要移动元素，时间复杂度为O(n)。而链表无需移动，因此时间复杂度为O(1)。但在查找元素时，链表需要O(n)的时间复杂度，因为需要从头节点开始遍历，而数组可以利用索引直接访问，时间复杂度为O(1)。

通过上述对链表基本操作的时间复杂度分析，我们可以看出链表在某些特定场景下具有更好的性能。而下一章节将探讨链表的高级操作与算法应用，进一步加深对链表性能和实际应用的理解。

# 3. 链表的高级操作与算法应用

## 3.1 链表的排序算法

### 3.1.1 插入排序和归并排序在链表中的实现

在处理链表这种非连续存储的数据结构时，排序算法的选择和实现与数组有所不同。由于链表的节点通过指针相互链接，不支持直接的随机访问，因此某些排序算法在链表上运行起来比在数组上更高效。

#### 插入排序的链表实现

插入排序是一种简单直观的排序算法，它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。在链表中实现插入排序时，由于链表的移动元素的成本较低，只需要改变节点之间的链接即可，相比数组这种数据结构有其独特的优势。

class ListNode {
  constructor(val) {
    this.val = val;
    this.next = null;
  }
}

function insertionSortList(head) {
  if (!head || !head.next) return head;

  let sorted = new ListNode(0); // 创建一个哨兵节点，方便插入操作
  let current = head;
  while (current) {
    let prev = sorted; // 寻找插入位置
    let next = current.next; // 保存当前节点的下一个节点
    // 寻找插入位置
    while (prev.next && prev.next.val < current.val) {
      prev = prev.next;
    }
    current.next = prev.next; // 插入节点
    prev.next = current;
    current = next; // 移动到下一个节点
  }
  return sorted.next;
}

在上述代码中，首先创建了一个哨兵节点（`sorted`），然后通过遍历链表中的每个节点，在已排序部分寻找合适的插入点，实现插入操作。这种方法的时间复杂度为O(n^2)，但是因为链表节点的移动只是改变链接，所以其性能表现通常优于数组的插入排序实现。

#### 归并排序的链表实现

归并排序是一种分治算法，其思想是将原始链表分成较小的链表，直到每个小链表只有一个元素，然后将小链表归并成较大的链表，直到最后只有一个排序完成的链表。

function mergeTwoLists(l1, l2) {
  let dummy = new ListNode(0);
  let current = dummy;

  while (l1 && l2) {
    if (l1.val < l2.val) {
      current.next = l1;
      l1 = l1.next;
    } else {
      current.next = l2;
      l2 = l2.next;
    }
    current = current.next;
  }

  current.next = l1 || l2;
  return dummy.next;
}

function sortList(head) {
  if (!head || !head.next) return head;

  // 快慢指针找到中间节点
  let prev = null, slow = head, fast = head;
  while (fast && fast.next) {
    prev = slow;
    slow = slow.next;
    fast = fast.next.next;
  }

  prev.next = null;

  let l1 = sortList(head);
  let l2 = sortList(slow);

  return mergeTwoLists(l1, l2);
}

上述代码中，`sortList` 函数首先找到链表的中间节点，将链表分成两半，然后分别对两半进行归并排序，最后通过`mergeTwoLists`函数将两个已排序链表合并。归并排序的时间复杂度为O(nlogn)，但是需要额外的空间，这在数组中可能是一个问题，但在链表中就不那么显著了。

### 3.1.2 快速排序、堆排序等复杂排序算法的应用

快速排序和堆排序等复杂排序算法在链表上的实现不太常见，因为它们需要随机访问的能力，或者要维护一个额外的数据结构来确保性能。因此，这些排序算法通常在数组上使用，而不是链表。

然而，快速排序的链表版本依然存在，它通常通过记录链表的长度来改进分区操作，但整体性能不如数组版本。在链表上实现复杂排序算法并不经济，所以一般较少采用。对于链表数据结构，通常会优先考虑适合其特性的排序算法，比如之前提到的插入排序和归并排序。

在实践应用中，对链表进行排序应当考虑到数据结构的特性、排序算法的特性以及它们之间的性能权衡。

## 3.2 链表的遍历技巧

### 3.2.1 迭代遍历和递归遍历的区别与选择

链表的遍历是数据处理中的基础操作，分为迭代遍历和递归遍历两种主要方法。它们在概念上有着明显的区别，具体选用哪一种方法取决于数据处理的场景以及对于性能和内存使用的考虑。

#### 迭代遍历

迭代遍历使用循环结构来遍历链表，通常使用一个外部的循环控制变量，如一个指针，从头节点开始逐个访问链表中的节点，直到访问到链表的末尾。迭代遍历的方式易于理解和实现，且在大多数情况下，它的性能更优，因为它不需要额外的内存来存储递归调用的栈信息。

function iterateLinkedList(head) {
  let current = head;
  while (current) {
    // 处理当前节点
    console.log(current.val);
    current = current.next;
  }
}

在上述代码示例中，通过一个while循环遍历链表，直到`current`节点为`null`。这种方式简单直接，也适用于大多数遍历需求。

#### 递归遍历

递归遍历是通过将问题分解为更小的子问题来解决，即对当前节点的操作完成后，通过递归调用自身来处理链表中的下一个节点。递归遍历的实现通常更为简洁，代码更加直观，但其缺点在于它需要额外的空间来存储函数调用栈。

function recursiveLinkedList(head) {
  if (!head) return;

  // 处理当前节点
  console.log(head.val);

  // 递归调用处理下一个节点
  recursiveLinkedList(head.next);
}

递归方式的代码通常更为简洁，但需要注意的是，在链表很长的情况下，可能会由于栈溢出而导致程序崩溃。

在实际应用中，选择迭代还是递归取决于问题的大小和特定需求。迭代遍历通常更高效，特别是在处理大型链表时，而递归遍历则在代码简洁性和可读性方面更胜一筹。

### 3.2.2 深度优先搜索（DFS）和广度优先搜索（BFS）在链表中的应用

链表由于其结构的特殊性，通常不作为实现图算法的首选数据结构。然而，在某些特定的场景下，深度优先搜索（DFS）和广度优先搜索（BFS）这两种图的遍历算法也可以在链表上实现。

#### 深度优先搜索（DFS）

深度优先搜索通常用递归来实现，它尽可能深地搜索每个分支，直到分支的末端再回溯。在链表中，由于节点之间没有直接的“相邻”节点关系，因此实现DFS较为复杂，且并不常用。

如果链表被用来表示图的边，则可以使用DFS来遍历节点。但在纯粹的链表结构中，DFS的实现会失去其在图结构中的特殊意义。

#### 广度优先搜索（BFS）

广度优先搜索使用队列来实现，逐层访问图的节点。在链表中实现BFS可能意味着将节点存入队列，并按顺序访问它们。然而，由于链表没有随机访问的特性，BFS的实现效率不如数组等其他数据结构。

function bfsLinkedList(head) {
  let queue = [];
  let current = head;
  while (current) {
    console.log(current.val);
    if (current.next) {
      queue.push(current.next);
    }
    current = queue.shift();
  }
}

此代码片段演示了如何在链表上实现广度优先搜索，将链表节点存入队列，并依次从队列中取出以访问。

在实践中，广度优先搜索和深度优先搜索主要用于图的遍历，并且它们在数组或邻接表这样的数据结构上实现起来更为合适和高效。然而，在了解和学习这些算法时，尝试在不同的数据结构上实现它们，可以加深对算法思想的理解。

## 3.3 链表与其他数据结构的结合

### 3.3.1 链表与栈和队列的结合应用

链表与其他数据结构结合使用时，可以创建出更强大且高效的复合数据结构。例如，链表可以与栈和队列这两种常见的数据结构结合，利用各自的优势来优化特定操作的性能。

#### 链表与栈的结合

栈是一种后进先出（LIFO）的数据结构，而链表可以提供高效的动态数组功能。结合它们，可以实现一个既能快速增删末尾元素又能保持元素顺序的数据结构。

例如，可以使用链表来实现一个栈，其中`push`和`pop`操作对应于在链表末尾添加或删除节点。这种方式的优点是操作的时间复杂度为O(1)，但在实际应用中，会比使用数组实现的栈消耗更多的内存。

class Stack {
  constructor() {
    *** = null;
    this.size = 0;
  }
  push(val) {
    let newNode = new ListNode(val);
    if (this.size === 0) {
      *** = newNode;
    } else {
      newNode.next = ***;
      *** = newNode;
    }
    this.size++;
  }
  pop() {
    if (this.size === 0) return null;
    let poppedNode = ***;
    *** = ***.next;
    this.size--;
    return poppedNode.val;
  }
}

在这个简单的栈实现中，链表的头节点作为栈顶，这样可以保证`pop`和`push`操作的高效性。

#### 链表与队列的结合

队列是一种先进先出（FIFO）的数据结构。通过链表实现队列，可以使得`enqueue`（入队）和`dequeue`（出队）操作的时间复杂度均为O(1)。链表实现的队列可以通过一个头指针和尾指针来维护，其中头指针指向队列的前端，尾指针指向队列的后端。

class Queue {
  constructor() {
    this.front = null;
    this.rear = null;
    this.size = 0;
  }
  enqueue(val) {
    let newNode = new ListNode(val);
    if (this.size === 0) {
      this.front = this.rear = newNode;
    } else {
      this.rear.next = newNode;
      this.rear = newNode;
    }
    this.size++;
  }
  dequeue() {
    if (this.size === 0) return null;
    let removedNode = this.front;
    this.front = this.front.next;
    if (this.front === null) {
      this.rear = null;
    }
    this.size--;
    return removedNode.val;
  }
}

在这个队列实现中，`enqueue`操作增加新节点到链表尾部，而`dequeue`操作则从链表头部移除节点。

链表与栈和队列的结合使用，展示了如何通过不同数据结构的特性来优化特定的操作和算法实现，体现了数据结构组合的灵活性和实用性。

### 3.3.2 链表与树结构的结合：平衡树和B树

链表结构通常不用于直接表示树结构，因为链表缺乏足够的随机访问能力。然而，树结构中的节点通常会使用指针（在编程语言中表现为对象或结构体的引用）来相互连接，这与链表节点使用指针连接的原理是一致的。因此，链表可以作为树节点的一部分，以支持树的动态性质。

#### 链表与平衡树的结合

平衡树，如AVL树或红黑树，是二叉搜索树的扩展，它们通过旋转操作来保持树的平衡性。树节点通常包含数据以及指向其子节点（左子节点和右子节点）的指针，这些指针实际上就是链表节点中的“next”指针。

class TreeNode {
  constructor(value) {
    this.value = value;
    this.left = null;
    this.right = null;
  }
}

在上述代码中，每个`TreeNode`节点包含了两个链表节点，分别指向下个节点。这使得平衡树能够动态地在任意位置添加或删除节点，并保持树的平衡状态。

#### 链表与B树的结合

B树是一种自平衡的树数据结构，它维护了排序的数据，并允许搜索、顺序访问、插入和删除在对数时间内完成。B树的节点可能包含多个子节点，每个节点内部使用链表来维护子节点的顺序。

class BTreeNode {
  constructor(t) {
    this.keys = []; // 节点存储的键值
    this.children = []; // 子节点指针的链表
    this.leaf = true; // 是否为叶节点
    this.t = t; // B树的阶数
  }
}

在B树节点的实现中，`children`数组实际上可以看作是一种链表结构，其中每个节点通过数组索引连接。B树通过这种方式支持了较大的分支因子，并通过一系列的分裂和合并操作来保持树的平衡。

通过上述示例可以看出，链表的使用并不局限于其自身的结构，而是可以通过与其它数据结构的结合，丰富了其应用场景和功能。在实现复杂的数据结构时，理解各种数据结构的特性及其组合使用的方式对于设计出高效解决方案至关重要。

# 4. JavaScript中的链表实践

## 4.1 JavaScript中的链表实现
### 4.1.1 使用ES6类和原型链创建链表

在JavaScript中，链表可以通过类和原型链来实现。使用ES6的新特性，可以让我们更简单、直观地创建和操作链表。下面是一个简单的单向链表实现的例子：

class Node {
    constructor(data) {
        this.data = data;
        this.next = null;
    }
}

class LinkedList {
    constructor() {
        this.head = null;
    }

    append(data) {
        const newNode = new Node(data);

        if (!this.head) {
            this.head = newNode;
            return;
        }

        let current = this.head;
        while (current.next) {
            current = current.next;
        }
        current.next = newNode;
    }

    // 其他链表操作方法...
}

// 使用链表
const list = new LinkedList();
list.append(1);
list.append(2);
list.append(3);

#### 代码逻辑解读
1. `Node` 类用于创建链表节点，每个节点包含数据 `data` 和一个指向下一个节点的指针 `next`。
2. `LinkedList` 类用于创建链表，包含一个 `head` 属性指向链表的头节点。
3. `append` 方法用于在链表末尾添加新节点，通过循环找到链表的最后一个节点，并将其 `next` 指针指向新节点。

### 4.1.2 链表操作方法的封装和扩展

链表操作方法的封装和扩展是提高链表可用性的关键。我们需要实现如插入、删除、查找、反转等操作：

class LinkedList {
    // ...（Node类和LinkedList的构造函数）

    insert(position, data) {
        const newNode = new Node(data);
        if (position === 0) {
            newNode.next = this.head;
            this.head = newNode;
        } else {
            let current = this.head;
            let previous;
            let index = 0;

            while (current !== null && index < position) {
                previous = current;
                current = current.next;
                index++;
            }

            if (previous !== null) {
                previous.next = newNode;
                newNode.next = current;
            }
        }
    }

    // 其他链表操作方法...
}

// 使用链表
const list = new LinkedList();
list.insert(0, 'Head');
list.insert(1, 'Tail');

#### 代码逻辑解读
1. `insert` 方法允许我们在链表的指定位置插入一个新节点。它首先检查是否是在头节点插入，如果是，则直接修改 `head` 指针。
2. 如果不是在头节点插入，它会遍历链表找到正确的插入点，并更新前后节点的 `next` 指针，完成插入操作。

## 4.2 链表在现代Web应用中的作用

### 4.2.1 虚拟DOM和React中的链表应用

虚拟DOM是React的核心概念之一，它使用链表来管理DOM的更新。链表在其中的作用是高效地插入和删除节点，对应到DOM操作即为高效的DOM更新。

#### React中的链表使用示例

// 假设的React Fiber结构，使用链表管理任务
class FiberNode {
    constructor(tag, pendingWork) {
        this.tag = tag;
        this.pendingWork = pendingWork;
        this.child = null;
        this.sibling = null;
        this.return = null;
    }
}

// 创建链表结构来组织任务
const rootFiber = new FiberNode('Root', null);

// 这是链表的一部分，实际上React会有更复杂的结构来处理异步更新
rootFiber.child = new FiberNode('Child', 'ChildWork');
rootFiber.child.sibling = new FiberNode('Sibling', 'SiblingWork');

### 4.2.2 JavaScript链表在数据结构库中的应用案例

许多JavaScript库中都用到了链表，以实现特定的数据结构，例如栈、队列等。使用链表可以提供动态数据结构，避免了数组在动态扩容时的性能损耗。

#### 基于链表实现的栈示例

class Stack {
    constructor() {
        *** = null;
        this.size = 0;
    }

    push(data) {
        const newNode = new Node(data);
        newNode.next = ***;
        *** = newNode;
        this.size++;
    }

    pop() {
        if (!***) {
            throw new Error('Cannot pop from an empty stack');
        }
        const data = ***.data;
        *** = ***.next;
        this.size--;
        return data;
    }

    // 其他栈操作方法...
}

## 4.3 链表性能优化策略

### 4.3.1 内存管理和垃圾回收对链表的影响

在JavaScript中，内存管理是自动进行的，但是合理地使用链表可以减少内存泄漏的风险。链表的动态内存分配意味着只有实际使用的节点才会占用内存。

#### 内存管理分析
- 链表节点的创建和销毁是即时的，可以按需分配和释放内存，从而减少不必要的内存占用。
- 然而，如果链表使用不当，例如长期保存大量无用的节点引用，垃圾回收机制无法及时释放这些内存，会导致内存泄漏。

### 4.3.2 减少链表操作开销的技巧和最佳实践

链表操作的效率对性能有显著的影响。为了避免不必要的性能开销，我们应该遵循一些最佳实践：

#### 链表操作最佳实践
- 避免在遍历链表时修改链表结构，这可能会导致迭代器失效或其他问题。
- 使用哨兵节点（dummy node）来简化边界条件的处理，特别是在进行插入和删除操作时。
- 在频繁操作的场景下，考虑使用双向链表或循环链表来提高访问和操作的效率。

通过以上实践，我们可以更有效地利用链表，减少不必要的操作开销，并提升整体性能。在现代Web应用中，链表仍是一个非常重要的基础数据结构，它的高效和灵活性使其在数据操作中发挥着不可替代的作用。

# 5. 链表的未来趋势与研究方向

## 5.1 链表在新兴技术中的潜力探索

随着科技的快速发展，新兴技术领域对于数据结构的要求也越来越高。链表作为一种基础且灵活的数据结构，其在新兴技术中的潜力不容小觑。

### 5.1.1 链表在区块链技术中的应用前景

区块链技术的底层数据结构可以看作是一种特殊的链表——链式区块。每一个区块都包含了一定数量的交易记录，这些区块通过哈希值相互链接，形成一条链。

- **区块间的链式链接**：链表的特性使得区块链能够高效地追加新区块，因为只需改变最后一个区块的指针即可，无需移动其他区块。
- **去中心化的数据存储**：在区块链中，链表的节点可以分布在全球不同的服务器上，这种去中心化的存储方式使得数据更加安全和难以篡改。
- **智能合约与链表**：智能合约的执行依赖于状态转换，链表可以有效地管理这些状态的转换记录。

### 5.1.2 物联网（IoT）中链表数据同步的创新应用

物联网技术依赖于大量设备的数据采集和同步，链表在这一领域的应用同样值得关注。

- **数据收集与存储**：链表可以用来存储各个IoT设备的实时数据，其动态结构特别适合于频繁的插入和删除操作。
- **数据同步机制**：在IoT设备间同步数据时，链表可以作为临时存储结构，以实现设备间高效的数据共享和更新。

## 5.2 链表理论的深化与算法发展

链表作为数据结构中的经典代表，其理论研究也在不断深化，并与现代算法研究相结合，推动链表在实际应用中的优化和创新。

### 5.2.1 算法复杂度理论对链表研究的影响

算法复杂度理论对链表的研究有着深远的影响。算法的效率往往取决于数据结构的选择。

- **时间复杂度与空间复杂度**：链表的时间复杂度在查找操作上为O(n)，但在插入和删除操作上可以达到O(1)。这使得链表在某些特定算法设计中特别有优势。
- **算法优化**：针对链表的特性，研究者提出了许多优化算法复杂度的策略，比如缓存最近访问过的节点以加快查找速度等。

### 5.2.2 链表在并行计算和分布式系统中的优化方向

并行计算和分布式系统对数据结构提出了新的挑战，链表的优化方向也逐渐向这些新领域倾斜。

- **并发访问控制**：在多线程环境中，链表节点的并发访问控制变得尤为重要。研究者们在设计锁机制、原子操作等方面做出了大量工作。
- **分布式链表**：分布式链表将传统链表的概念扩展到多台机器上。节点不再局限于单一内存空间，而是分布在不同的物理机器上，这对链表的设计和实现提出了新的挑战。

总之，链表作为一种基础数据结构，其未来的研究和发展方向与多个前沿技术领域息息相关。通过对链表的不断研究和优化，我们可以期待它在新兴技术中发挥更大的作用。