【深度学习】：Z-Score方法，特征缩放的艺术

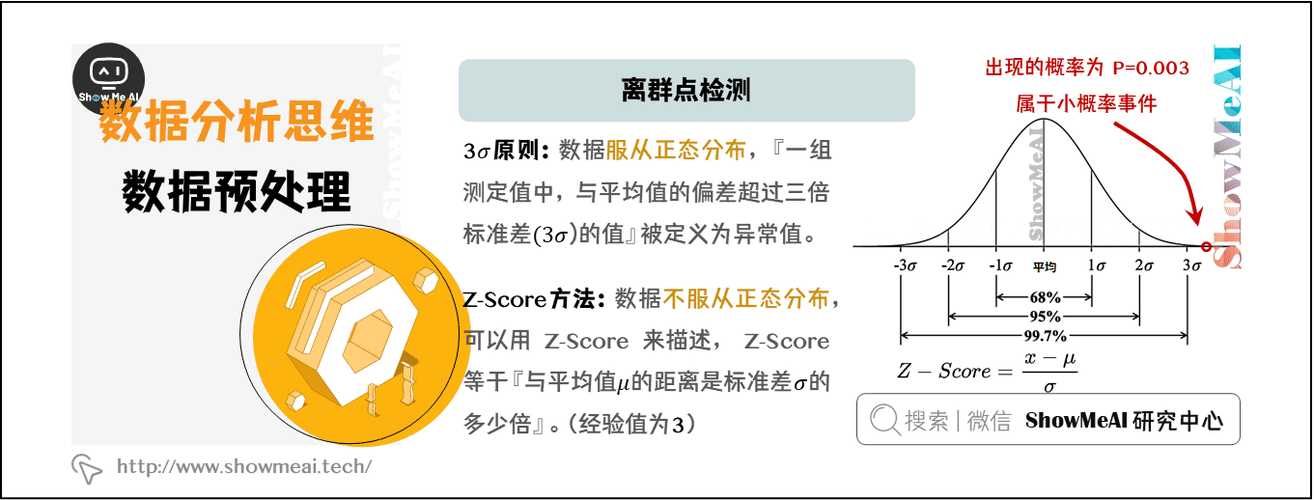
# 1. Z-Score方法基础与重要性

在数据科学领域，Z-Score方法是一种基本而强大的工具，用于标准化和异常值检测。该方法以数学形式定义了数据点与整体数据集平均值的相对距离，通常以标准差的单位来衡量。Z-Score的计算涉及三个关键要素：数据点值、数据集的平均值和标准差。

## 1.1 Z-Score的定义和公式

Z-Score公式为 `(X - μ) / σ`，其中 `X` 表示观测值，`μ` 是平均值，而 `σ` 是标准差。使用Z-Score可以将任何数据集中的数据转换为具有零均值和单位方差的形式。这样一来，数据点之间的比较变得公平，且与数据集的规模和分布无关。

## 1.2 Z-Score在数据分析中的作用

该方法不仅有助于理解和比较数据点，而且在异常值检测和数据预处理中尤为关键。异常值可以定义为与其它数据点显著不同的点，往往暗示错误或重要的统计信息。Z-Score提供了一种量化异常值的方法，并且因为其单位为标准差，所以可以根据经验法则较容易地判断异常值。

理解Z-Score对于任何分析数据的IT专业人士来说都是至关重要的，它不仅帮助更好地理解数据，还可以优化机器学习模型的性能。

# 2. Z-Score理论详解

### 2.1 标准化与Z-Score的数学原理

#### 2.1.1 数据分布的标准化概念

标准化是将数据转换成均值为0，标准差为1的分布形式。这一过程称为标准化处理或Z分数标准化，是统计学中用于数据标准化的一种方法。在机器学习中，标准化处理后的数据有助于消除不同特征量纲的影响，使得数据具有可比性，这在很多算法中是一个重要的预处理步骤。

标准化的数学公式如下：

\[ Z = \frac{(X - \mu)}{\sigma} \]

其中，\(X\) 是原始数据，\(\mu\) 是数据的平均值，\(\sigma\) 是标准差。标准化处理之后，数据集中的每个特征值\(Z\)，都表示原始数据与均值的偏差度量，以标准差为单位。

#### 2.1.2 Z-Score公式的推导

推导Z-Score的过程涉及到统计学中的标准化方法。假设我们有一组数据 \(X_1, X_2, ..., X_n\) ，首先计算均值 \(\mu\) 和标准差 \(\sigma\)：

\[ \mu = \frac{\sum_{i=1}^{n} X_i}{n} \]

\[ \sigma = \sqrt{\frac{\sum_{i=1}^{n} (X_i - \mu)^2}{n}} \]

接着，我们可以使用公式对每个数据点 \(X_i\) 计算其Z-Score：

\[ Z_i = \frac{X_i - \mu}{\sigma} \]

通过Z-Score处理后，我们得到一组新的数据 \(Z_i\)，这些数据的均值是0，标准差是1，从而达到数据标准化的目的。

### 2.2 Z-Score在特征缩放中的作用

#### 2.2.1 特征缩放的基本概念

特征缩放是数据预处理中的一个关键步骤，特别是在涉及到距离计算的算法中，如K-最近邻(KNN)和K均值(K-Means)聚类。特征缩放通过将数据缩放到一个标准范围内，确保所有特征都具有相同的影响度，从而避免某些特征由于数值范围大而占据主导地位。

#### 2.2.2 Z-Score与其他特征缩放方法的对比

Z-Score标准化只是众多特征缩放方法中的一种。与之相比较常用的有最小-最大缩放（Min-Max Scaling）方法，它将数据缩放到[0, 1]的范围内。使用Z-Score标准化的优势在于它不受异常值的强烈影响，而最小-最大缩放则对异常值非常敏感，可能会导致模型对异常值产生偏见。

对比两种方法，Z-Score更适合在数据集包含离群点的情况下使用，因为它的鲁棒性更强。然而，如果数据集中的所有数值数据都是正数，并且没有极端值，使用最小-最大缩放可能更为合适。

### 2.3 Z-Score方法的适用场景与局限性

#### 2.3.1 适用数据类型和场景分析

Z-Score标准化适用于连续数值型数据，并且最好是对称分布的数据。对于那些呈正态分布的数据，Z-Score标准化非常有效，因为它依赖于数据的均值和标准差，而这些参数在正态分布数据中是理想的统计度量。

在实际应用中，例如，在需要对数据进行可视化分析（如绘制散点图）或在进行统计推断（如假设检验）之前，Z-Score标准化非常有用。它也可以用在数据清洗阶段，帮助检测和处理异常值。

#### 2.3.2 Z-Score的局限性和注意事项

尽管Z-Score有许多优势，但它也有一些局限性。例如，当数据集中有离群值时，Z-Score可能会被这些离群值所影响，导致标准化的结果出现偏差。因此，在进行Z-Score标准化之前，通常需要进行离群值检测和处理。

此外，Z-Score标准化要求数据必须是近似正态分布的。如果数据偏离正态分布，Z-Score可能不会提供一个合理的标准化结果。在这些情况下，可能需要考虑使用其他非线性变换或者分位数标准化等替代方法。

为了弥补这些局限性，数据科学家们需要对数据进行彻底的探索性数据分析，以了解数据的分布情况，并据此决定是否适用Z-Score标准化。在实际操作中，数据预处理是一个需要不断迭代和优化的过程，Z-Score标准化只是这个过程中众多工具之一。

# 3. Z-Score方法实践应用

## 3.1 使用Python实现Z-Score标准化

### 3.1.1 Python代码基础及库的介绍

在Python中，实现Z-Score标准化可以使用多个库，其中最常用的是NumPy和SciPy。NumPy提供了强大的数组对象，以及各种数学运算；而SciPy提供了许多用于科学计算的高级函数，包括统计函数。

在开始编写代码之前，需要确保已经安装了这些库。可以使用pip命令来安装：

pip install numpy scipy

### 3.1.2 编写Z-Score标准化脚本的步骤

Z-Score标准化的步骤可以被分解为以下简单的几个步骤：

1. 计算数据集的平均值（mean）。
2. 计算数据集的标准偏差（standard deviation）。
3. 将每个数据点减去平均值，然后除以标准偏差。

以下是一个用Python实现Z-Score标准化的示例代码：

import numpy as np

def z_score_standardization(data):
    mean = np.mean(data)
    std_dev = np.std(data, ddof=1)  # 设置ddof=1是为了计算样本标准偏差
    return (data - mean) / std_dev

# 示例数据
data = np.array([50, 51, 52, 53, 54])
standardized_data = z_score_standardization(data)
print("原始数据:", data)
print("标准化后的数据:", standardized_data)

在上述代码中，我们首先导入了NumPy库，并定义了一个函数`z_score_standardization`来进行Z-Score标准化。我们使用了`np.mean`来计算平均值，`np.std`来计算标准偏差，并设置`ddof=1`以得到样本标准偏差而非总体标准偏差。之后，我们对一个示例数组`data`进行了标准化处理，并打印结果。

对于实际应用中的大规模数据集，可能需要对数据进行分割处理，然后分别进行Z-Score标准化，以避免内存溢出等问题。

## 3.2 Z-Score在机器学习中的应用实例

### 3.2.1 数据预处理的重要性

在机器学习中，数据预处理是关键的一步，它直接影响到模型的训练效果和预测准确性。数据预处理包括数据清洗、特征选择、特征转换等多个方面。其中，特征转换的核心目的是减少特征之间的相关性，使特征尺度统一化，提高模型的泛化能力。

Z-Score标准化就是特征转换的一个重要工具，通过将特征的值调整到具有0均值和1标准偏差的分布上，它帮助模型在学习过程中更快地收敛，并且可以避免因为特征尺度差异过大而导致的数值计算问题。

### 3.2.2 实例演示：使用Z-Score提升模型性能

假设我们正在处理一个回归问题，并且有一个数据集包含两个特征`feature1`和`feature2`。我们将演示如何使用Z-Score标准化来提升模型性能。

首先，我们创建一个数据集，并使用Z-Score标准化方法对特征进行预处理：

from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

# 生成模拟数据集
X, y = make_regression(n_samples=100, n_features=2, noise=10)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 将训练集和测试集的数据标准化
X_train_zscore = (X_train - np.mean(X_train, axis=0)) / np.std(X_train, axis=0)
X_test_zscore = (X_test - np.mean(X_test, axis=0)) / np.std(X_test, axis=0)

# 训练模型
model = LinearRegression()
model.fit(X_train_zscore, y_train)

# 使用标准化后的测试集进行预测
y_pred = model.predict(X_test_zscore)

# 计算模型的均方误差
mse = mean_squared_error(y_test, y_pred)
print("均方误差（MSE）:", mse)

通过上述代码，我们首先生成了一个模拟的回归数据集，并划分了训练集和测试集。然后，我们对训练集和测试集的特征使用Z-Score方法进行标准化，并训练了一个线性回归模型。最后，我们使用标准化后的测试集进行预测，并计算了模型的均方误差。

可以预期的是，使用Z-Score标准化的数据会比原始数据训练出来的模型有更小的均方误差，从而证明了Z-Score标准化在提升模型性能方面的作用。

## 3.3 Z-Score方法的故障排除与优化

### 3.3.1 实际应用中的常见问题

在实际应用中，Z-Score标准化可能会遇到几个常见问题：

- **数值稳定性问题**：当数据集中的某些特征值非常接近0时，标准偏差也会接近0，这会导致除数趋近于0，从而引起除法错误。这种情况下，可能需要对这些特征进行特殊处理或者使用其他类型的特征缩放技术。
- **异常值的影响**：Z-Score方法对异常值非常敏感。如果数据中包含异常值，它们会对均值和标准偏差造成很大影响，进而影响Z-Score的计算结果。

### 3.3.2 性能优化和调试技巧

针对数值稳定性问题，可以采取以下策略：

- **添加小的常数**：向数据中添加一个小的常数（例如1e-9），可以防止分母为零的情况发生。
- **使用更鲁棒的标准化技术**：例如使用中位数和四分位数进行标准化。

处理异常值的问题，可以考虑以下方法：

- **数据清洗**：在进行标准化之前先对数据进行清洗，去除或修正异常值。
- **异常值检测**：使用统计学方法，如IQR（四分位距）等来检测和处理异常值。
- **使用截断的Z-Score方法**：限制Z-Score的绝对值，比如只处理|Z| < 3的值，以避免极端值影响。

通过上述故障排除和优化方法，可以有效提高Z-Score方法在各种应用中的可靠性和准确性。

# 4. Z-Score方法的高级应用

在数据分析和机器学习领域，Z-Score方法不仅仅限于数据预处理，它在统计学、非参数方法以及大数据环境下的高级应用，都为其增添了新的维度。本章节将深入探讨Z-Score方法在这些高级场景下的应用，并分析其优化策略。

## 4.1 结合统计学深入理解Z-Score

### 4.1.1 统计学中的中心极限定理与Z-Score

中心极限定理是统计学中的一个基础定理，它说明在一定条件下，大量独立随机变量之和会趋向于正态分布，即使这些随机变量本身并不服从正态分布。Z-Score正是在中心极限定理的基础上，通过标准化的方法将样本数据转换为正态分布的Z分数。

在实践中，中心极限定理为Z-Score方法提供了理论支持。Z-Score利用样本的均值和标准差，将数据转换成标准正态分布，从而使得我们可以用统一的标准来比较不同样本或数据集中的数据点。

import numpy as np

# 假设有来自非正态分布的样本数据
data = np.random.exponential(size=1000)

# 计算均值和标准差
mean = np.mean(data)
std_dev = np.std(data)

# 计算Z-Score
z_scores = (data - mean) / std_dev

### 4.1.2 Z-Score在异常值检测中的应用

异常值检测是数据预处理中的一个重要环节。Z-Score方法在异常值检测中非常有用，因为偏离均值多个标准差的数据点很可能是异常值。例如，如果数据点的Z-Score绝对值大于3，那么这个数据点就很有可能是异常值。

# 定义异常值的阈值
threshold = 3

# 找出异常值
outliers = np.where(np.abs(z_scores) > threshold)

# 输出异常值
outlier_values = data[outliers]

## 4.2 非参数方法与Z-Score的结合

### 4.2.1 非参数统计方法简介

非参数统计方法是指在数据分析过程中不依赖于数据分布的特定参数（如正态分布的均值和标准差）的方法。非参数方法对数据的分布形态要求不严格，因此适用于各种分布类型的数据。

在与Z-Score结合时，非参数方法可以用于处理那些不满足正态分布假设的数据集。Z-Score方法通过非参数变换，可以减少对数据分布形态的依赖，从而拓宽其适用范围。

### 4.2.2 结合非参数方法的Z-Score应用

结合非参数方法的Z-Score应用通常用于处理偏态分布或包含异常值的数据集。一个典型的应用场景是，先使用非参数方法（如中位数和四分位数）去除异常值，然后对剩余的数据应用Z-Score标准化。

# 使用非参数方法预处理数据
Q1 = np.percentile(data, 25)
Q3 = np.percentile(data, 75)
IQR = Q3 - Q1

# 去除异常值
filtered_data = data[(data >= (Q1 - 1.5 * IQR)) & (data <= (Q3 + 1.5 * IQR))]

# 对预处理后的数据应用Z-Score标准化
filtered_data_mean = np.mean(filtered_data)
filtered_data_std_dev = np.std(filtered_data)
z_scores_filtered = (filtered_data - filtered_data_mean) / filtered_data_std_dev

## 4.3 大数据环境下的Z-Score优化策略

### 4.3.1 分布式计算对Z-Score方法的影响

在大数据环境下，数据量级往往达到TB甚至PB级别，单机处理能力已经无法满足需求，必须使用分布式计算框架。分布式环境下处理Z-Score时，数据可能分散在多个节点上，因此需要一种能够在分布式环境中有效计算均值和标准差的方法。

Apache Spark等大数据处理框架提供了分布式数据处理的能力，可以利用这些工具来高效地计算大规模数据集的Z-Score。

### 4.3.2 大数据框架下的Z-Score实践策略

在大数据框架如Apache Spark中，实现Z-Score通常需要执行以下步骤：

1. 使用框架提供的聚合函数计算整体数据集的均值和标准差。
2. 将这些全局统计数据广播到各个节点。
3. 在各个节点上使用全局统计数据对本地数据进行标准化处理。

from pyspark import SparkContext
from pyspark.sql import SQLContext

# 初始化SparkContext和SQLContext
sc = SparkContext()
sqlContext = SQLContext(sc)

# 创建Spark DataFrame
data_rdd = sc.parallelize(data)
data_df = sqlContext.createDataFrame(data_rdd, ['value'])

# 计算全局均值和标准差
global_mean = data_df.agg({"value": "mean"}).collect()[0][0]
global_std_dev = data_df.agg({"value": "stddev"}).collect()[0][0]

# 分发全局统计信息
broadcasted_mean = sc.broadcast(global_mean)
broadcasted_std_dev = sc.broadcast(global_std_dev)

# 在每个节点上标准化数据
z_score_data = data_df.rdd.map(lambda row: (row['value'] - broadcasted_mean.value) / broadcasted_std_dev.value)

# 收集处理后的数据
z_score_data.collect()

在这一章节中，我们介绍了Z-Score方法的高级应用，从统计学理论的深入理解，到非参数方法的结合，再到大数据环境下的优化策略。这些内容展示了Z-Score作为一个数据分析工具的灵活性和强大功能。通过结合其他技术和方法，Z-Score能够更好地适应复杂的现实世界数据处理需求。

# 5. Z-Score方法的未来发展方向

随着人工智能和机器学习技术的快速发展，数据预处理方法也在不断进化。作为数据预处理中的一种重要手段，Z-Score方法的未来发展不仅关乎其自身的优化与改进，也与深度学习等新兴技术的融合息息相关。本章节将探讨Z-Score在深度学习中的潜在应用以及未来可能面临的挑战和研究方向。

## 5.1 Z-Score在深度学习中的潜在应用

深度学习模型的性能高度依赖于输入数据的质量。Z-Score作为一种有效的数据标准化方法，可以帮助提高深度学习模型训练的效率和性能。

### 5.1.1 深度学习对数据预处理的要求

在深度学习中，数据预处理是至关重要的一个步骤。模型需要从标准化的数据中学习特征的模式，以提高收敛速度和模型泛化能力。深度学习对数据预处理的要求包括但不限于：

- 数据的规模和质量
- 特征值的标准化处理
- 处理缺失值和异常值

深度学习模型对于输入数据的标准化非常敏感，因为网络权重的初始化和更新依赖于输入数据的分布。如果数据没有进行合适的预处理，可能导致模型训练效率低下或性能不佳。

### 5.1.2 Z-Score与其他深度学习技术的融合探讨

将Z-Score与深度学习技术结合，可以为模型提供一个更加稳定和有效的训练过程。例如，在训练循环神经网络（RNN）时，如果输入数据在不同的时间步长上具有不同的尺度，那么可以先使用Z-Score标准化来确保时间序列数据的平稳性。再比如，在卷积神经网络（CNN）的输入图像预处理中，Z-Score也可以帮助减少不同特征维度的尺度差异。

此外，Z-Score还可以与自动编码器（Autoencoder）等无监督学习模型结合，用于特征提取和降维，以此来改善网络的学习性能和计算效率。

## 5.2 未来研究方向与挑战

Z-Score方法作为数据预处理的一个重要工具，其未来的研究方向和挑战与数据科学的发展紧密相连。

### 5.2.1 Z-Score方法面临的新兴挑战

在实际应用中，Z-Score方法仍然面临一些挑战：

- 非高斯分布数据的处理：对于非高斯分布的数据集，Z-Score标准化可能不会产生理想的效果，需要进一步研究更适应这类数据的标准化方法。
- 自动化和智能化：如何实现Z-Score标准化的自动化，甚至智能化调整其参数，以适应不同数据集的特点，是当前研究中的一个难点。

### 5.2.2 对Z-Score方法未来发展的展望

尽管面临挑战，Z-Score方法的未来发展仍然值得期待：

- 结合新兴的机器学习算法：随着机器学习领域新算法的不断涌现，Z-Score也可以和其他算法相结合，实现更为复杂的场景下的应用。
- 在大数据和云平台中的应用：随着大数据技术的发展，如何在云计算环境中高效地实施Z-Score标准化，以及如何处理大规模数据集上的特征缩放问题，将是未来的一个研究重点。

综上所述，Z-Score方法在未来的发展前景广阔，但同时也需要我们不断创新和解决实际应用中的新问题。随着技术的进步，Z-Score方法将会在数据预处理领域继续扮演着重要的角色。