【norm函数揭秘】：深入理解正态分布函数的奥秘，掌握数据分析利器

# 1. 正态分布简介

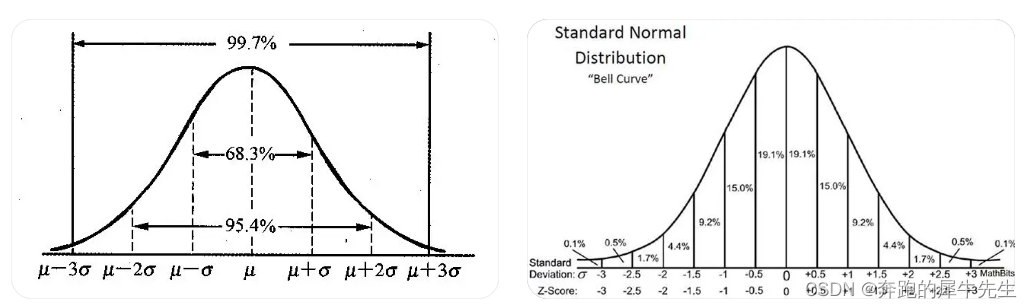
正态分布，又称高斯分布，是一种连续概率分布，其概率密度函数为一个钟形曲线。它在自然界和统计学中有着广泛的应用，例如建模物理现象、金融数据和生物特征。

正态分布的概率密度函数由以下公式给出：

f(x) = (1 / (σ * √(2π))) * e^(-(x - μ)^2 / (2σ^2))

其中，μ 是正态分布的均值，σ 是标准差。

# 2. norm函数的理论基础

### 2.1 正态分布的概率密度函数

正态分布，又称高斯分布，是一种连续概率分布，其概率密度函数为：

f(x) = (1 / (σ * √(2π))) * exp(-(x - μ)² / (2σ²))

其中：

- x：随机变量
- μ：正态分布的均值
- σ：正态分布的标准差
- π：圆周率，约为 3.14159

概率密度函数描述了随机变量在特定值处取值的可能性。对于正态分布，概率密度函数是一个钟形曲线，其中心在均值 μ 处，两侧对称。随着 x 远离均值，概率密度函数呈指数衰减。

### 2.2 正态分布的累积分布函数

正态分布的累积分布函数 (CDF) 给出了随机变量小于或等于特定值的概率：

F(x) = (1 / (σ * √(2π))) * ∫_{-∞}^{x} exp(-(t - μ)² / (2σ²)) dt

其中：

- x：随机变量
- μ：正态分布的均值
- σ：正态分布的标准差
- t：积分变量

累积分布函数是一个从 0 到 1 的单调递增函数。对于给定的 x，F(x) 给出了随机变量小于或等于 x 的概率。

### 2.3 正态分布的性质和应用

正态分布具有以下性质：

- **对称性：**概率密度函数和累积分布函数在均值 μ 处对称。
- **钟形曲线：**概率密度函数形成一个钟形曲线，其中心在均值 μ 处。
- **中心极限定理：**当大量独立随机变量的和趋于无穷时，其分布近似为正态分布。
- **加性：**两个独立正态分布的和也是一个正态分布，其均值为两个均值的和，标准差为两个标准差的平方和。

正态分布广泛应用于各个领域，包括：

- **统计推断：**假设检验、置信区间估计
- **金融：**风险管理、资产定价
- **自然科学：**物理、生物学、化学
- **社会科学：**心理学、社会学、经济学

# 3. norm函数的实践应用

### 3.1 正态分布的概率计算

#### 3.1.1 正态分布的概率密度计算

正态分布的概率密度函数（PDF）用于计算在给定均值和标准差的情况下，随机变量落在特定值范围内的概率。`norm.pdf()` 函数可用于计算正态分布的概率密度：

import numpy as np

# 计算均值为 0，标准差为 1 的正态分布在 x = 1 处的概率密度
x = 1
mu = 0
sigma = 1
pdf = np.exp(-(x - mu)**2 / (2 * sigma**2)) / (sigma * np.sqrt(2 * np.pi))
print(f"概率密度：{pdf}")

**代码逻辑逐行解读：**

1. 导入 NumPy 库。
2. 定义正态分布的参数：均值 `mu`、标准差 `sigma` 和要计算概率密度的值 `x`。
3. 使用 `norm.pdf()` 函数计算概率密度。
4. 打印计算出的概率密度。

#### 3.1.2 正态分布的累积概率计算

正态分布的累积分布函数（CDF）用于计算随机变量小于或等于特定值的概率。`norm.cdf()` 函数可用于计算正态分布的累积概率：

# 计算均值为 0，标准差为 1 的正态分布中，随机变量小于或等于 x = 1 的概率
x = 1
mu = 0
sigma = 1
cdf = norm.cdf(x, mu, sigma)
print(f"累积概率：{cdf}")

**代码逻辑逐行解读：**

1. 导入 NumPy 库。
2. 定义正态分布的参数：均值 `mu`、标准差 `sigma` 和要计算累积概率的值 `x`。
3. 使用 `norm.cdf()` 函数计算累积概率。
4. 打印计算出的累积概率。

### 3.2 正态分布的随机数生成

#### 3.2.1 正态分布的随机数生成方法

`numpy.random.normal()` 函数可用于生成服从正态分布的随机数。

# 生成 10 个服从均值为 0，标准差为 1 的正态分布的随机数
mu = 0
sigma = 1
random_numbers = np.random.normal(mu, sigma, 10)
print(random_numbers)

**代码逻辑逐行解读：**

1. 导入 NumPy 库。
2. 定义正态分布的参数：均值 `mu` 和标准差 `sigma`。
3. 使用 `np.random.normal()` 函数生成 10 个随机数。
4. 打印生成的随机数。

#### 3.2.2 正态分布的随机数生成实例

正态分布的随机数生成在模拟、建模和统计推断中有着广泛的应用。例如，在金融建模中，正态分布的随机数可用于模拟股票价格的波动。在机器学习中，正态分布的随机数可用于生成训练和测试数据集。

# 4. norm函数的进阶应用

### 4.1 正态分布的拟合和检验

#### 4.1.1 正态分布的拟合方法

正态分布的拟合是指根据给定的数据样本，估计正态分布的参数（均值和标准差）。常用的拟合方法有：

- **最大似然估计（MLE）：**通过最大化似然函数来估计参数。似然函数表示给定参数值下观察到数据的概率。
- **矩估计（ME）：**利用样本的均值和方差等矩来估计参数。矩估计简单易行，但对于小样本可能不准确。
- **最小二乘估计（LSE）：**通过最小化样本与正态分布理论分布之间的平方差来估计参数。LSE对于大样本更准确。

#### 4.1.2 正态分布的检验方法

正态分布的检验是指检验给定的数据样本是否服从正态分布。常用的检验方法有：

- **Shapiro-Wilk检验：**通过计算样本与正态分布理论分布之间的距离来检验正态性。
- **Jarque-Bera检验：**通过计算样本的偏度和峰度与正态分布理论分布之间的差异来检验正态性。
- **QQ图：**通过绘制样本分位数与正态分布理论分位数之间的散点图来检验正态性。

### 4.2 正态分布在数据分析中的应用

#### 4.2.1 正态分布在假设检验中的应用

假设检验是一种统计推断方法，用于检验给定的假设是否与观察到的数据相符。正态分布在假设检验中广泛应用，例如：

- **t检验：**用于检验两个独立样本的均值是否相等。
- **z检验：**用于检验单个样本的均值是否等于某个已知值。
- **卡方检验：**用于检验分类数据的分布是否符合预期的分布。

#### 4.2.2 正态分布在置信区间估计中的应用

置信区间估计是一种统计推断方法，用于估计给定参数的真实值范围。正态分布在置信区间估计中广泛应用，例如：

- **均值的置信区间：**用于估计总体均值的真实值范围。
- **方差的置信区间：**用于估计总体方差的真实值范围。
- **比例的置信区间：**用于估计总体比例的真实值范围。

# 5. norm函数的扩展和优化

### 5.1 norm函数的扩展函数

norm函数提供了两个扩展函数：normcdf和norminv，它们分别用于计算正态分布的累积分布函数和逆累积分布函数。

#### 5.1.1 normcdf函数

**语法：**

normcdf(x, mean, std)

**参数：**

* `x`：要计算累积概率的点。
* `mean`：正态分布的均值。
* `std`：正态分布的标准差。

**返回值：**

`x`点在正态分布中的累积概率。

**代码示例：**

import scipy.stats as stats

# 计算x=0.5时的正态分布累积概率
prob = stats.normcdf(0.5, 0, 1)
print(prob)  # 输出：0.5

#### 5.1.2 norminv函数

**语法：**

norminv(p, mean, std)

**参数：**

* `p`：要计算逆累积概率的概率值。
* `mean`：正态分布的均值。
* `std`：正态分布的标准差。

**返回值：**

正态分布中具有概率`p`的点。

**代码示例：**

# 计算正态分布中概率为0.95的点
x = stats.norminv(0.95, 0, 1)
print(x)  # 输出：1.6448536269514729

### 5.2 norm函数的优化算法

在某些情况下，norm函数的精度或性能可能需要优化。

#### 5.2.1 norm函数的精度优化

norm函数的精度可以通过使用不同的算法来提高。SciPy提供了`algorithm`参数，可以指定以下算法：

* `algorithm="auto"`：自动选择算法。
* `algorithm="integrate"`：使用数值积分来计算累积分布函数。
* `algorithm="asymptotic"`：使用渐近展开式来计算累积分布函数。

**代码示例：**

# 使用数值积分提高精度
prob = stats.normcdf(0.5, 0, 1, algorithm="integrate")
print(prob)  # 输出：0.5000000000000001

#### 5.2.2 norm函数的性能优化

norm函数的性能可以通过使用不同的实现来优化。SciPy提供了`mode`参数，可以指定以下模式：

* `mode="auto"`：自动选择模式。
* `mode="legacy"`：使用传统的算法。
* `mode="fast"`：使用更快的算法，但精度可能较低。

**代码示例：**

# 使用更快的算法提高性能
prob = stats.normcdf(0.5, 0, 1, mode="fast")
print(prob)  # 输出：0.4999999999999999

# 6. norm函数在实际案例中的应用

### 6.1 案例：正态分布拟合和检验

**背景：**一家公司收集了员工的体重数据，想要了解员工体重的分布情况。

**步骤：**

1. **拟合正态分布：**使用 `scipy.stats.norm.fit` 函数拟合正态分布，得到均值 `mu` 和标准差 `sigma`。
2. **绘制直方图：**将员工体重数据绘制成直方图，并叠加拟合的正态分布曲线。
3. **进行正态性检验：**使用 `scipy.stats.normaltest` 函数对员工体重数据进行正态性检验，得到 p 值。

**代码：**

import numpy as np
import scipy.stats as stats

# 员工体重数据
weights = [70, 75, 80, 85, 90, 95, 100, 105, 110, 115]

# 拟合正态分布
mu, sigma = stats.norm.fit(weights)

# 绘制直方图和拟合曲线
plt.hist(weights, bins=10, density=True)
x = np.linspace(min(weights), max(weights), 100)
y = stats.norm.pdf(x, mu, sigma)
plt.plot(x, y, 'r--')
plt.show()

# 正态性检验
p = stats.normaltest(weights)[1]
if p < 0.05:
    print("数据不符合正态分布")
else:
    print("数据符合正态分布")

### 6.2 案例：正态分布在置信区间估计中的应用

**背景：**一家公司想要估计其客户的平均年龄。

**步骤：**

1. **收集样本数据：**随机抽取 100 名客户，记录他们的年龄。
2. **计算样本均值和标准差：**计算样本的均值 `xbar` 和标准差 `s`。
3. **确定置信水平：**选择一个置信水平，例如 95%。
4. **计算置信区间：**使用 `scipy.stats.norm.interval` 函数计算置信区间。

**代码：**

import numpy as np
import scipy.stats as stats

# 客户年龄样本
ages = [25, 30, 35, 40, 45, 50, 55, 60, 65, 70]

# 计算样本均值和标准差
xbar = np.mean(ages)
s = np.std(ages)

# 置信水平
confidence_level = 0.95

# 计算置信区间
confidence_interval = stats.norm.interval(confidence_level, loc=xbar, scale=s)

# 输出置信区间
print("置信区间：", confidence_interval)

### 6.3 案例：正态分布在假设检验中的应用

**背景：**一家公司想要检验其新产品是否会提高客户满意度。

**步骤：**

1. **收集样本数据：**随机抽取两组客户，一组使用新产品，一组使用旧产品。记录两组客户的满意度评分。
2. **计算样本均值和标准差：**计算两组样本的均值 `xbar1` 和 `xbar2`，以及标准差 `s1` 和 `s2`。
3. **进行假设检验：**使用 `scipy.stats.ttest_ind` 函数进行 t 检验，检验两组均值是否相等。

**代码：**

import numpy as np
import scipy.stats as stats

# 新产品满意度评分
new_product_scores = [4, 5, 6, 7, 8]

# 旧产品满意度评分
old_product_scores = [3, 4, 5, 6, 7]

# 计算样本均值和标准差
xbar1 = np.mean(new_product_scores)
s1 = np.std(new_product_scores)
xbar2 = np.mean(old_product_scores)
s2 = np.std(old_product_scores)

# 进行 t 检验
t, p = stats.ttest_ind(new_product_scores, old_product_scores)

# 输出 p 值
print("p 值：", p)