norm函数与正态分布：揭示数据背后的规律，探索统计世界的奥秘

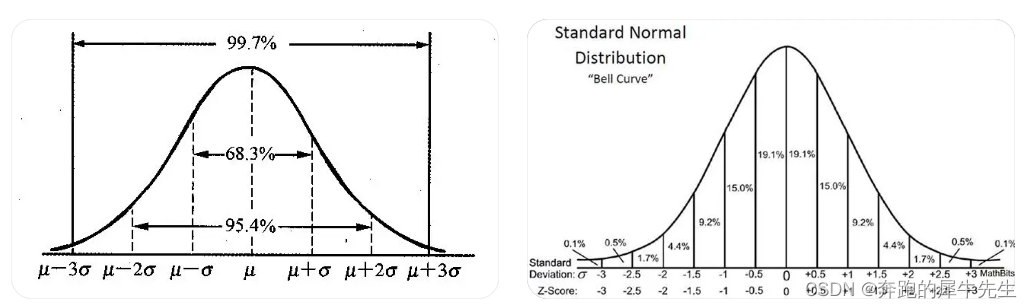
# 1. 正态分布的理论基础

正态分布，又称高斯分布，是概率论中最重要的连续概率分布之一。它广泛应用于自然科学、社会科学和工程技术等领域。

正态分布的概率密度函数为：

f(x) = (1 / (σ * √(2π))) * e^(-(x - μ)² / (2σ²))

其中：

- μ：正态分布的均值
- σ：正态分布的标准差
- π：圆周率

正态分布具有以下特性：

- **对称性：**正态分布的概率密度函数关于均值μ对称。
- **钟形曲线：**正态分布的概率密度函数呈钟形曲线，其峰值位于均值μ处。
- **渐近性：**随着x与μ的距离增加，正态分布的概率密度函数会迅速减小，趋近于0。

# 2. norm函数的应用与实现

### 2.1 norm函数的语法和参数

#### 2.1.1 norm函数的定义

norm函数用于计算正态分布的概率密度函数或累积分布函数。其语法格式如下：

scipy.stats.norm.pdf(x, loc=0, scale=1)
scipy.stats.norm.cdf(x, loc=0, scale=1)

其中：

* `x`：要计算的点的值。
* `loc`：正态分布的均值（默认值为0）。
* `scale`：正态分布的标准差（默认值为1）。

#### 2.1.2 norm函数的参数详解

norm函数的参数包括：

| 参数 | 描述 |
|---|---|
| `x` | 要计算的点的值。 |
| `loc` | 正态分布的均值。 |
| `scale` | 正态分布的标准差。 |
| `cumulative` | 是否计算累积分布函数（默认为False）。 |
| `maxpts` | 数值积分的最大积分点数（默认为200）。 |

### 2.2 norm函数的应用场景

norm函数广泛应用于各种领域，包括：

#### 2.2.1 数据分布的拟合

norm函数可以用来拟合数据分布，确定数据的正态性。通过比较数据分布与正态分布的拟合程度，可以判断数据是否符合正态分布。

#### 2.2.2 概率计算

norm函数可以用来计算正态分布的概率，包括：

* **概率密度函数：**计算给定点处正态分布的概率密度。
* **累积分布函数：**计算小于或等于给定点的正态分布的概率。

### 2.3 norm函数的实现原理

norm函数的实现原理主要涉及以下两个方面：

#### 2.3.1 概率密度函数的推导

正态分布的概率密度函数为：

f(x) = (1 / (σ√(2π))) * e^(-(x-μ)² / (2σ²))

其中：

* μ：正态分布的均值
* σ：正态分布的标准差

#### 2.3.2 数值积分方法

norm函数使用数值积分方法来计算累积分布函数。常用的数值积分方法包括：

* **梯形法则：**将积分区间划分为等宽的子区间，并用子区间内函数值的梯形面积近似积分值。
* **辛普森法则：**将积分区间划分为等宽的子区间，并用子区间内函数值的抛物线面积近似积分值。

通过使用数值积分方法，可以将累积分布函数的计算转化为有限次函数值的求和。

# 3.1 数据分析与建模