norm函数与其他分布函数的比较：探索正态分布的独特之处，掌握数据分布规律

# 1. 概率分布概述

概率分布是描述随机变量取值可能性的数学模型。它指定了随机变量在不同取值上的概率。概率分布广泛应用于统计、机器学习和金融等领域。

概率分布的类型有很多，其中正态分布是最重要的分布之一。正态分布又称高斯分布，其概率密度函数呈钟形曲线。正态分布在自然界和社会科学中广泛存在，例如身高、体重和测量误差等。

# 2. 正态分布的理论基础

### 2.1 正态分布的定义和性质

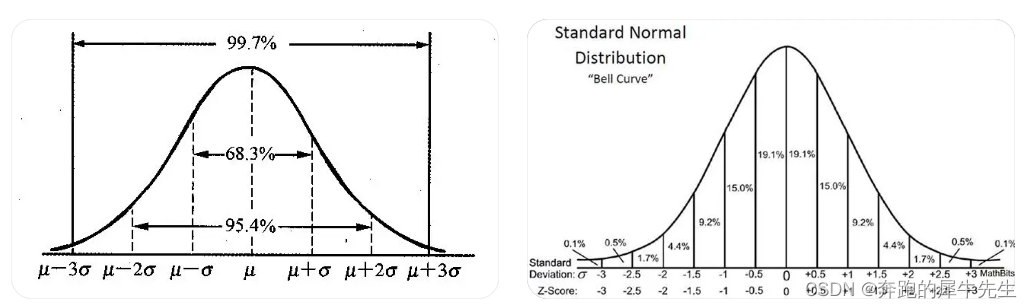
正态分布，也称为高斯分布，是一种连续概率分布，其概率密度函数呈钟形曲线。它具有以下几个关键性质：

- **对称性：**正态分布的概率密度函数关于其均值对称。
- **单峰性：**正态分布的概率密度函数只有一个峰值，位于均值处。
- **渐近性：**正态分布的概率密度函数在均值两侧呈渐近衰减。

### 2.2 正态分布的概率密度函数

正态分布的概率密度函数由以下公式给出：

f(x) = (1 / (σ√(2π))) * e^(-(x - μ)² / (2σ²))

其中：

- `x` 是随机变量
- `μ` 是正态分布的均值
- `σ` 是正态分布的标准差

### 2.3 正态分布的累积分布函数

正态分布的累积分布函数 (CDF) 给出了随机变量小于或等于特定值的概率。CDF 由以下公式给出：

F(x) = (1 / 2) * (1 + erf((x - μ) / (σ√(2))))

其中：

- `erf` 是误差函数

**代码块逻辑分析：**

该代码块计算了正态分布的累积分布函数。`erf` 函数计算误差函数，其值为正态分布中小于或等于指定值的概率。

**参数说明：**

- `x`：随机变量
- `μ`：正态分布的均值
- `σ`：正态分布的标准差

### 2.4 正态分布的标准化

正态分布可以通过以下公式标准化：

z = (x - μ) / σ

其中：

- `z` 是标准正态分布的随机变量
- `x` 是正态分布的随机变量
- `μ` 是正态分布的均值
- `σ` 是正态分布的标准差

**代码块逻辑分析：**

该代码块将正态分布随机变量标准化为标准正态分布。标准正态分布的均值为 0，标准差为 1。

**参数说明：**

- `x`：正态分布的随机变量
- `μ`：正态分布的均值
- `σ`：正态分布的标准差

# 3.1 正态分布在统计推断中的应用

正态分布在统计推断中扮演着至关重要的角色，它为我们提供了对总体参数进行推断的基础。

#### 置信区间估计

置信区间估计是统计推断中常用的方法，它可以帮助我们估计总体参数的真实值落在某个范围内的概率。正态分布的概率密度函数和累积分布函数为我们提供了构建置信区间的理论基础。

假设我们有一个样本，其样本均值和样本标准差分别为 $\bar{x}$ 和 $s$，则总体均值 $\mu$ 的置信区间为：

import scipy.stats as stats

# 置信水平
confidence_level = 0.95

# 计算置信区间
z_score = stats.norm.ppf(1 - (1 - confidence_level) / 2)
margin_of_error = z_score * s / np.sqrt(n)
lower_bound = np.mean(sample) - margin_of_error
upper_bound = np.mean(sample) + margin_of_error

print("置信区间：", lower_bound, upper_bound)

#### 假设检验

假设检验是另一种重要的统计推断方法，它用于检验有关总体参