【CNN可视化技术】：揭秘模型是如何看和理解图像的

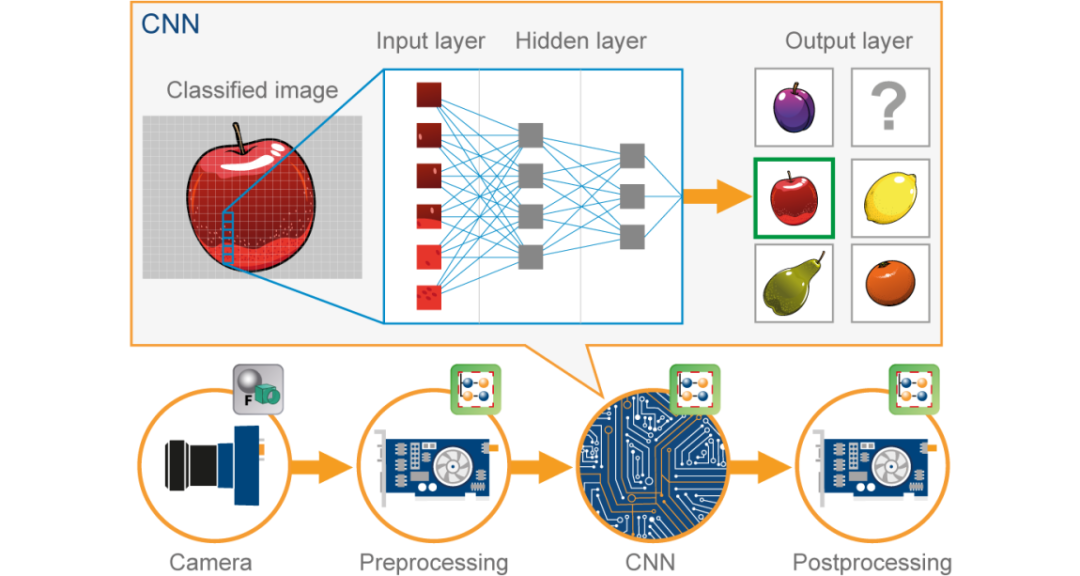
# 1. CNN可视化技术概述

## 1.1 CNN可视化的意义与背景

在深度学习领域，卷积神经网络（CNN）已成为图像识别和处理的关键技术。CNN的黑盒特性，使得模型内部的处理过程对研究者和开发者不透明。因此，CNN可视化技术应运而生，旨在通过直观展示网络内部机制，提升模型的可解释性，进而优化模型性能、减少误判，并为后续研究提供参考。本章将对CNN可视化技术进行概述，解释其背后的意义以及在深度学习中的重要性。

## 1.2 可视化的种类与方法

CNN可视化技术主要分为两类：模型内部状态的可视化和输入数据变化下的模型响应可视化。常见的内部状态可视化方法包括激活图、特征图和权重的可视化，而模型响应可视化则更多关注数据处理过程，例如梯度上升或下降过程中的变化。此外，还有类激活映射（CAM）和注意力机制等技术，通过突出特定区域来揭示模型决策的关键因素。

## 1.3 可视化技术的应用场景

CNN可视化技术在多个领域发挥着重要作用，如故障诊断、模型改进、知识提取以及教育和研究。通过可视化，可以帮助研究人员理解模型在特定数据集上的表现，为模型调试和优化提供直观依据。同时，可视化技术也使得深度学习模型的决策过程更为透明，增强了用户对模型的信任度，并为非专业人员提供了一种理解和解读复杂模型的方式。

flowchart LR
    A[应用CNN可视化技术] --> B[提高模型可解释性]
    B --> C[优化模型性能]
    B --> D[减少误判]
    B --> E[为研究提供参考]
    C --> F[模型改进]
    D --> F
    E --> G[增强信任度]
    E --> H[简化模型理解]

在接下来的章节中，我们将深入探讨CNN的基础理论，实践方法以及未来趋势和挑战，以提供更全面的CNN可视化技术图景。

# 2. 卷积神经网络的基础理论

### 2.1 CNN的结构和工作原理
#### 2.1.1 卷积层的作用和计算
卷积层是卷积神经网络（CNN）的核心组成部分之一，它通过卷积操作提取输入数据的局部特征。在图像处理领域，卷积层可以识别边缘、角点等基本视觉模式。卷积操作涉及一个卷积核（滤波器）和输入数据之间的数学运算。

卷积运算的基本过程可以总结为以下步骤：

1. **初始化卷积核**：卷积核是一个小的矩阵，其维度通常远小于输入数据的维度，且所有元素初始值通常由高斯分布或其他方式随机生成。

2. **卷积核滑动**：将卷积核从输入数据的左上角开始，按照一定的步长（stride）在输入数据上滑动。每次移动覆盖输入数据的一个窗口，并在该窗口内执行元素乘累加操作。

3. **执行卷积计算**：在卷积核覆盖的输入数据窗口内，将卷积核中的每个元素与其对应位置的输入数据相乘，并将结果相加。得到的单一值作为输出数据的一个元素。

4. **产生特征图**：通过移动卷积核，对输入数据的每个区域重复上述过程，最终得到一个二维的特征图（feature map），其中每个元素都是对输入数据的一个局部区域的响应。

以下是该过程的简单数学表示：

假设输入数据为 \(X\)，卷积核为 \(K\)，输出特征图为 \(Y\)，则特征图中的每个元素 \(Y[i, j]\) 可以通过下列公式计算：

\[ Y[i, j] = (K * X)[i, j] = \sum_m \sum_n K[m, n] \cdot X[i + m, j + n] \]

这里，\(i\) 和 \(j\) 表示输出特征图中元素的位置索引，\(m\) 和 \(n\) 表示卷积核的索引。

代码块示例：

import numpy as np

def convolve2d(image, kernel):
    # image is a numpy array of shape (height, width)
    # kernel is a numpy array of shape (kernel_height, kernel_width)
    kernel_height, kernel_width = kernel.shape
    output_height, output_width = image.shape[0] - kernel_height + 1, image.shape[1] - kernel_width + 1
    # Initialize the output feature map
    feature_map = np.zeros((output_height, output_width))
    # Perform the convolution
    for y in range(output_height):
        for x in range(output_width):
            feature_map[y, x] = np.sum(kernel * image[y:y + kernel_height, x:x + kernel_width])
    return feature_map

# Example usage:
image = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
kernel = np.array([[0, -1, 0], [-1, 4, -1], [0, -1, 0]])
feature_map = convolve2d(image, kernel)
print("Feature map:\n", feature_map)

执行逻辑说明：上述代码中定义了一个二维卷积函数 `convolve2d`，它接受一个图像矩阵和一个卷积核作为输入，然后计算卷积核覆盖的图像区域的元素乘累加和，产生一个特征图。在这个例子中，我们使用了一个边缘检测核对图像进行卷积，得到的特征图突出显示了图像的边缘。

参数说明：代码中的 `image` 和 `kernel` 参数分别代表输入图像和卷积核，它们都是二维的NumPy数组。通过调整卷积核的大小和值，可以提取图像的不同特征。

#### 2.1.2 池化层的功能与影响
池化层（Pooling Layer）是CNN中用于降低特征图空间维度的结构，它通过下采样操作来减少参数数量和计算量，进而减少过拟合的风险。常见的池化操作包括最大池化（Max Pooling）和平均池化（Average Pooling）。

最大池化通过选取局部区域内的最大值作为输出，这有助于提取图像的特征并保持其在空间位置上的不变性，这对于物体检测和识别等任务特别重要。

平均池化则是将局部区域内的所有值求平均后作为输出，这有助于滤除噪声并实现平滑，但相对于最大池化，可能会丢失一些特征信息。

池化层的工作原理如下：

1. **定义池化区域**：首先确定池化操作的局部区域大小（池化窗口大小）和步长。

2. **应用池化函数**：在每个局部区域上应用池化函数。在最大池化的情况下，选择该区域的最大值；在平均池化的情况下，计算该区域的平均值。

3. **输出结果**：池化后的结果将构成一个新的特征图，其维度较小，但保留了重要的特征信息。

池化操作的示例代码块：

def max_pooling(feature_map, pool_size=2, stride=2):
    # feature_map is a numpy array of shape (height, width)
    input_height, input_width = feature_map.shape
    output_height = input_height // stride
    output_width = input_width // stride
    # Initialize the output feature map
    pooled_feature_map = np.zeros((output_height, output_width))
    # Perform max pooling
    for y in range(0, output_height):
        for x in range(0, output_width):
            # Select the pooling region
            region = feature_map[y * stride:(y + 1) * stride, x * stride:(x + 1) * stride]
            # Apply max pooling
            pooled_feature_map[y, x] = np.max(region)
    return pooled_feature_map

# Example usage:
feature_map = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [13, 14, 15, 16]])
pooled_feature_map = max_pooling(feature_map)
print("Max-pooled Feature Map:\n", pooled_feature_map)

执行逻辑说明：该代码定义了一个最大池化函数 `max_pooling`，它接受一个特征图作为输入，并通过选取局部区域的最大值来实现最大池化。在这个例子中，我们使用了一个2x2的池化窗口和步长2对特征图进行下采样，得到输出特征图。

参数说明：`feature_map` 是输入的特征图，`pool_size` 定义了池化窗口的大小，`stride` 表示池化窗口的移动步长。通过调整这些参数，可以控制池化层的降维程度以及对特征图的空间不变性的保持。

#### 2.1.3 全连接层的角色和重要性
全连接层（Fully Connected Layer，简称FC层）位于CNN的末端，是网络中用于将学习到的特征映射到最终输出结果的关键部分。不同于卷积层和池化层专注于局部特征的提取，全连接层负责整合所有从卷积层和池化层中提取的特征，并进行分类或其他任务的决策。

全连接层的工作机制较为简单：

1. **特征展平**：在网络的最后，所有通过卷积层和池化层提取的多维特征图需要被展平（Flatten）成一维数组，以便输入到全连接层。

2. **权重与偏置**：全连接层拥有权重矩阵和偏置向量，它们在训练过程中通过反向传播算法学习调整。

3. **线性变换和非线性激活**：特征展平后，通过矩阵乘法与权重矩阵相乘，再加上偏置向量，得到线性变换结果。通常在这之后会应用一个非线性激活函数，如ReLU，以引入非线性，帮助网络学习复杂的模式。

全连接层的数学表示如下：

假设展平后的特征向量为 \(X\)，权重矩阵为 \(W\)，偏置向量为 \(b\)，输出向量为 \(Y\)，则全连接层的计算可以表示为：

\[ Y = \text{activation}(XW + b) \]

其中 `activation` 是激活函数。

示例代码块：

def fully_connected(input_vector, weights, biases):
    # input_vector is a numpy array of shape (features,)
    # weights is a numpy array of shape (features, classes)
    # biases is a numpy array of shape (classes,)
    # The output is the prediction vector of shape (classes,)
    output =