【损失函数选择】：卷积神经网络中损失函数的优化策略

# 1. 卷积神经网络与损失函数

## 1.1 神经网络的基本概念
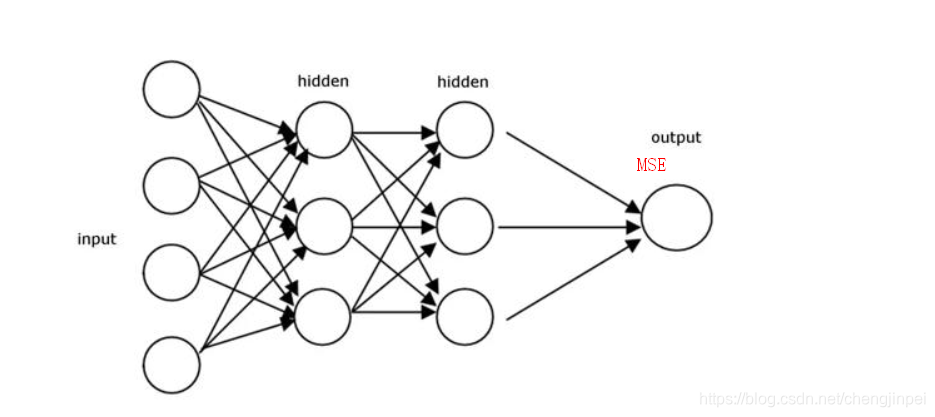
在深度学习领域，卷积神经网络（CNN）是最成功的应用之一，特别是在图像识别和分类任务中。CNN通过自动学习图像的层次特征，实现高效的模式识别。然而，CNN的成功不仅取决于其结构，还有赖于一个关键组件——损失函数。损失函数衡量的是模型预测值与真实值之间的差距，是模型优化的核心目标。

## 1.2 损失函数的作用与重要性
损失函数，在CNN中扮演着指导模型学习的角色。它的选择直接影响到模型训练的效率和结果的质量。好的损失函数能够使模型更准确地捕捉数据的分布特性，快速收敛至最优解。因此，理解不同类型的损失函数及其适用场景，对于构建高性能的CNN模型至关重要。

## 1.3 常见的卷积神经网络损失函数
在卷积神经网络中，常用的损失函数包括均方误差（MSE）对于回归任务，交叉熵损失函数（Cross-Entropy Loss）则广泛应用于分类任务。交叉熵损失函数通过衡量模型输出的概率分布与实际标签的概率分布之间的差异，促进了模型在分类问题上的快速学习。下一章节我们将进一步探讨损失函数的理论基础及其数学原理。

# 2. 损失函数的理论基础

### 2.1 损失函数的定义与分类
#### 2.1.1 损失函数的基本概念
损失函数（Loss Function），在机器学习尤其是深度学习中，是衡量模型预测值和真实值之间差异的函数。它是优化算法的核心，用于指导模型参数的调整，以达到最小化模型预测错误的目的。损失函数通常与优化问题紧密相关，例如在回归问题中，损失函数可以计算预测值与真实值之间的差的平方和，在分类问题中，损失函数可以用来衡量模型预测概率分布与真实分布之间的差异。

基本概念中包含以下几个要点：
- **误差度量**：损失函数量化了预测结果的误差大小。
- **模型参数**：模型通过优化算法调节参数，以最小化损失函数。
- **优化目标**：损失函数的值越小，表示模型的预测越接近真实值。

#### 2.1.2 常见损失函数类型概述
在机器学习中，不同类型的模型和任务对应着不同的损失函数。以下是一些最常用的损失函数类型：

- **均方误差（MSE）**：常用于回归问题，计算预测值和真实值差的平方和。
- **交叉熵（Cross-Entropy）**：常用于分类问题，衡量两个概率分布之间的差异。
- **绝对误差（MAE）**：同样是回归问题中常用的损失函数，计算预测值和真实值之间差的绝对值。
- **对数损失（Log Loss）**：当预测值是概率分布时，该损失函数能够更好地处理分类问题。

每个损失函数都有其适用的场景和优缺点，选择合适的损失函数对模型的性能至关重要。

### 2.2 损失函数的数学原理
#### 2.2.1 损失函数的目标优化
损失函数的最小化是模型训练的核心目标。在实际操作中，我们通过梯度下降算法对损失函数进行优化。梯度下降算法通过计算损失函数关于模型参数的梯度，并用这个梯度来更新参数，从而使损失函数值下降。

数学表达为：
$$ \theta_{\text{new}} = \theta_{\text{old}} - \alpha \nabla_\theta \mathcal{L}(y, f_\theta(x)) $$
其中，$\theta_{\text{new}}$ 和 $\theta_{\text{old}}$ 分别表示更新后的和更新前的模型参数，$\alpha$ 为学习率，$\nabla_\theta \mathcal{L}$ 是损失函数相对于参数的梯度，$f_\theta(x)$ 表示模型预测函数，$y$ 是真实标签。

#### 2.2.2 损失函数与梯度下降
梯度下降法是通过计算损失函数关于参数的梯度来实现参数更新的。梯度反映了损失函数在参数空间中最陡峭上升的方向。因此，我们可以通过向梯度相反的方向移动参数，来达到损失函数下降的目的。

在实际应用中，会有多种梯度下降的变体，包括批量梯度下降（Batch Gradient Descent）、随机梯度下降（Stochastic Gradient Descent）、小批量梯度下降（Mini-batch Gradient Descent）等。不同的梯度下降方法各有优劣，适用于不同规模和特性的数据集。

### 2.3 损失函数的选择标准
#### 2.3.1 任务相关性
损失函数的选择应该与具体的学习任务紧密相关。对于分类任务，交叉熵损失函数通常是首选，因为它能够有效反映概率分布的差异。对于回归任务，均方误差或者绝对误差可能更为合适。在一些特定的任务中，如序列生成、图像分割等，还需要根据任务特性自定义损失函数。

选择合适的损失函数需要深入理解任务的目标和数据的特性。例如，在处理不平衡分类问题时，可能会选择加权的交叉熵损失函数，以便给少数类更高的权重。

#### 2.3.2 损失函数的平衡性
损失函数的平衡性意味着模型在不同类别上的表现应保持一致。在多类分类问题中，由于类别间可能存在数量上的不平衡，使用未加权的损失函数可能会导致模型倾向于预测多数类，而忽视少数类。

为了解决这个问题，可以采用加权的损失函数，给少数类更高的权重。或者采用一种称为焦点损失（Focal Loss）的方法，通过减少易分类样本的权重，而增加难分类样本的权重，从而提高模型对少数类的关注。

#### 表格：不同任务类型对应的损失函数选择
| 任务类型 | 常用损失函数 |
|------------|--------------|
| 二分类 | 交叉熵损失函数 |
| 多分类 | 交叉熵损失函数 |
| 回归 | 均方误差损失函数 |
| 不平衡分类 | 加权交叉熵损失函数 |
| 序列生成 | 序列到序列损失函数 |
| 图像分割 | 交叉熵损失函数 |

在选择损失函数时，需要综合考虑任务类型、数据特性以及模型的性能要求。适当的选择和调整损失函数可以显著提升模型的训练效率和预测准确性。

# 3. 卷积神经网络损失函数的实践应用

## 3.1 分类任务中的损失函数

在卷积神经网络（CNN）的应用中，分类任务是核心之一。而在分类任务中，选择合适的损失函数对模型性能有着决定性的影响。我们将详细介绍在分类任务中常用的两种损失函数：交叉熵损失函数和对比损失函数。

### 3.1.1 交叉熵损失函数

交叉熵损失函数（Cross-Entropy Loss）是分类任务中最常用的损失函数之一，特别是在多类分类问题中。该函数衡量的是模型预测概率分布与真实概率分布之间的差异。在多分类问题中，交叉熵损失函数的一般形式为：

import tensorflow as tf
from tensorflow.keras.losses import CategoricalCrossentropy

# 假设 y_true 为真实的分类标签， y_pred 为模型的预测概率分布
loss_fn = CategoricalCrossentropy()
loss = loss_fn(y_true, y_pred)

交叉熵损失函数对错误分类的惩罚更大，它在模型预测概率与真实标签相去甚远时会产生较大的梯度，从而推动模型快速调整参数以减少预测误差。

### 3.1.2 对比损失函数

对比损失函数（Contrastive Loss）主要用于二分类问题，尤其适用于那些模型输出不是直接的类别概率，而是类别间距离的场景，比如孪生网络（Siamese Network）。对比损失函数的设计目标是使相同的类别之间的输出距离更近，不同的类别之间的输出距离更远。下面是一个简单的对比损失函数的代码实现示例：

import tensorflow as tf

def contrastive_loss(y_true, y_pred):
    # margin 为对比损失中距离的边界值
    margin = 1.0
    # 当输入标签为同一类时，公式变为半径为 margin 的圆，否则为超球体
    squared_pred = tf.square(y_pred)
    squared_true = tf.mult