双曲正切函数在回归问题中的应用：预测连续值的秘密武器

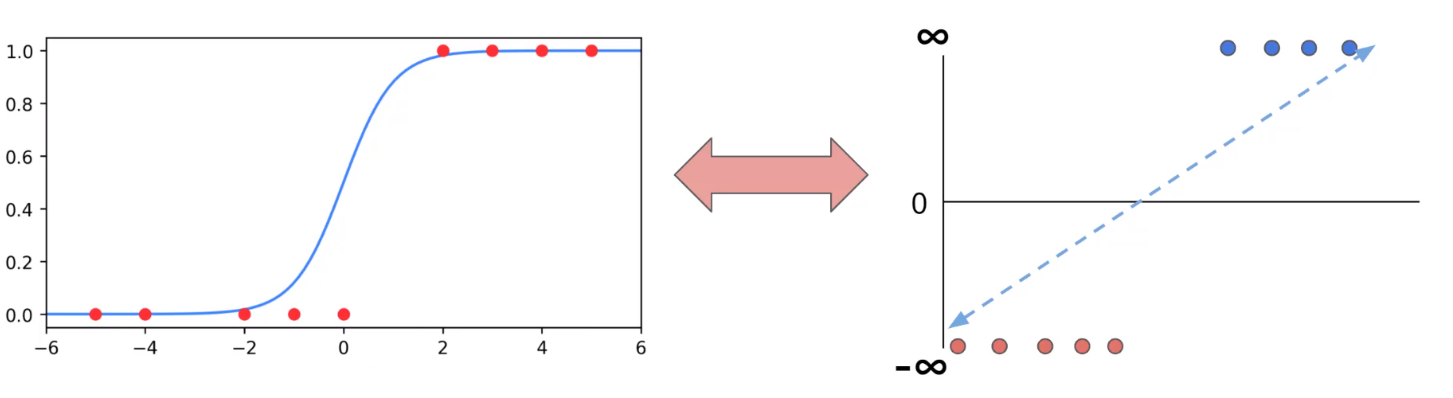
# 1. 双曲正切函数的理论基础**

双曲正切函数（tanh）是一种非线性函数，其数学表达式为：

tanh(x) = (e^x - e^(-x)) / (e^x + e^(-x))

它具有以下性质和特点：

- 取值范围为[-1, 1]，其中-1为渐近线，1为渐近线。
- 在原点对称，奇函数。
- 导数为：tanh'(x) = 1 - tanh^2(x)

# 2. 双曲正切函数在回归模型中的应用

双曲正切函数在回归模型中具有广泛的应用，它可以作为激活函数，引入非线性关系，提高模型的拟合能力。

### 2.1 线性回归模型中的双曲正切函数

#### 2.1.1 双曲正切函数的数学表达式

双曲正切函数的数学表达式为：

tanh(x) = (e^x - e^(-x)) / (e^x + e^(-x))

其中，x 为输入值。

#### 2.1.2 双曲正切函数的性质和特点

双曲正切函数具有以下性质和特点：

* **对称性：** tanh(-x) = -tanh(x)
* **范围：** tanh(x) 的取值范围为 (-1, 1)
* **单调性：** tanh(x) 在整个实数域上单调递增
* **导数：** tanh(x) 的导数为 sech^2(x)，其中 sech(x) = 1 / cosh(x)

### 2.2 逻辑回归模型中的双曲正切函数

#### 2.2.1 逻辑回归模型的原理

逻辑回归模型是一种二分类模型，用于预测一个二元变量（0 或 1）的概率。其数学表达式为：

p = 1 / (1 + e^(-(b0 + b1x)))

其中，p 为预测的概率，x 为输入值，b0 和 b1 为模型参数。

#### 2.2.2 双曲正切函数在逻辑回归中的作用

在逻辑回归模型中，双曲正切函数可以作为激活函数，将线性预测值转换为概率。具体来说，激活函数的表达式为：

tanh(b0 + b1x)

通过双曲正切函数的非线性变换，线性预测值被映射到 (0, 1) 范围内，从而得到预测的概率。

**代码示例：**

import numpy as np
import matplotlib.pyplot as plt

# 定义双曲正切函数
def tanh(x):
    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))

# 定义逻辑回归模型
def logistic_regression(x, b0, b1):
    return tanh(b0 + b1 * x)

# 训练数据
x = np.linspace(-5, 5, 100)
y = 1 / (1 + np.exp(-(0.5 + 0.2 * x)))

# 拟合模型
b0, b1 = np.polyfit(x, y, 1)

# 预测
y_pred = logistic_regression(x, b0, b1)

# 绘制图像
plt.plot(x, y, 'o')
plt.plot(x, y_pred, '-')
plt.show()

**代码逻辑分析：**

* `tanh` 函数定义了双曲正切函数的数学表达式。
* `logistic_regression` 函数定义了逻辑回归模型，其中双曲正切函数作为激活函数。
* `np.polyfit` 函数用于拟合模型参数。
* `y_pred` 存储了模型的预测值。
* `plt.plot` 函数绘制了真实值和预测值之间的关系。

**参数说明：**

* `x`：输入值
* `b0`：模型截距
* `b1`：模型斜率
* `y`：真实值
* `y_pred`：预测值

# 3. 双曲正切函数在回归模型中的实践

### 3.1 数据预处理和特征工程

在应用双曲正切函数进行回归建模之前，数据预处理和特征工程是至关重要的步骤，它们可以提高模型的性能和鲁棒性。

**3.1.1 数据标准化和归一化**

数据标准化和归一化是将数据特征的值域缩放到统一的范围内，以消除不同特征量纲的影响，提高模型的训练效率和收敛速度。

* **数据标准化：**将数据特征的值域缩放到均值为0，标准差为1的范围内。

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

* **数据归一化：**将数据特征的值域缩放到[0, 1]或[-1, 1]的范围内。

from sklearn.preprocessing import MinMaxScal