双曲正切函数在异常检测中的应用:识别异常数据与欺诈行为
发布时间: 2024-07-02 02:37:09 阅读量: 57 订阅数: 41 


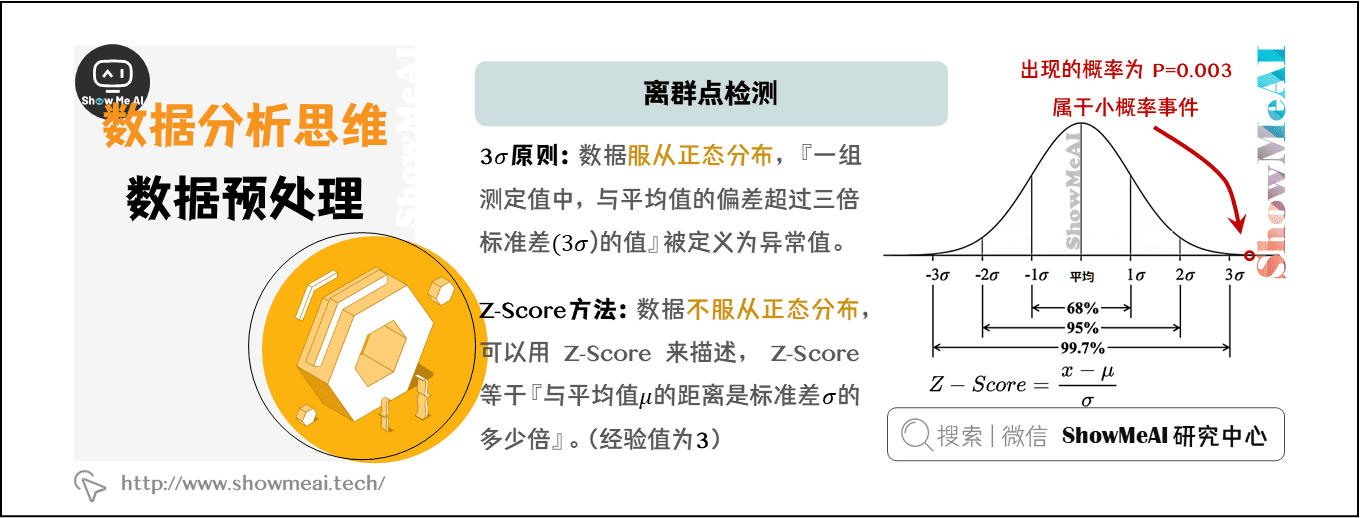
异常数据检测
# 1. 双曲正切函数的理论基础
双曲正切函数(tanh)是一种非线性函数,其数学表达式为:
```
tanh(x) = (e^x - e^(-x)) / (e^x + e^(-x))
```
该函数具有以下数学性质:
- 范围:-1 到 1
- 奇函数:tanh(-x) = -tanh(x)
- 单调递增:x > 0 时 tanh(x) > 0,x < 0 时 tanh(x) < 0
- 导数:tanh'(x) = 1 - tanh(x)^2
# 2. 双曲正切函数在异常检测中的应用
### 2.1 异常检测的基本原理
#### 2.1.1 异常数据的定义和特征
异常数据是指与正常数据明显不同的数据点,它们可能表示异常事件、错误或欺诈行为。异常数据的特征通常包括:
- **稀有性:**异常数据在数据集中出现的频率较低。
- **孤立性:**异常数据与其他数据点之间存在显著差异。
- **不可预测性:**异常数据无法通过正常数据分布模型预测。
#### 2.1.2 异常检测方法的分类
异常检测方法可分为以下几类:
- **统计方法:**基于统计分布模型,识别与模型显著不同的数据点。
- **距离方法:**计算数据点与其他数据点的距离,识别距离较大的数据点。
- **聚类方法:**将数据点聚类,识别与其他簇明显不同的数据点。
- **机器学习方法:**使用机器学习算法训练模型,识别与训练数据不同的数据点。
### 2.2 双曲正切函数的异常检测算法
#### 2.2.1 双曲正切函数的数学性质
双曲正切函数(tanh)是一种非线性函数,其取值范围为[-1, 1]。其数学表达式为:
```
tanh(x) = (e^x - e^-x) / (e^x + e^-x)
```
tanh函数具有以下性质:
- 单调递增
- 奇函数
- 对称于原点
#### 2.2.2 双曲正切函数在异常检测中的应用原理
tanh函数在异常检测中的应用原理是基于其非线性的性质。对于正常数据,tanh函数输出值接近于0,而对于异常数据,tanh函数输出值会偏离0,从而可以识别异常数据。
具体而言,异常检测算法使用tanh函数对数据进行非线性变换,然后计算变换后的数据与原数据的差值。差值较大的数据点被认为是异常数据。
```python
def tanh_anomaly_detection(data):
"""
双曲正切函数异常检测算法
参数:
data:原始数据
返回:
异常数据索引列表
"""
# 数据预处理(归一化)
data = (data - np.min(data)) / (np.max(data) - np.min(data))
# tanh变换
tanh_data = np.tanh(data)
# 计算差值
diff = np.abs(tanh_data - data)
# 识别异常数据
threshold = np.mean(diff) + 3 * np.std(diff)
anomaly_indices = np.where(diff > threshold)[0]
return anomaly_indices
```
# 3.1 数据预处理和特征工程
在异常检测的实践应用中,数据预处理和特征工程是至关重要的步骤,它们可以
0
0





