随机化算法在搜索中的应用:蒙特卡罗树搜索与遗传算法
发布时间: 2024-08-24 18:32:09 阅读量: 51 订阅数: 37 


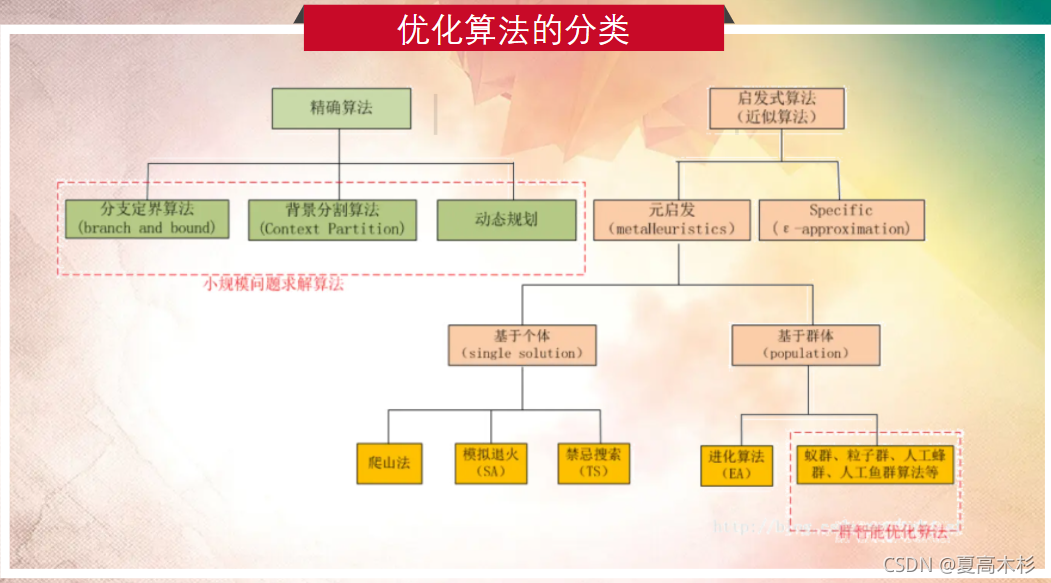
数学建模竞赛中应当掌握的十类算法
# 1. 随机化算法概述
随机化算法是一种基于概率和随机性的算法,它通过引入随机性来解决复杂问题。与传统确定性算法不同,随机化算法并不总是产生相同的输出,而是提供一个概率分布,其中每个输出都有其出现的概率。这种随机性使随机化算法能够探索更大的搜索空间,并找到传统算法可能错过的解决方案。
随机化算法通常用于解决以下类型的问题:
* **搜索和优化问题:**例如,蒙特卡罗树搜索(MCTS)和遗传算法(GA)被广泛用于搜索和优化问题。
* **规划和决策问题:**例如,MCTS被用于游戏AI和规划问题中,以做出最佳决策。
* **机器学习问题:**例如,GA被用于特征选择和优化机器学习模型。
# 2. 蒙特卡罗树搜索(MCTS)
蒙特卡罗树搜索(MCTS)是一种基于蒙特卡罗模拟和树搜索的随机化算法,广泛应用于游戏AI、规划和决策等领域。
### 2.1 MCTS的基本原理
MCTS算法的核心思想是通过模拟和搜索来探索决策树的可能路径,从而找到最优的决策。它包含两个关键步骤:
#### 2.1.1 蒙特卡罗模拟
蒙特卡罗模拟是一种随机采样技术,用于估计概率分布。在MCTS中,蒙特卡罗模拟用于生成决策树的随机路径。具体步骤如下:
- 从根节点开始,随机选择一个子节点。
- 继续选择子节点,直到到达叶节点。
- 在叶节点处,执行随机模拟,模拟游戏或决策过程的后续步骤。
- 根据模拟结果,计算叶节点的收益值。
#### 2.1.2 树搜索
树搜索是一种遍历决策树的算法,用于寻找最优路径。在MCTS中,树搜索用于选择最优的子节点。具体步骤如下:
- 从根节点开始,计算每个子节点的UCB值(置信上界)。
- 选择UCB值最高的子节点。
- 重复步骤1和2,直到到达叶节点。
### 2.2 MCTS的算法流程
MCTS算法流程主要包括以下三个阶段:
#### 2.2.1 选择阶段
在选择阶段,MCTS算法使用树搜索来选择最优的子节点。具体步骤如下:
- 从根节点开始,计算每个子节点的UCB值。
- 选择UCB值最高的子节点。
- 重复步骤1和2,直到到达叶节点。
#### 2.2.2 展开阶段
在展开阶段,MCTS算法将决策树扩展到叶节点。具体步骤如下:
- 如果叶节点没有子节点,则为其创建子节点。
- 随机选择一个子节点。
- 重复步骤1和2,直到达到预定的树深度。
#### 2.2.3 模拟阶段
在模拟阶段,MCTS算法使用蒙特卡罗模拟来评估叶节点的收益值。具体步骤如下:
- 从叶节点开始,随机选择一个子节点。
- 继续选择子节点,直到到达叶节点。
- 在叶节点处,执行随机模拟,模拟游戏或决策过程的后续步骤。
- 根据模拟结果,计算叶节点的收益值。
### 2.3 MCTS的应用场景
MCTS算法广泛应用于以下场景:
#### 2.3.1 游戏AI
MCTS算法在游戏AI中用于搜索最优的决策,例如围棋、象棋和星际争霸等游戏。
#### 2.3.2 规划和决策
MCTS算法还可用于规划和决策问题,例如路径规划、资源分配和投资决策等。
# 3.1 GA的基本原理
遗传算法(GA)是一种受自然进化过程启发的随机化算法。它模拟自然选择和遗传变异的过程,以解决优化问题。
**3.1.1 自然选择**
自然选择是进化过程的核心机制。它根据个体的适应度(生存和繁殖能力)选择个体。适应度高的个体更有可能存活和繁殖,从而将它们的基因传递给下一代。
**3.1.2 遗传变异**
遗传变异是进化过程中引入新基因的机制。它通过突变、交叉和逆转等过程发生。变异产生新的个体,这些个体可能具有不同的适应度,从而为自然选择提供原材料。
# 4. 随机化算法在搜索中的应用
### 4.1 MCTS 在搜索中的应用
#### 4.1.1 游
0
0





