神经网络控制稳定性指南：理论与应用

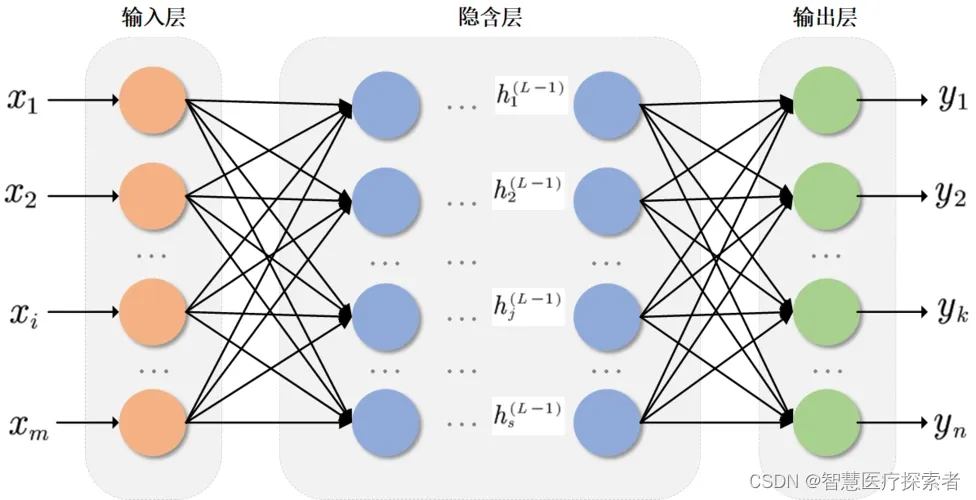
# 1. 神经网络控制基础**

神经网络控制是一种利用神经网络模型来设计和实现控制系统的技术。它通过学习和适应系统动态来提高控制性能。神经网络具有强大的非线性逼近能力，使其能够处理复杂和不确定的系统。

神经网络控制系统通常由以下几个部分组成：

- **神经网络模型：**用于学习和逼近系统动态。
- **控制器：**使用神经网络模型来生成控制信号。
- **反馈回路：**将系统输出反馈给神经网络模型，以更新其学习参数。

神经网络控制的优势包括：

- 非线性逼近能力强
- 鲁棒性好
- 自适应能力强

# 2. 神经网络控制理论

神经网络控制理论为神经网络在控制系统中的应用提供了基础。本章节将深入探讨神经网络稳定性分析和神经网络控制设计的基本原理。

### 2.1 神经网络稳定性分析

神经网络稳定性分析旨在确定神经网络系统在特定输入和初始条件下的行为。稳定性理论提供了数学工具来评估神经网络系统的稳定性。

#### 2.1.1 Lyapunov稳定性理论

Lyapunov稳定性理论是一种广泛用于分析非线性系统稳定性的方法。它基于Lyapunov函数的概念，Lyapunov函数是一个定义在系统状态空间上的标量函数，其值随着系统状态的变化而变化。

对于一个神经网络系统，如果存在一个Lyapunov函数满足以下条件，则系统是稳定的：

- **正定性：** Lyapunov函数在原点以外的值为正。
- **负定导数：** Lyapunov函数的时间导数在原点以外的值为负。

#### 2.1.2 输入到状态稳定性

输入到状态稳定性（ISS）是一种更严格的稳定性概念，它考虑了系统输入的影响。ISS系统在有界输入的情况下保持有界状态。

对于一个神经网络系统，如果存在一个ISS Lyapunov函数，则系统是ISS的。ISS Lyapunov函数满足以下条件：

- **正定性：** ISS Lyapunov函数在原点以外的值为正。
- **负定导数：** ISS Lyapunov函数的时间导数在原点以外的值为负，并且与系统输入的范数成正比。

### 2.2 神经网络控制设计

神经网络控制设计涉及利用神经网络来设计控制器，以满足特定控制目标。神经网络控制器可以实现反馈线性化、滑模控制等先进控制技术。

#### 2.2.1 反馈线性化

反馈线性化是一种控制技术，它将非线性系统转化为线性系统，从而简化控制设计。神经网络可以用于近似非线性系统中的非线性函数，从而实现反馈线性化。

#### 2.2.2 滑模控制

滑模控制是一种鲁棒控制技术，它将系统状态限制在一个称为滑模面的子流形上。神经网络可以用于设计滑模控制器，以提高系统的鲁棒性和跟踪性能。

**代码示例：**

import numpy as np
import tensorflow as tf

# 定义神经网络模型
model = tf.keras.models.Sequential([
  tf.keras.layers.Dense(10, activation='relu'),
  tf.keras.layers.Dense(1)
])

# 定义损失函数
loss_fn = tf.keras.losses.MeanSquaredError()

# 定义优化器
optimizer = tf.keras.optimizers.Adam(learning_rate=0.01)

# 训练神经网络
model.compile(optimizer=optimizer, loss=loss_fn)
model.fit(x_train, y_train, epochs=100)

# 使用训练好的神经网络进行控制
u = model.predict(x_test)

**逻