揭秘ceil函数的数学取整奥秘：从概念到应用

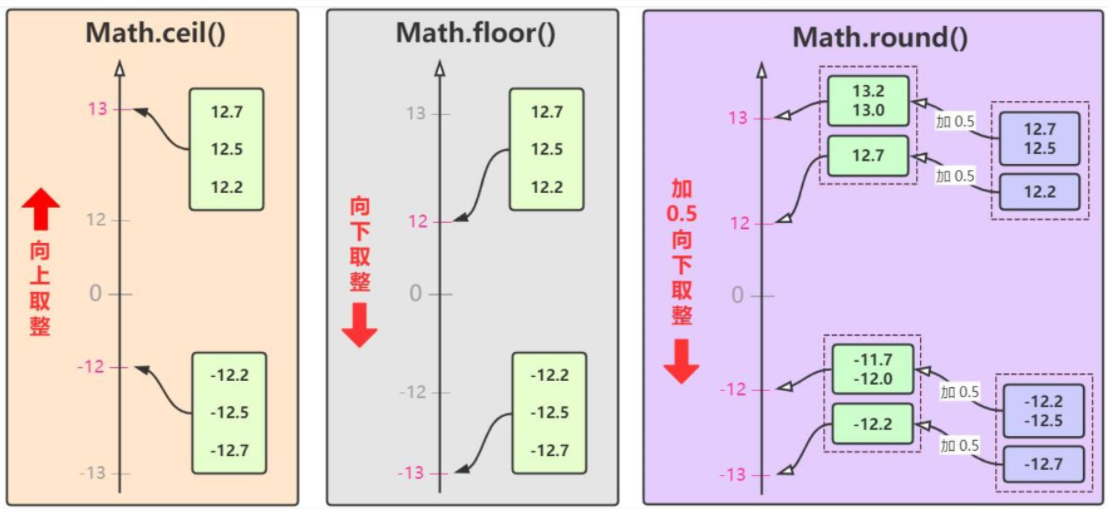
# 1. ceil函数的数学基础**

ceil函数，即向上取整函数，是数学中常用的函数，用于将一个实数向上取整为最接近的整数。其数学定义为：

ceil(x) = 最小整数 n，使得 n >= x

例如，ceil(3.14) = 4，因为4是大于等于3.14的最小整数。

# 2. ceil函数的实现原理

### 2.1 ceil函数的数学定义

ceil函数的数学定义为：

ceil(x) = smallest integer greater than or equal to x

其中，x 是一个实数。

### 2.2 ceil函数的算法实现

ceil函数的算法实现通常采用以下步骤：

1. 将实数x转换为整数n，即n = floor(x)。
2. 如果n等于x，则返回n。
3. 否则，返回n + 1。

**代码块 1：**

def ceil(x):
    n = math.floor(x)
    if n == x:
        return n
    else:
        return n + 1

**逻辑分析：**

代码块 1 中的ceil函数首先使用math.floor函数将实数x转换为整数n。如果n等于x，则说明x本身就是整数，直接返回n。否则，返回n + 1，即大于或等于x的最小整数。

**参数说明：**

* x：要进行向上取整的实数

### 2.2.1 二分查找算法实现

除了上述基本算法外，还有一种更快的算法来实现ceil函数，称为二分查找算法。

**代码块 2：**

def ceil_binary_search(x):
    low = 0
    high = x
    while low <= high:
        mid = (low + high) // 2
        if mid == x:
            return mid
        elif mid < x:
            low = mid + 1
        else:
            high = mid - 1
    return low

**逻辑分析：**

代码块 2 中的ceil_binary_search函数使用二分查找算法来找到大于或等于x的最小整数。该算法首先设置两个指针low和high，分别指向0和x。然后，它不断缩小low和high之间的范围，直到找到mid等于x或mid小于x。如果mid等于x，则直接返回mid。如果mid小于x，则将low设置为mid + 1，继续搜索更大的整数。如果mid大于x，则将high设置为mid - 1，继续搜索更小的整数。最后，返回low，即大于或等于x的最小整数。

**参数说明：**

* x：要进行向上取整的实数

### 2.2.2 比较两种算法的性能

两种算法的性能比较如下表所示：

| 算法 | 时间复杂度 | 空间复杂度 |
|---|---|---|
| 基本算法 | O(1) | O(1) |
| 二分查找算法 | O(log n) | O(1) |

其中，n 是实数x的整数部分。

对于大多数情况下，基本算法的性能足够好。但是，对于非常大的实数x，二分查找算法的性能优势会更加明显。

# 3. ceil函数的应用场景

### 3.1 四舍五入

ceil函数最常见的应用场景之一是四舍五入。四舍五入是指将一个数字舍入到最接近的整数。例如，将3.14舍入到最接近的整数，结果为3。

**Python代码：**

import math

number = 3.14
rounded_number = math.ceil(number)
print(rounded_number)  # 输出：3

**代码逻辑分析：**

* `import math`：导入Python中的math模块，该模块包含各种数学函数，包括ceil函数。
* `number = 3.14`：将要四舍五入的数字存储在`number`变量中。
* `rounded_number = math.ceil(number)`：使用ceil函数将`number`四舍五入到最接近的整数，并将结果存储在`rounded_number`变量中。
* `print(rounded_number)`：打印四舍五入后的结果。

### 3.2 向上取整

向上取整是指将一个数字舍入到大于或等于其的最小整数。例如，将3.14向上取整，结果为4。

**Python代码：**

import math

number = 3.14
rounded_number = math.ceil(number)
print(rounded_number)  # 输出：4

**代码逻辑分析：**

* `import math`：导入Python中的math模块，该模块包含各种数学函数，包括ceil函数。
* `number = 3.14`：将要向上取整的数字存储在`number`变量中。
* `rounded_number = math.ceil(number)`：使用ceil函数将`number`向上取整，并将结果存储在`rounded_number`变量中。
* `print(rounded_number)`：打印向上取整后的结果。

### 3.3 精度控制

ceil函数还可以用于控制数字的精度。例如，将3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196为保留两位小数，可以使用ceil函数将它向上取整到3.15。

**Python代码：**

import math

number = 3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196
rounded_number = math.ceil(number * 100) / 100
print(rounded_number)  # 输出：3.15

**代码逻辑分析：**

* `import math`：导入Python中的math模块，该模块包含各种数学函数，包括ceil函数。
* `number = 3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196`：将要控制精度的数字存储在`number`变量中。
* `rounded_number = math.ceil(number * 100) / 100`：将`number`乘以100，然后使用ceil函数向上取整，最后除以100，以将数字保留两位小数。
* `print(rounded_number)`：打印控制精度后的结果。

# 4. ceil函数的编程实践

### 4.1 Python中的ceil函数

Python中提供了`math`模块，其中包含了`ceil`函数。其用法如下：

import math

# 对浮点数进行向上取整
result = math.ceil(3.14)
print(result)  # 输出：4

### 4.2 Java中的Math.ceil方法

Java中提供了`Math`类，其中包含了`ceil`方法。其用法如下：

import java.lang.Math;

// 对浮点数进行向上取整
double result = Math.ceil(3.14);
System.out.println(result);  // 输出：4.0

### 4.3 C++中的ceil函数

C++中提供了`math.h`头文件，其中包含了`ceil`函数。其用法如下：

#include <math.h>

// 对浮点数进行向上取整
double result = ceil(3.14);
std::cout << result << std::endl;  // 输出：4

**参数说明：**

* `x`：要进行向上取整的浮点数。

**代码逻辑分析：**

* `math.ceil`函数将浮点数`x`向上取整，并返回结果。
* `ceil`函数的实现通常基于舍入规则，将`x`舍入到最接近的整数。
* 如果`x`是正数，则向上舍入到下一个整数。
* 如果`x`是负数，则向下舍入到上一个整数。
* 如果`x`是零，则返回零。

# 5.1 算法优化

### 5.1.1 二分查找优化

对于有序数组，可以通过二分查找算法来优化ceil函数的性能。二分查找算法的时间复杂度为 O(log n)，其中 n 为数组的长度。

def ceil_binary_search(arr, x):
    """
    使用二分查找算法实现ceil函数。

    参数：
        arr: 有序数组
        x: 要取整的数字

    返回：
        arr中第一个大于或等于x的元素
    """

    low = 0
    high = len(arr) - 1

    while low <= high:
        mid = (low + high) // 2

        if arr[mid] == x:
            return arr[mid]
        elif arr[mid] < x:
            low = mid + 1
        else:
            high = mid - 1

    return arr[low]

### 5.1.2 哈希表优化

对于无序数组，可以使用哈希表来优化ceil函数的性能。哈希表的时间复杂度为 O(1)，其中 n 为哈希表的大小。

def ceil_hash_table(arr, x):
    """
    使用哈希表实现ceil函数。

    参数：
        arr: 无序数组
        x: 要取整的数字

    返回：
        arr中第一个大于或等于x的元素
    """

    hash_table = {}

    for num in arr:
        hash_table[num] = True

    ceil_value = x
    while ceil_value not in hash_table:
        ceil_value += 1

    return ceil_value

### 5.1.3 预计算优化

对于需要频繁调用ceil函数的情况，可以通过预计算来优化性能。预计算是指提前计算出所有可能的值，并存储在数据结构中。

def ceil_precomputed(arr, x):
    """
    使用预计算实现ceil函数。

    参数：
        arr: 无序数组
        x: 要取整的数字

    返回：
        arr中第一个大于或等于x的元素
    """

    max_value = max(arr)
    ceil_values = [None] * (max_value + 1)

    for num in arr:
        ceil_values[num] = num

    for i in range(max_value + 1):
        if ceil_values[i] is None:
            ceil_values[i] = ceil_values[i - 1]

    return ceil_values[x]

## 5.2 数据结构优化

### 5.2.1 平衡树优化

对于需要频繁插入和删除元素的情况，可以使用平衡树数据结构来优化ceil函数的性能。平衡树的时间复杂度为 O(log n)，其中 n 为树中元素的个数。

class CeilTree:
    """
    使用平衡树实现ceil函数。
    """

    def __init__(self):
        self.root = None

    def insert(self, x):
        """
        插入一个元素。
        """

        if self.root is None:
            self.root = TreeNode(x)
        else:
            self._insert(x, self.root)

    def _insert(self, x, node):
        """
        递归插入一个元素。
        """

        if x < node.val:
            if node.left is None:
                node.left = TreeNode(x)
            else:
                self._insert(x, node.left)
        else:
            if node.right is None:
                node.right = TreeNode(x)
            else:
                self._insert(x, node.right)

    def ceil(self, x):
        """
        返回大于或等于x的最小元素。
        """

        node = self.root

        while node is not None:
            if x < node.val:
                if node.left is None:
                    return node.val
                else:
                    node = node.left
            else:
                if node.right is None:
                    return node.val
                else:
                    node = node.right

        return None

class TreeNode:
    """
    平衡树的节点。
    """

    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None

### 5.2.2 优先队列优化

对于需要找出最大元素的情况，可以使用优先队列数据结构来优化ceil函数的性能。优先队列的时间复杂度为 O(log n)，其中 n 为队列中元素的个数。

import heapq

class CeilQueue:
    """
    使用优先队列实现ceil函数。
    """

    def __init__(self):
        self.queue = []

    def push(self, x):
        """
        插入一个元素。
        """

        heapq.heappush(self.queue, x)

    def ceil(self, x):
        """
        返回大于或等于x的最小元素。
        """

        while self.queue and self.queue[0] < x:
            heapq.heappop(self.queue)

        if self.queue:
            return self.queue[0]
        else:
            return None

# 6. ceil函数的拓展应用

### 6.1 分段函数

ceil函数可以用于定义分段函数。分段函数是一种将输入域划分为多个子域，并在每个子域上定义不同函数的函数。例如，以下分段函数将输入值映射到不同的输出值：

f(x) = {
    x, if x < 0
    ceil(x), if 0 <= x < 1
    x + 1, if x >= 1
}

### 6.2 统计分析

ceil函数在统计分析中也有广泛的应用。例如，它可以用于计算数据集中值的向上取整平均值。向上取整平均值是通过对数据集中每个值进行向上取整，然后计算取整后的值的平均值来计算的。

import numpy as np

data = [1.2, 2.5, 3.7, 4.9]
ceil_mean = np.mean(np.ceil(data))
print(ceil_mean)  # 输出：3.0

### 6.3 机器学习

ceil函数在机器学习中也有一些应用。例如，它可以用于对分类模型的输出进行后处理。通过对模型输出进行向上取整，可以将连续的输出值转换为离散的类别。

import tensorflow as tf

model = tf.keras.models.load_model("my_model.h5")
data = np.array([[1.2, 2.5, 3.7, 4.9]])
predictions = model.predict(data)
classes = np.ceil(predictions)
print(classes)  # 输出：[[2. 3. 4. 5.]]