【递归算法可视化指南】：直观理解递归结构与流程的艺术

# 1. 递归算法的基本概念与重要性

## 1.1 递归算法简介
递归算法是一种在解决问题时反复调用自身函数的方法。这种技术在解决可以分解为相似子问题的问题时尤其有用，如树的遍历和排序算法。递归算法的代码通常很简洁，但需仔细设计以避免性能问题。

## 1.2 递归与复杂问题解决
在编程中，递归提供了一种优雅的方式来处理具有自然层次结构的问题。例如，在解析文件系统、遍历文件目录结构或生成组合和排列时，递归算法可以显著简化代码。

## 1.3 递归的重要性
递归的灵活性和简洁性使其成为理解和学习算法与数据结构不可或缺的部分。它教会我们如何将大问题分解为更小的部分，并教会我们如何用递归思想来思考和解决问题。尽管递归有其局限性，如栈溢出风险和性能问题，但通过理解和练习递归，我们可以发展出强大的问题解决技能。

# 2. 递归算法的理论基础

## 2.1 递归的定义与原理

### 2.1.1 递归的数学定义

递归在数学中的定义是一种通过定义自身来解决问题的函数。直观上说，递归函数会调用自身来解决问题的子部分，直到达到某个基本情况（base case），从而能够给出解决方案。递归的核心在于将一个复杂的问题分解成一个或多个相似但更简单的子问题。

一个递归定义通常包含两部分：基本情况和递归步骤。基本情况是递归函数不进行进一步递归调用，直接返回结果的情形。递归步骤则描述了如何利用更小的子问题的解来构建原问题的解。

### 2.1.2 递归的工作原理

从工作原理上看，递归函数在每次调用自身时，实际上是在创建一个新的函数调用栈（call stack）。这个栈中会保存函数调用的状态，包括局部变量和返回地址。当遇到基本情况时，递归函数会逐步返回，每一次返回都意味着解出了一个子问题，并利用这些子问题的解来构建更大问题的解。

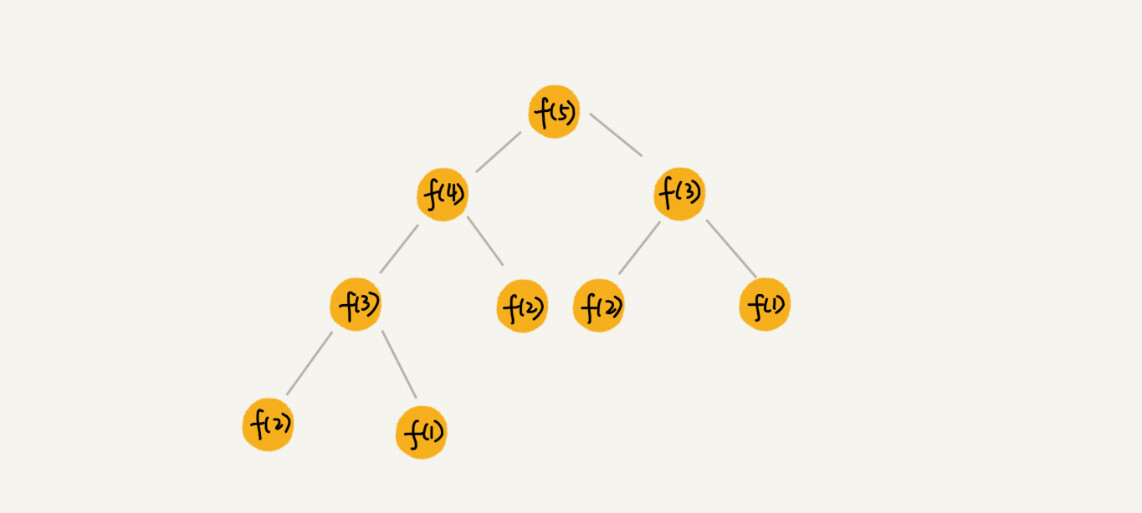
例如，在斐波那契数列的计算中，我们定义`F(0)=0`和`F(1)=1`为基本情况，而`F(n)=F(n-1)+F(n-2)`为递归步骤。在实际计算`F(n)`时，函数会不断地调用自身来计算`F(n-1)`和`F(n-2)`，直至遇到基本情况。

## 2.2 递归函数的设计要素

### 2.2.1 基本情况与递归情况的识别

在设计递归函数时，确定基本情况至关重要。基本情况是递归终止的地方，它决定了递归何时停止，否则会导致无限递归，最终导致栈溢出错误。递归情况则是函数如何将原问题分解成更小问题的地方。

识别基本情况需要分析问题并确定递归能够达到的终点条件。通常，这些条件是问题规模缩小到最简单或已知答案的情形。递归情况则要确保每次递归调用都在向基本情况靠近，否则递归将无法收敛到解。

### 2.2.2 递归深度与性能问题

递归深度是递归函数在一次执行中达到的最大调用深度。递归深度直接关联到栈空间的使用量，过深的递归可能导致栈溢出。因此，在设计递归函数时，需要考虑递归深度和栈的限制。

性能问题主要体现在递归调用的开销和重复计算上。每次递归调用都会带来额外的开销，例如函数调用的参数传递和返回地址的保存。此外，没有妥善设计的递归可能导致对相同子问题的重复求解，这可以通过记忆化（memoization）技术来优化，缓存已经计算过的子问题解以避免重复计算。

## 2.3 递归算法的类型与适用场景

### 2.3.1 直接递归与间接递归

直接递归指的是函数直接调用自身。例如，计算斐波那契数列的函数就是直接递归的典型例子。间接递归则涉及多个函数之间的相互调用，例如函数A调用函数B，函数B又调用函数A。间接递归需要更加谨慎地设计，以防止无限循环。

### 2.3.2 递归与迭代的比较

递归和迭代是编程中解决重复问题的两种不同方法。迭代通常使用循环结构来重复执行代码块，而递归则通过函数调用自身来重复执行。递归代码通常更简洁，易于理解和实现，但可能在性能上不如迭代。迭代在处理有明确循环边界和迭代状态管理的问题时往往更加高效。

### 2.3.3 典型递归算法案例分析

一个典型的递归算法案例是快速排序算法。快速排序在排序一个数组时，会选取一个基准元素（pivot），然后将数组分为两部分，一部分包含所有小于基准的元素，另一部分包含所有大于基准的元素。随后递归地对这两部分进行排序。在快速排序的每个递归调用中，都会减少数组的规模，直至达到基本情况，即数组为空或只有一个元素。

接下来，我们将深入探讨递归算法的可视化工具与方法，以及如何在实际编程中应用这些理论基础。

# 3. 递归算法的可视化工具与方法

## 3.1 可视化工具的选择与使用

在深入理解递归算法之后，可视化工具成为理解复杂递归过程和结构的有力辅助。它们能够将抽象的代码逻辑转换为直观的图形表示，帮助开发者更好地分析和调试递归算法。

### 3.1.1 选择合适的可视化工具

选择一个合适的可视化工具需要考虑多个因素，包括支持的编程语言、图表类型、可定制性以及社区支持等。例如，对于通用的递归流程可视化，可以考虑使用Mermaid，它是一个基于文本的图表定义语言，可以通过简单的文本描述创建流程图、序列图、甘特图等多种类型的图表。

对于更专业的场景，如需要动态展示数据结构的递归调用过程，可以选择像VSDC Free Video Editor这样的视频制作工具，它支持逐帧编辑，可以用来制作递归算法的动画演示。

### 3.1.2 工具的安装与初步配置

以Mermaid为例，它可以通过npm安装为Node.js的包，也可以使用一些在线编辑器来直接运行Mermaid代码。以下是一个简单的示例流程图的Mermaid代码：

graph TD;
    A[开始] --> B{判断基本条件};
    B -- 是 --> C[递归结束];
    B -- 否 --> D[递归调用];
    D --> B;

将上述代码粘贴到支持Mermaid的编辑器中，即可生成对应的流程图。这个流程图简单地展示了递归算法的基本结构：判断基本条件、结束或继续递归调用。

## 3.2 递归流程的可视化技巧

可视化不仅仅是将代码转化为图表，更是通过这些图表帮助开发者理解算法的工作原理。

### 3.2.1 概念图与流程图的绘制

概念图帮助开发者理解递归算法中的函数调用关系，流程图则帮助理解算法的逻辑流程。使用像Lucidchart或draw.io这样的工具，可以手绘或通过模板快速生成流程图