【组合问题终极解法】：递归与回溯的完美融合

# 1. 递归与回溯的概念解析

递归与回溯是算法设计中两个密切相关的概念，它们在解决复杂问题时经常被应用到。递归是通过函数自己调用自己来解决问题的方法，它将大问题分解成小问题，直至达到一个基本情况。而回溯是一种系统地搜索问题的解决方案的方法，它尝试分步的去解决一个问题，在分步解决问题的过程中，当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候，它将取消上一步甚至是上几步的计算，再通过其他的可能的分步解答再次尝试寻找问题的答案。

递归与回溯的关系非常紧密，递归是实现回溯的基础，回溯是递归问题解决的一种方法。在实际应用中，递归常常是实现回溯的首选方式，因为它可以自然地模拟出回溯的过程，使得算法的实现更为简洁明了。

理解这两者的概念对掌握其深层次的算法应用至关重要，因为它们不仅仅是编程技巧，更是解决复杂问题的策略和思维模式。接下来的章节，我们将深入探讨递归与回溯算法的理论基础、实践应用，以及它们在实际问题解决中的高级技巧。

# 2. 递归算法的理论基础与实践

## 2.1 递归算法的核心原理

### 2.1.1 递归函数的定义与构成

递归函数是递归算法的核心组件，其定义本质上是一个自身调用自身的函数。在计算机科学中，递归函数通过不断地调用自身来解决更小的子问题，最终解决原始问题。

def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n - 1)

在上面的代码中，`factorial` 函数是一个递归函数，用来计算阶乘。它的构成包含两个主要部分：基本情况（或称终止条件），即 `if n == 0` 时，返回 1；以及递归步骤，即 `else` 分支中的 `n * factorial(n - 1)`，它将问题规模缩小，并递归调用函数自身。

### 2.1.2 递归调用的执行过程

递归调用的执行过程涉及到函数调用栈的使用。每次函数调用都会在栈上增加一个新的栈帧，其中包含了函数的局部变量、参数、返回地址等信息。

以计算 5 的阶乘为例，我们可以可视化递归调用的过程：

graph TD
    A[Start] --> B[5 * factorial(4)]
    B --> C[4 * factorial(3)]
    C --> D[3 * factorial(2)]
    D --> E[2 * factorial(1)]
    E --> F[1 * factorial(0)]
    F --> G[Return 1]
    G --> H[Return 2]
    H --> I[Return 6]
    I --> J[Return 24]
    J --> K[Return 120]

当 `n == 0` 时，函数返回 1，不再递归调用，然后逐层返回，完成整个计算过程。

## 2.2 递归算法的设计技巧

### 2.2.1 如何寻找递归关系式

递归关系式是将大问题分解为小问题的数学表达形式。寻找递归关系式通常遵循以下步骤：

1. **确定问题的规模**：明确原问题与子问题的规模关系。
2. **分析关系规律**：找出原问题与子问题之间的递推规律。
3. **建立递归式**：根据找到的规律，编写递归函数的框架。

例如，在计算斐波那契数列时，递归关系式为 `F(n) = F(n-1) + F(n-2)`。

### 2.2.2 递归终止条件的确定

递归终止条件是递归函数的关键。没有正确的终止条件，递归将无限进行下去，最终可能导致栈溢出错误。终止条件通常根据问题的自然边界确定。例如，阶乘函数的终止条件是 `n == 0`。

def fibonacci(n):
    if n <= 1:  # 终止条件
        return n
    else:
        return fibonacci(n-1) + fibonacci(n-2)

### 2.2.3 递归解法与迭代解法的比较

递归解法和迭代解法都可以解决相同的问题，但它们在思想和性能上有显著差异。递归解法代码简洁，逻辑直观，但可能因递归调用栈过深导致栈溢出，且性能可能低于迭代解法。迭代解法通常使用循环结构，消耗较少的内存，但可能代码更加复杂。

# 递归版本的 Fibonacci 函数
def fibonacci(n):
    if n <= 1:
        return n
    return fibonacci(n-1) + fibonacci(n-2)

# 迭代版本的 Fibonacci 函数
def fibonacci_iterative(n):
    a, b = 0, 1
    for _ in range(n):
        a, b = b, a + b
    return a

在递归版本中，我们反复调用 `fibonacci` 函数自身，而在迭代版本中，我们使用循环和简单的变量更新来解决问题。

## 2.3 递归算法的优化策略

### 2.3.1 记忆化递归与空间复杂度优化

记忆化递归通过使用缓存来存储已解决子问题的结果，避免重复计算，从而减少不必要的计算量。空间复杂度优化涉及到减少额外的空间开销，比如使用尾递归。

# 记忆化递归实现 Fibonacci 数列
def fibonacci_memo(n, memo={}):
    if n in memo:
        return memo[n]
    if n <= 1:
        return n
    memo[n] = fibonacci_memo(n-1, memo) + fibonacci_memo(n-2, memo)
    return memo[n]

在上述代码中，`memo` 字典用于存储已经计算过的阶数值，以避免重复计算。

### 2.3.2 尾递归优化与编译器优化

尾递归是一种特殊的递归形式，其中递归调用是函数体中的最后一个操作。对于支持尾调用优化的编译器或解释器，尾递归可以被优化为迭代过程，从而避免增加额外的栈帧，减少空间复杂度。

def factorial_tail(n, accumulator=1):
    if n == 0:
        return accumulator
    return factorial_tail(n - 1, accumulator * n)

在上面的代码中，`accumulator` 参数用于累积结果，这样的设计允许函数以尾递归形式编写。

以上内容只是第2章节中递归算法基础与实践的部分内容。每一节的深度内容确保了理解递归算法的核心原理、设计技巧和优化策略。第3章将进一步探讨回溯算法，最终第5章将深入讨论递归与回溯算法的应用和未来趋势。

# 3. 回溯算法的理论基础与实践

## 3.1 回溯算法的基本框架
### 3.1.1 回溯法的定义与特点
回溯算法（Backtracking Algorithm）是一种通过递归来搜索问题解空间的算法。它利用试错的思想，通过逐步构建候选解并判断候选解是否符合问题的约束条件，来探索所有可能的解空间路径。当发现当前候选解不可能达到满意的结果时，算法会通过回溯的方式放弃当前路径，即撤销上一步或者上几步的操作，再尝试其他可能的解空间路径。

回溯算法的特点是能够系统地搜索潜在的解空间，并且能够有效地剪枝，避免不必要的计算。它常用于解决组合问题，如八皇后问题、图的着色、旅行商问题等。

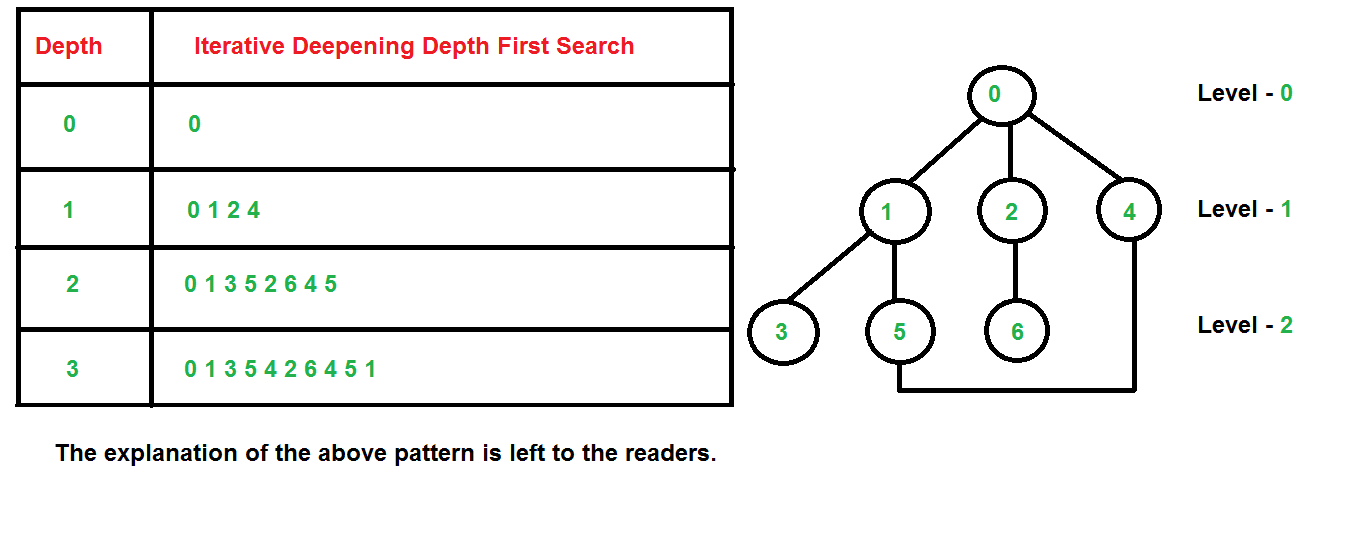
### 3.1.2 回溯搜索树的构建与遍历
构建回溯搜索树是回溯算法中关键的步骤。搜索树的每个节点表示问题的一个状态，节点的子节点表示状态的拓展。在这棵树中，一个可行解通常对应一条从根节点到叶子节点的路径。

回溯搜索树的遍历方式遵循深度优先搜索的原则，即尽可能深地搜索树的分支。当节点v的所有子节点都已被探寻过后，搜索将回溯到发现节点v的那条路径上的上一个节点。这个过程一直进行到找到所需的解或已访问完所有节点为止。

为了高效地实现回溯搜索，我们通常使用递归函数来表示这种遍历过程。以下是一个构建回溯搜索树的伪代码示例：

void backtrack(node v) {
    if (v is a solution) {
        process(v)
    }
    else {
        for (each child u of v) {
            if (isValid(u)) {
                makeMove(u) // 在此增加u节点