【递归与迭代的终极对决】：如何在实际问题中做出最佳选择

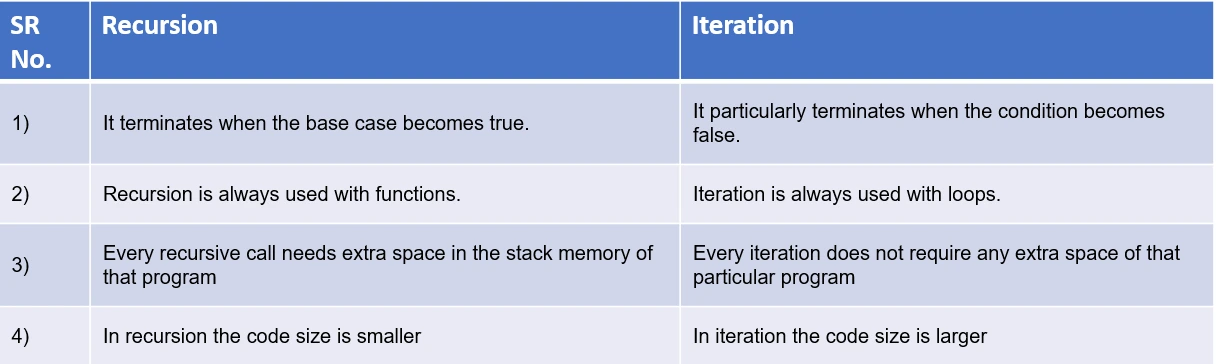
# 1. 递归与迭代概念解析

## 1.1 递归与迭代的基础理解
递归和迭代是编程中常见的两种解决问题的方法。递归是函数直接或间接调用自身来解决问题的过程，形象地可比作“分而治之”。而迭代则是通过重复执行一系列操作来逐渐逼近结果的方法，类似于“逐一击破”。

## 1.2 递归的原理与特点
递归算法的设计依赖于将问题分解成更小的子问题，直至达到一个可直接解决的基准条件。递归的典型特点是简洁、直观，但可能会因为重复调用导致较大的空间开销。

## 1.3 迭代的原理与特点
迭代算法通过循环结构在有限步骤内重复利用一系列指令完成任务，其核心在于用状态的变更来推动计算过程。迭代的优点是节省空间，但有时编写起来比递归复杂。

在接下来的章节中，我们将深入探讨递归和迭代在算法设计中的应用，以及它们在性能和优化方面各自的优势和局限。

# 2. 递归与迭代在算法中的应用

### 2.1 理解递归算法设计

#### 2.1.1 递归的基本原理

递归是计算机科学中的一种重要技术，它允许一个函数直接或间接地调用自身。基本原理是将大问题分解为小问题，直到这些小问题变得足够简单以至于可以直接解决。递归算法的关键在于找到能够将问题规模缩小的递归表达式，并确定递归的终止条件。

递归的两个核心要素是边界条件和递归体。边界条件定义了递归何时停止，通常为问题规模缩小到最简单形态时，而递归体则是算法的主体，描述了如何通过递归解决小规模问题进而解决原问题。

def factorial(n):
    # 边界条件：若n为0，则返回1
    if n == 0:
        return 1
    # 递归体：n的阶乘等于n乘以(n-1)的阶乘
    else:
        return n * factorial(n - 1)

在上述阶乘函数`factorial`中，如果`n`是0，函数返回1（边界条件）。否则，它会返回`n`乘以`factorial(n - 1)`的结果（递归体）。每次递归调用都会将`n`减小1，直到达到边界条件。

#### 2.1.2 递归算法的结构和模式

递归算法通常遵循一种固定的结构模式，它包括初始化和递归过程。初始化通常涉及设置初始参数和检查基本情况以直接得出结果。递归过程涉及函数调用自身来处理规模缩小后的问题。

def recursive_sum(arr, n):
    # 边界条件
    if n <= 0:
        return 0
    else:
        # 递归体
        return arr[n-1] + recursive_sum(arr, n-1)

# 初始化调用
arr = [1, 2, 3, 4, 5]
print(recursive_sum(arr, len(arr)))

在`recursive_sum`函数中，我们定义了如何对数组`arr`中的元素求和。如果数组大小`n`不大于0（基本情况），我们返回0。否则，我们将数组的最后一个元素与递归调用函数自身计算的前`n-1`个元素的和相加。

递归算法的模式也可以用下面的伪代码表示：

Function RecursiveAlgorithm(parameters)
    if BaseCondition(parameters) then
        return BaseCaseResult
    else
        result = RecursiveAlgorithm(adjustedParameters)
        return ComputedResultBasedOnResult
    end if
end Function

这种模式的关键在于调整参数以缩小问题规模，并计算基于递归结果的结果。

### 2.2 理解迭代算法设计

#### 2.2.1 迭代的基本原理

迭代算法使用循环结构（如for、while循环）逐步重复执行算法的计算和操作，直到满足某个条件时停止。基本原理是重复执行一组指令，直到某个控制条件不再满足为止。迭代算法通常更容易理解和实现，因为它们不需要理解复杂的调用栈和递归堆栈。

迭代算法的设计依赖于确定迭代次数和每次迭代时如何更新状态。下面是一个迭代求和的例子：

def iterative_sum(arr):
    total = 0
    for num in arr:
        total += num
    return total

# 调用
arr = [1, 2, 3, 4, 5]
print(iterative_sum(arr))

迭代求和函数`iterative_sum`通过一个循环累加数组`arr`中的每个元素。循环逐步增加`total`的值，直到所有元素都被处理。

#### 2.2.2 迭代算法的结构和模式

迭代算法的结构相对简单，通常包括初始化、迭代条件以及迭代体。初始化步骤准备算法运行需要的变量。迭代条件是必须满足的条件，以便算法可以继续执行。迭代体是算法的核心部分，描述了如何更新状态和进行下一步迭代。

def fib_iterative(n):
    a, b = 0, 1
    for _ in range(n):
        a, b = b, a + b
    return a

# 调用
print(fib_iterative(10))

在这个迭代计算斐波那契数列的例子中，`a`和`b`两个变量分别初始化为序列的前两个数。在每次迭代中，变量的值被更新为序列的下一个值。迭代继续，直到计算出所需的斐波那契数。

迭代算法的模式也可以用以下伪代码表示：

Initialize variables
while Condition is true do
    Update variables
end while
return FinalResult

迭代算法的每一步都是明确的，通过逐步更新变量最终得到结果。

### 2.3 递归与迭代的性能比较

#### 2.3.1 时间复杂度分析

在性能分析中，时间复杂度用来量化算法运行时间与输入大小之间的关系。递归和迭代算法在时间复杂度上的差异主要取决于它们解决问题的方式和额外开销。

递归算法可能会因为重复计算相同的子问题而效率低下，尤其是在没有采用优化措施（如记忆化递归）的情况下。每次递归调用都可能带来额外的开销，如函数调用栈和上下文切换的开销。

# 递归计算斐波那契数列的时间复杂度分析
def recursive_fib(n):
    if n <= 1:
        return n
    else:
        return recursive_fib(n - 1) + recursive_fib(n - 2)

# 时间复杂度为O(2^n)，非常低效

在上面的例子中，递归计算斐波那契数的时间复杂度是指数级的`O(2^n)`，因为每个递归调用都会产生两个递归调用，直到达到基本情况。

与此相反，迭代算法的时间复杂度通常更可预测，因为它避免了递归的额外开销。对于同一个问题，迭代算法往往可以实现更低的时间复杂度。

# 迭代计算斐波那契数列的时间复杂度分析
def iterative_fib(n):
    a, b = 0, 1
    for _ in range(n):
        a, b = b, a + b
    return a

# 时间复杂度为O(n)，更高效

在迭代版本中，时间复杂度是线性的`O(n)`，因为算法只需要遍历`n`次来计算结果。

#### 2.3.2 空间复杂度分析

空间复杂度度量了算法在执行期间临时占用存储空间的大小。递归算法的空间复杂度往往比迭代算法高，因为它需要为每一次递归调用分配新的栈空间。

# 递归计算斐波那契数列的空间复杂度分析
def recursive_fib(n):
    if n <= 1:
        return n
    else:
        return recursive_fib(n - 1) + recursive_fib(n - 2)

# 空间复杂度为O(n)，因为需要存储调用栈

在递归版本中，每次函数调用都需要存储在调用栈上，因此空间复杂度与递归深度相关，对于斐波那契数列是`O(n)`。

迭代算法通常使用固定数量的变量和数据结构，因此空间复杂度较低。在某些情况下，迭代算法甚至可以在常数空间内完成，即`O(1)`的空间复杂度。

# 迭代计算斐波那契数列的空间复杂度分析
def iterative_fib(n):
    a, b = 0, 1
    for _ in range(n):
        a, b = b, a + b
    return a

# 空间复杂度为O(1)，因为只需要固定大小的变量

在迭代版本中，算法的空间复杂度为常数`O(1)`，因为只需要固定数量的变量来完成计算，不需要额外的栈空间。

在比较递归和迭代时，通常需要权衡算法的时间和空间复杂度，以及它们在特定场景下的实际表现。在某些情况下，递归算法由于其代码简洁和易于理解的特性而更受青睐；而在其他情况下，迭代算法则因其较低的空间开销和可能的性能优势而更受欢迎。

# 3. 递归与迭代在实际问题中的抉择

在算法设计和实现中，递归与迭代的选择一直是技术人员面临的难题之一。每种方法都有其优势和局限性，因此，在不同的应用场景下，如何做出最优选择至关重要。本章将深入探讨递归与迭代在实际问题中的抉择，并通过场景分析、案例研究来阐述它们的应用和优缺点。

## 3.1 选择递归的场景分析

递归方法在某些特定问题上具有独到的优势，尤其是那些能够自然地分解