【递归错误处理指南】：异常情况下的递归回溯与恢复策略

# 1. 递归错误处理的基本概念

在编程领域，递归是一种常见的算法设计技巧，用于解决可以分解为多个相似子问题的问题。虽然递归提供了简洁和直观的解决方案，但同时也引入了错误处理的复杂性。递归错误处理涉及理解和诊断在递归执行过程中出现的问题，以确保程序能够稳定运行并正确响应异常情况。

## 递归的基本原理

递归函数调用自身以解决问题的子集，直到达到基本情况（base case），然后逐级返回结果。递归的每一步都依赖于前一步的正确执行，因此错误处理成为递归设计中不可或缺的一部分。

## 错误处理的重要性

由于递归函数的每一层都会消耗系统资源（如内存和处理器时间），错误处理不仅可以避免资源浪费，还可以防止整个程序因未处理的异常而崩溃。有效的错误处理机制能够确保递归算法的健壮性和可靠性。

# 2. 递归函数的错误类型与诊断

### 2.1 递归函数的常见错误类型

#### 2.1.1 栈溢出与深度限制

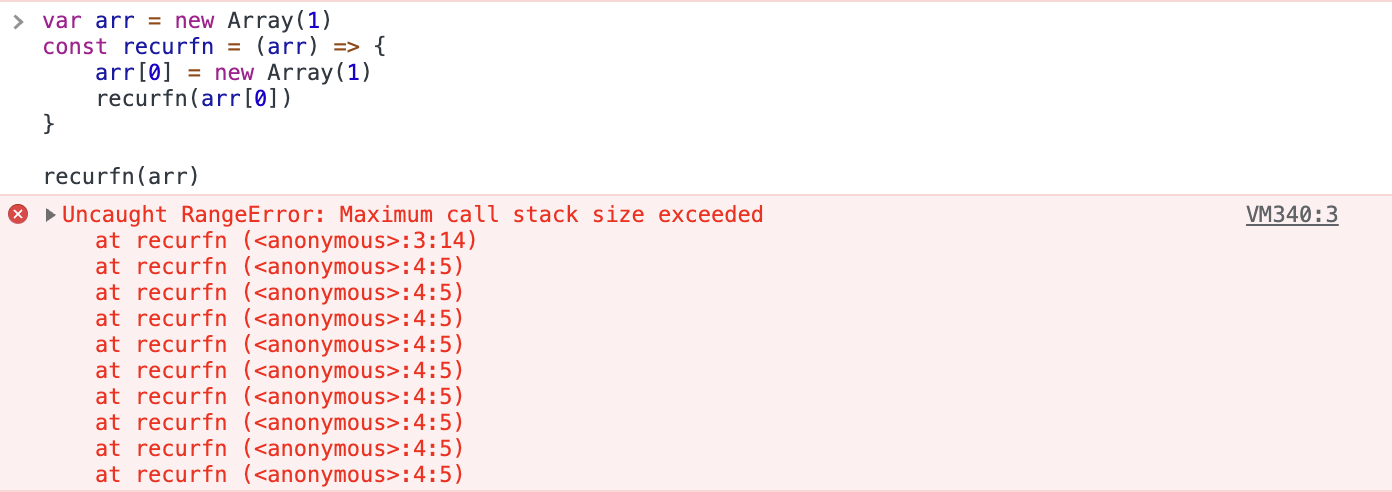
递归函数的错误类型中，栈溢出是一个常见且严重的错误，尤其是在深度递归的场景中。在递归过程中，每一次递归调用都会在调用栈上增加一层，如果递归深度太大，超过了系统分配给程序的栈空间，就会发生栈溢出错误。

现代编程语言通常会有一个递归深度的限制，例如Python默认的递归深度限制是1000。当递归函数的深度超过了这个限制时，系统会抛出`RecursionError`异常。

代码示例：

def recursive_function(level):
    if level > 1000:
        raise RecursionError("Recursion depth exceeded")
    return recursive_function(level + 1)

try:
    recursive_function(1)
except RecursionError as e:
    print(e)

逻辑分析与参数说明：
在上面的Python示例中，`recursive_function`函数会无限递归下去，直到达到1000层深度时抛出异常。`RecursionError`异常是Python中处理栈溢出的标准方式，可以捕获并处理这类错误，避免程序崩溃。

#### 2.1.2 参数传递错误与边界条件失控

递归函数依赖于参数的正确传递，错误的参数值可能导致递归调用行为不符合预期，甚至导致无限递归。边界条件的不正确处理是递归错误的另一个主要原因。

代码示例：

def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n)  # 错误的递归调用

print(factorial(5))  # 将导致无限递归

逻辑分析与参数说明：
在上述代码中，计算阶乘的递归函数`factorial`有一个明显的错误，在递归调用中错误地传入了`n`而不是`n-1`。这将导致每次递归调用都重复使用相同的参数`n`，而不是逐步接近终止条件。这种类型的错误需要仔细检查函数的递归调用逻辑和参数传递规则。

### 2.2 错误诊断方法

#### 2.2.1 日志分析与跟踪

为了诊断和调试递归函数中的错误，日志分析是一种非常重要的手段。通过在递归函数的关键位置添加日志记录，开发者可以追踪函数的执行路径，验证参数值，并监控程序状态。

代码示例：

import logging

logging.basicConfig(level=***)

def logging_recursive_function(n):
    ***(f"Entering recursive_function with n={n}")
    if n <= 0:
        ***("Base case reached")
        return 1
    else:
        result = n * logging_recursive_function(n - 1)
        ***(f"Returning result: {result}")
        return result

logging_recursive_function(5)

逻辑分析与参数说明：
在上述Python示例中，通过使用`logging`模块，我们可以记录递归函数的执行过程，包括每次函数调用的输入参数和返回结果。这有助于发现递归过程中的异常行为，特别是在复杂的递归逻辑中。

#### 2.2.2 异常捕获与堆栈跟踪

在递归函数中有效地使用异常捕获机制可以帮助开发者定位和诊断错误。异常处理通常与堆栈跟踪结合使用，以获取详细的错误发生上下文。

代码示例：

def exception_catching_function(n):
    try:
        if n == 0:
            raise ValueError("n must be greater than 0")
        return n * exception_catching_function(n - 1)
    except Exception as e:
        print(f"Caught exception: {e}")
        import traceback
        traceback.print_exc()  # 打印堆栈跟踪信息

exception_catching_function(-1)

逻辑分析与参数说明：
在上述示例中，当传入的参数`n`为0时，我们手动抛出一个`ValueError`异常，并在`except`块中捕获它。通过调用`traceback.print_exc()`，我们能够打印出完整的堆栈跟踪信息，这对于理解和调试深层递归中的错误非常有帮助。

# 3. 递归错误的预防与控制

## 3.1 设计模式在递归错误预防中的应用

### 3.1.1 分治策略与递归优化

分治策略是递归设计中一种常见的模式，它将大问题分解为小问题，并递归地解决这些子问题。这种方法有助于简化复杂问题的求解过程，并能有效控制递归错误的发生。以下是通过分治策略进行递归优化的一些关键点：

1. **问题分解**：将复杂问题分解成若干个可独立求解的子问题。确保每个子问题足够小，以减少递归深度。
2. **递归函数优化**：对于可以重用子问题解的情况，使用记忆化技术存储已经解决的子问题，避免重复计算。
3. **终止条件设置**：合理设置递归函数的终止条件，保证每一次递归调用都能最终停止，防止无限递归的发生。

下面是一个简单的递归函数优化示例，使用Python编写了一个斐波那契数列的计算函数，并应用了记忆化技术：

# 记忆化斐波那契数列计算
memo = {}

def fibonacci(n):
    if n in memo:
        return memo[n]
    if n <= 1:
        return n
    memo[n] = fibonacci(n-1) + fibonacci(n-2)
    return memo[n]

# 使用示例
print(fibonacci(10))  # 输出 55

通过使用记忆化技术，我们减少了递归调用的次数，并有效防止了重复计算，这显著提高了计算效率。

### 3.1.2 尾递归的转换与实现

尾递归是另一种优化递归的方法，指的是在递归函数的最后一个操作是递归调用的情形。尾递归可以被编译器优化为迭代形式，减少栈空间的使用，从而有效预防栈溢出问题。

要实现尾递归优化，需要确保递归调用是函数的最后一个操作，并且当前的状态不需要在递归调用之后恢复。下面是一个简单的尾递归示例：

def tail_recursive_f