递归与回溯的策略指南：数据结构中解题的深度分析

# 1. 递归与回溯的基本概念

## 1.1 递归与回溯的重要性
递归与回溯是计算机科学中的两个核心概念，它们在算法设计中扮演着重要角色。递归是一种解决问题的方法，它将问题分解为更小的、易于管理的子问题，通过自我调用来求解。而回溯，则是一种系统地探索所有可能的解决方案的策略，直到找到所需的答案或遍历所有可能性为止。

## 1.2 递归的定义和特点
递归是一种编程技术，允许函数调用自身。它主要依赖于两个关键要素：基本情况和递归情况。基本情况定义了递归何时停止，而递归情况则将问题分解成更小的子问题。递归的实现依赖于函数的调用栈，因此理解其工作原理对于设计高效算法至关重要。

## 1.3 回溯的定义和应用
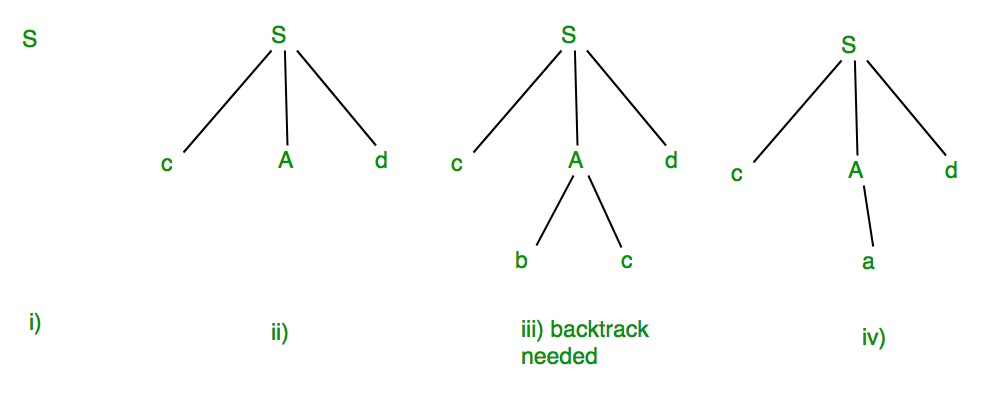
回溯算法是一种通过探索所有潜在可能性来解决优化问题的方法。它在解决诸如组合、排列和子集问题时尤为有用。回溯算法通过深度优先搜索来逐步构建解决方案，当发现当前构建的路径不可能达到有效解时，它会“回溯”到上一个决策点，并尝试不同的可能性。在许多问题中，回溯是找到解决方案或证明问题不可解的唯一方法。

# 2. 递归策略的理论与实现

## 2.1 递归函数的定义和原理
### 2.1.1 递归函数的工作机制
递归函数是一种调用自身的函数，它通过分解问题为更小子问题的方式，逐步深入到问题的核心。在每次函数调用中，子问题在形式上与原始问题相似，但规模更小。递归的关键在于定义两个基本元素：基本情况（也称为终止条件）和递归情况。

基本情况是递归能够停止继续分解并开始返回结果的点。如果没有基本情况，递归函数将无限地调用自己，最终导致栈溢出错误。递归情况则描述了如何将问题分解为子问题，并应用相同的函数来解决这些子问题。

递归函数的工作流程可以用以下步骤概括：
1. 检查基本情况。如果满足，则直接返回结果。
2. 若不满足基本情况，则将问题分解为一个或多个子问题。
3. 递归地对子问题调用相同的函数。
4. 等待子问题的解决结果，并将其组合以得出当前问题的解答。
5. 返回当前问题的结果。

### 2.1.2 递归三要素与递归终止条件

递归三要素通常指的是：
1. **边界条件**：这是递归调用停止的条件，也是递归函数必须明确指定的部分。没有边界条件，递归函数将无止境地执行下去。
2. **递归模式**：定义了如何通过递归调用来缩小问题规模。
3. **问题规模**：在每一次递归调用中，问题的规模都会有所减少，直到达到边界条件。

递归终止条件是确保递归能够在有限步骤内完成的关键。这通常是在问题规模缩小到最基本形式时达到的，即当问题不能再被分解为更小的问题时。终止条件必须满足以下两个特点：
- **可达到性**：必须能够通过一系列递归调用达到终止条件。
- **唯一性**：在每次递归调用过程中，只存在一个唯一的终止条件，以避免产生歧义或重复的递归调用。

例如，在计算阶乘的递归函数中：

def factorial(n):
    # 终止条件：当n等于0时，返回1，因为0! = 1
    if n == 0:
        return 1
    # 递归模式：n! = n * (n-1)!
    else:
        return n * factorial(n-1)

在这个例子中，终止条件是`n == 0`，递归模式是通过`n * factorial(n-1)`来缩小问题规模。

## 2.2 递归策略在问题解决中的应用
### 2.2.1 直接递归与间接递归的场景分析

直接递归是最常见和最简单的递归形式，函数直接调用自己。间接递归则涉及到两个或多个函数互相调用，形成一个调用链。尽管间接递归在结构上更复杂，但其本质上仍然是递归调用的一种表现形式。

直接递归的场景相对直观，例如在树的深度优先遍历中，我们直接递归地访问树的节点。在斐波那契数列的计算中，也是一个典型的直接递归例子。

间接递归的例子可能包括A函数调用B函数，B函数又调用C函数，C函数最后调用A函数。这种调用链条让递归过程更加复杂，要求设计者对程序的运行逻辑有清晰的认识，避免产生无限循环或重复的递归调用。

例如：

def A(n):
    if n == 0:
        return 1
    else:
        return B(n-1)

def B(n):
    if n == 0:
        return 2
    else:
        return A(n-1)

print(A(5)) # 这将输出间接递归的调用结果

在这个示例中，函数A和函数B相互递归调用，形成了间接递归。

### 2.2.2 递归解决树和图的遍历问题

递归是解决树和图这类数据结构问题的常用方法，特别是在树的深度优先遍历（DFS）和图的深度优先搜索中。递归能够自然地表达遍历过程中，节点的探索、访问和回溯。

在树的DFS中，我们通常从根节点开始，递归地遍历左子树和右子树。在图的DFS中，对于一个给定的节点，我们访问它未被访问过的邻居节点，并对这些邻居节点递归执行相同的操作。

例如，在树的DFS中：

class TreeNode:
    def __init__(self, value):
        self.val = value
        self.left = None
        self.right = None

def DFS(node):
    if node is None:
        return
    # 处理当前节点（例如打印节点的值）
    print(node.val)
    # 递归遍历左子树
    DFS(node.left)
    # 递归遍历右子树
    DFS(node.right)

# 构建一个简单的树结构
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)

# 执行深度优先遍历
DFS(root)

在这个树结构的深度优先遍历中，我们递归地访问每个节点及其子节点，直到所有节点都被访问过。

## 2.3 递归算法的效率分析与优化
### 2.3.1 时间复杂度和空间复杂度的评估

递归算法的时间复杂度和空间复杂度与递归树的深度有直接关系。时间复杂度衡量算法执行需要的总时间，通常通过递归调用的次数来评估。空间复杂度衡量算法执行需要的存储空间，通常与递归深度（调用栈的深度）成正比。

时间复杂度的评估要考虑以下几点：
- 基本操作（如递归调用）的次数。
- 每次递归调用中子问题的规模。
- 递归树的深度，即递归调用的最大层数。

空间复杂度的评估通常较为直接，因为它仅与递归深度相关，即系统为每次递归调用分配的栈空间。

例如，计算阶乘的递归算法：

def factorial(n):
    if n <= 1:
        return 1
    return n * factorial(n-1)

这个阶乘算法的时间复杂度是O(n)，因为递归树的深度是n。空间复杂度也是O(n)，因为需要n层递归调用来存储栈信息。

### 2.3.2 记忆化搜索技术及其优化效果

记忆化搜索是一种递归优化技术，它存储了子问题的解，这样当下次遇到相同的子问题时，可以直接使用存储的解，而不是重新计算，从而避免了大量重复计算，显著提高效率。

记忆化搜索通常使用一个数据结构（如字典或数组）来保存已经解决的子问题的解。这种方法特别适用于那些有大量重叠子问题的递归问题，比如斐波那契数列的计算。

例如，在斐波那契数列计算中，使用记忆化：

def memoize(f):
    memo = {}
    def helper(x):
        if x not in memo:            
            memo[x] = f(x)
        return memo[x]
    return helper

@memoize
def fib(n):
    if n < 2:
        return n
    return fib(n-1) + fib(n-2)

print(fib(10)) # 这将输出较快的结果，因为使用了记忆化

在这个例子中，我们使用了`memoize`装饰器来缓存计算过的斐波那契数。这样，对于每一个计算过的数字，我们都不需要再次递归计算，大大减少了计算次数，提高了效率。

# 3. 回溯算法的理论与实践

## 3.1 回溯算法概述

### 3.1.1 回溯算法的核心思想和框架

回溯算法是一类通过探索所有可能的候选解来找出所有解的算法，如果候选解被确认不是一个解（或者至少不是最后一个解），算法会通过在上一步进行一些变化来丢弃该解，即回溯并且再次尝试。这种走不通就回退再尝试其它路径的算法可以形象地称为“试错法”。其基本思想是：从一条路往前走，能进则进，不能进则退回来另寻别路。

回溯算法的核心框架可以总结为以下伪代码：

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return
    for 选择 in 选择列表:
        做选择
        back