数据结构中的递归算法：原理、设计与优化的全面教程

# 1. 递归算法的概念与重要性

## 1.1 递归算法的定义
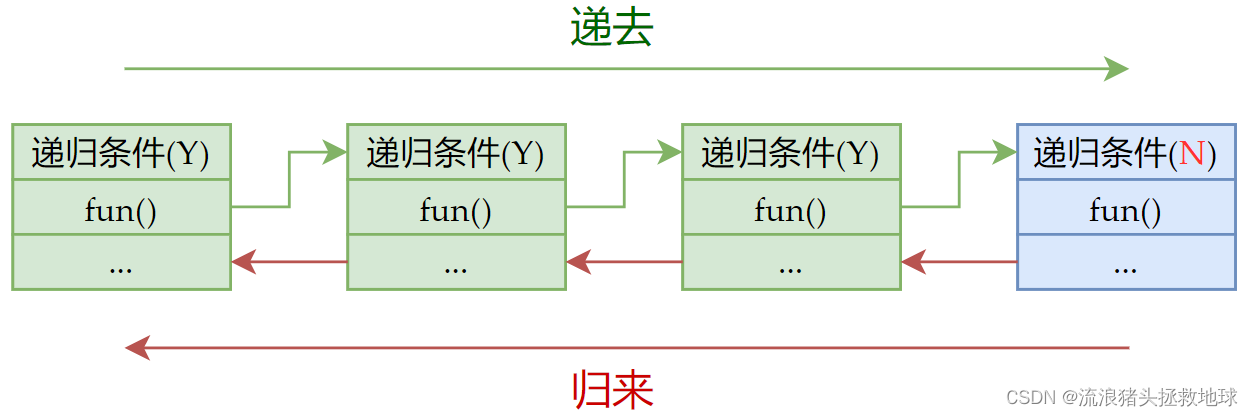
递归算法是一种通过函数自身调用自身来解决问题的编程技术。它允许一个函数反复地调用自己，以解决问题的子问题。递归通常用于处理可分解为相似子问题的问题，并且每个子问题都可以通过相同的算法来解决。递归的关键在于识别递归情况和基本情况，基本情况代表了最简单的问题实例，可以无需进一步递归即可解决。

## 1.2 递归算法的重要性
递归算法在计算机科学领域拥有不可替代的地位，其重要性体现在多个方面。首先，递归为解决复杂问题提供了一种直观且简洁的解决方案，尤其是在树形结构和图的遍历中。其次，递归思想是算法设计中的核心概念，许多高级算法如分治算法、动态规划等，都建立在递归的基础上。此外，递归在函数式编程语言中是基本构造之一，为编程提供了强大的表达力。理解递归不仅对编写高效的程序至关重要，也有助于培养深厚的算法理解能力。

# 2. 递归算法的理论基础

### 2.1 递归的定义与数学基础
递归是一种常见的算法设计方法，它允许函数调用自身来解决问题。递归在数学中有着深远的根源，尤其是在函数论和数理逻辑领域。为了更深入理解递归算法，我们首先需要探究它的基本定义和数学基础。

#### 2.1.1 递归的定义
递归函数是直接或间接调用自身的函数。在编程中，递归通常用来简化问题的解决方法。基本思路是将大问题分解为更小的问题，而这些小问题与原始问题性质相同，可以使用同样的解决方法。

def factorial(n):
    if n == 0: 
        return 1
    else: 
        return n * factorial(n-1)

在上述Python代码中，`factorial`函数通过递归方式计算了阶乘。当`n`等于0时，终止条件触发，函数返回1；否则，函数将调用自身计算`n-1`的阶乘，并将结果与`n`相乘。

#### 2.1.2 递归与数学归纳法
数学归纳法是递归的重要基础，它是一系列递推式，用来证明数学命题对所有自然数成立。递归算法在解决实际问题时也常常利用归纳法的思想，通过逐步证明每个步骤的正确性来保证整个过程的有效性。

### 2.2 递归算法的结构分析
递归算法的结构通常包括基本情况和递归情况。为了进一步细化问题，我们讨论这两种情况在递归树和分治策略中的应用。

#### 2.2.1 基本情况与递归情况
基本情况（Base Case）是递归终止的条件，而递归情况（Recursive Case）则是在不满足终止条件时，函数如何分解并解决子问题的逻辑。

graph TD
    A[递归函数] -->|终止条件| B[基本情况]
    A -->|递归分解| C[递归情况]
    C --> D[进一步递归]
    D --> B
    D -->|解决更多子问题| E[进一步递归]

#### 2.2.2 递归树和分治策略
在递归树的模型中，每次递归调用都会产生一棵新的子树。分治策略是一种解决问题的方法，它将原问题分解成若干子问题，递归地解决这些子问题，并将结果合并以得到原问题的解。

### 2.3 递归算法的理论模型
了解了递归算法的基本结构后，我们需要讨论不同类型的递归模型，以及它们的时间和空间复杂度。

#### 2.3.1 递归模型的类型
递归模型主要分为线性递归和树形递归，其中线性递归有一个调用栈，而树形递归有多个调用栈，树形递归的复杂度往往更高。

#### 2.3.2 时间复杂度与空间复杂度分析
递归算法的时间复杂度通常与递归的深度和每次递归解决子问题的复杂度有关。空间复杂度则涉及递归调用的栈空间，包括所有递归活动记录的总空间。

- 时间复杂度: O(n) (n为问题规模)
- 空间复杂度: O(n) (假设每次递归调用栈空间为O(1))

递归算法的理论基础为我们提供了解决问题的数学工具和理论模型。在下一章节中，我们将继续深入讨论递归算法的设计技巧和应用方法。

# 3. 递归算法的设计技巧

## 3.1 递归算法的设计原则

### 3.1.1 确定递归终止条件
递归算法设计中的首要步骤是确定递归的终止条件。没有终止条件，递归函数将无限调用自身，最终导致栈溢出错误。终止条件是递归结束的基准情况，它定义了递归算法何时停止递归并返回结果。在实际编程中，终止条件通常与问题的最基本情况相对应。

例如，在计算阶乘的递归函数中，终止条件可以是当输入参数为1时（阶乘的基本定义）。在实现这个函数时，我们会这样定义终止条件：

def factorial(n):
    if n == 1:
        return 1
    else:
        return n * factorial(n-1)

上述代码中，`if n == 1` 就是终止条件。一旦 `n` 达到1，函数不再进行递归调用，直接返回1。如果 `n` 大于1，则函数通过 `return n * factorial(n-1)` 继续递归调用自身。

### 3.1.2 选择合适的递归分解
递归分解是将原问题分解为若干个规模较小的子问题的过程。在选择递归分解策略时，需要确保子问题能够更简单地解决，并且最终能够达到终止条件。在实际应用中，递归分解可以按照数据结构的不同进行分解，例如对于数组或列表，分解策略可以是去除第一个元素；对于树结构，则可以是处理子节点等。

分解策略的选择依赖于问题本身的性质。例如，二分搜索算法的递归分解是将搜索区间分成两部分，然后在其中一部分上继续执行二分搜索。这不仅保证了问题的规模逐步减小，而且确保了搜索范围的逐步精确定位。

def binary_search(arr, low, high, x):
    if high >= low:
        mid = (high + low) // 2
        if arr[mid] == x:
            return mid
        elif arr[mid] > x:
            return binary_search(arr, low, mid-1, x)
        else:
            return binary_search(arr, mid+1, high, x)
    else:
        return -1

在上述代码中，每次递归调用都以 `mid` 为界限将数组分成两半，选择包含 `x` 的那半进行进一步搜索。

## 3.2 递归与迭代的对比

### 3.2.1 迭代算法的特点
迭代算法是一种通过重复执行一定步骤来达到目标的算法，它利用循环结构（如 `while` 或 `for` 循环）来重复执行代码块，直至满足终止条件。迭代算法的特点在于其执行的控制结构是顺序的，易于理解和实现。相对于递归，迭代通常会减少函数调用的开销，因为它避免了栈的使用。

举例来说，使用迭代方式计算阶乘的代码如下：

def factorial_iterative(n):
    result = 1
    for i in range(2, n+1):
        result *= i
    return result

### 3.2.2 递归与迭代的转换技巧
递归算法与迭代算法各有优势。在很多情况下，可以将一种形式转换为另一种形式。递归转换为迭代需要实现一个循环结构，并在其中模拟递归调用的逻辑。这种转换有助于减少由于递归调用栈过大而产生的栈溢出问题。

以计算斐波那契数列为例，递归实现如下：