数据结构与算法课程中的递归教学：策略与实践

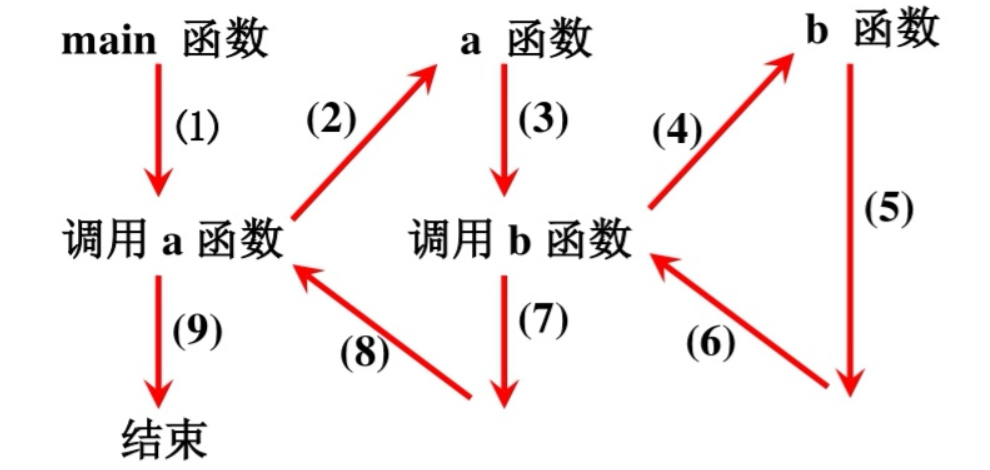
# 1. 递归概念的理论基础

递归是计算机科学中一种重要的算法设计范式，它允许一个函数直接或间接地调用自身。在这一章中，我们将从理论的角度探讨递归的概念，了解递归的核心要素，并介绍递归的基本工作原理。理解递归的概念，是掌握递归算法策略和优化的第一步。

## 1.1 递归的定义和基本原理

递归函数包含两个主要部分：基准情形（base case）和递归情形（recursive case）。基准情形是递归调用停止的条件，而递归情形则通过函数自身调用，逐步逼近基准情形。递归能够将复杂的问题分解为规模更小的相似问题，直至达到最简单的情况，使得问题变得易于解决。

## 1.2 递归在算法设计中的作用

递归作为一种算法设计方法，广泛应用于各种问题的求解中，比如树和图的遍历、分治算法、排序和搜索算法等。递归算法通常具有良好的数学美感，逻辑清晰，代码简洁。然而，理解递归需要具备一定的抽象思维能力，因为递归函数往往需要在没有具体实例的情况下理解其工作过程。

通过本章的介绍，读者将对递归有一个基础性的理解，并为后续章节中递归算法的深入学习打下坚实的基础。

# 2. 递归算法的策略解析

在深入探讨递归算法的策略之前，我们需要建立对递归的全面理解。递归是算法设计中一种重要的技术手段，它允许算法自我调用，从而解决更复杂的问题。递归算法通常基于两个基本要素：边界条件和递推关系。边界条件定义了递归的结束点，而递推关系则描述了问题是如何分解成更小的子问题，以及如何将这些子问题的解组合成整个问题的解。

### 2.1 递归算法设计原则

#### 2.1.1 基本要素：边界条件与递推关系

在设计递归算法时，首先需要确定边界条件，它指导算法何时停止递归。例如，在计算阶乘的递归函数中，边界条件可能是 n 等于 1。当 n 大于 1 时，函数将递归调用自身来计算 (n-1)!，然后用结果乘以 n 来得到 n!。

递推关系是递归算法核心，它定义了问题如何分解。例如，对于计算数列的第 n 项的递归算法，递推关系可能是 f(n) = f(n-1) + f(n-2)，这就是著名的斐波那契数列。

#### 2.1.2 分治法与递归树模型

分治法是递归算法的一种典型策略，通过将大问题分解为小问题，解决小问题后，再合并结果来解决原问题。递归树模型是分析分治算法复杂度的直观工具，通过树的深度和分支数可以推导出算法的时间复杂度。

### 2.2 递归与动态规划

#### 2.2.1 动态规划的递归实现

动态规划（DP）是解决优化问题的算法策略，常用于在多阶段决策过程中找到最优解。递归实现动态规划时，可以通过将问题分解为重叠的子问题，并保存这些子问题的解来避免重复计算，从而提高效率。

#### 2.2.2 递归与记忆化搜索

记忆化搜索是一种优化递归过程的技术，它通过存储已经计算过的子问题的解，使得当同一个子问题再次出现时，可以直接使用存储的解，而不是重新计算。这显著减少了计算量，并提高了递归算法的效率。

### 2.3 递归的优化策略

#### 2.3.1 尾递归的原理与应用

尾递归是一种特殊的递归形式，其中递归调用是函数体中的最后一个操作。某些编译器或解释器可以对此进行优化，将递归转化为迭代，从而减少栈空间的使用。这对于防止深度递归导致的栈溢出问题至关重要。

#### 2.3.2 递归深度控制与栈优化

递归深度控制是为了防止程序崩溃而设置的。在一些语言中，可以通过设置栈的大小或深度限制来避免栈溢出。在其他语言中，可以通过非递归的方式，如使用显式的栈数据结构来模拟递归过程，从而更有效地控制内存使用。

在接下来的章节中，我们将详细探讨如何在数据结构中应用递归，并通过具体实例来分析递归的实现和优化策略。在掌握了递归算法的策略解析后，让我们继续深入到数据结构中的递归应用实例。

# 3. 递归在数据结构中的应用实例

## 3.1 树与二叉树的递归遍历

在计算机科学领域，树结构是最为重要的数据结构之一，尤其是二叉树，它是许多复杂数据结构和算法的基础。递归遍历是处理树形数据结构的常用方法之一，它能够以一种简洁而直观的方式遍历树的每一个节点。

### 3.1.1 前序、中序和后序遍历的递归实现

前序、中序和后序遍历是树结构中三种基本的递归遍历方法。每种遍历方式都关注于节点值输出的顺序。下面通过递归实现这三种遍历方法。

class TreeNode:
    def __init__(self, value):
        self.val = value
        self.left = None
        self.right = None

def preorder_traversal(root):
    if root is None:
        return []
    return [root.val] + preorder_traversal(root.left) + preorder_traversal(root.right)

def inorder_traversal(root):
    if root is None:
        return []
    return inorder_traversal(root.left) + [root.val] + inorder_traversal(root.right)

def postorder_traversal(root):
    if root is None:
        return []
    return postorder_traversal(root.left) + postorder_traversal(root.right) + [root.val]

上述代码中，我们首先定义了`TreeNode`类来表示树的节点。然后分别实现了前序、中序和后序遍历的递归函数。需要注意的是，递归函数的终止条件是当前节点为空，在该条件满足时函数返回空列表。否则，函数将递归调用自身，分别访问左右子树，并将结果合并起来。

### 3.1.2 递归解构复杂树结构

递归不仅仅是遍历树的一种方法，也可以用于解构复杂树结构。在处理诸如表达式树或文件系统这样的复杂结构时，递归可以简化代码并使其更加易于理解。

def tree_to_list(root):
    if root is None:
        return []
    return [root.val] + tree_to_list(root.left) + tree_to_list(root.right)

# 假设我们有如下复杂的树结构
#        1
#       / \
#      2   3
#     / \   \
#    4   5   6

root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.