递归的递进式掌握：解决复杂问题的数据结构策略

# 1. 递归的概念与重要性

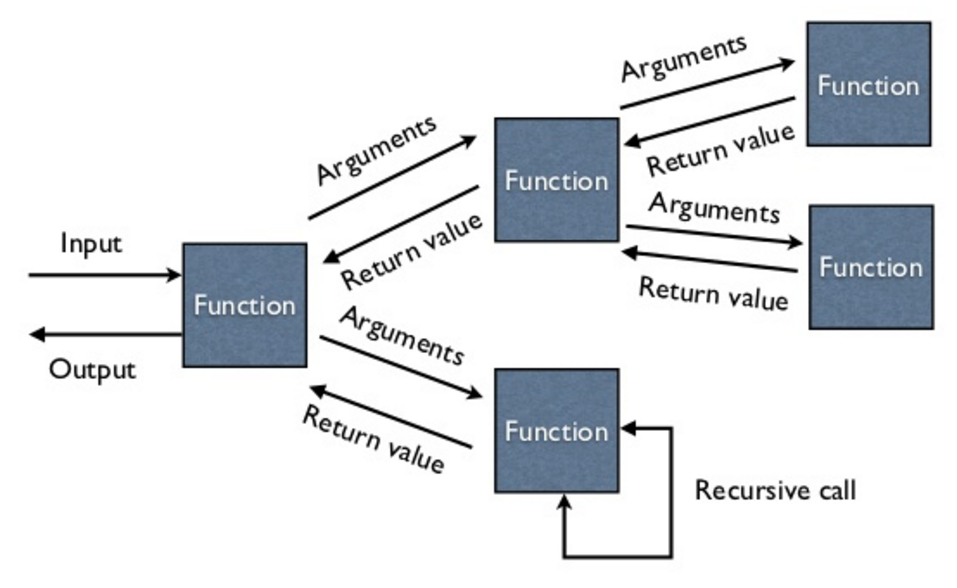
递归是一种在程序设计中常用的算法思想，它的核心在于“自己调用自己”。递归的原理简单而强大，它允许我们将复杂问题分解为更小、更容易解决的子问题。理解递归不仅能够帮助我们解决特定的编程问题，而且对培养编程思维有着不可忽视的作用。

递归的重要性体现在多个方面。首先，它在解决某些类型的问题时，如树或图的遍历、组合问题等，提供了一种直观和简洁的解决方案。其次，递归是学习动态规划、分治算法等高级技术的基础，因此掌握递归对深入理解计算机科学原理至关重要。

然而，递归也有其局限性和风险，比如可能导致栈溢出。因此，深入理解递归的工作原理及其应用场景，对每个IT从业者来说都是必不可少的知识储备。接下来的章节，我们将从理论和实践两个维度，探索递归的奥秘，揭示其在现代编程中的重要角色。

# 2. 递归算法的理论基础

## 2.1 递归的数学模型

### 2.1.1 递归函数的定义与性质

递归函数是在定义中直接或间接调用自身的函数。它们的基本特性是能够将问题分解为更小的、相似的子问题。递归函数的定义通常包括两个主要部分：基本情况（base case）和递归情况（recursive case）。基本情况是函数的最简单形式，可以直接解决而不需要进一步的递归调用。递归情况则将问题分解为更小的子问题，并调用自身以解决这些子问题。

从数学的角度来看，递归函数的性质可以通过递推关系来描述。递推关系定义了函数在某一点的值与它在其它点的值之间的关系。例如，阶乘函数的递推关系可以表示为：

n! = n * (n-1)!

其中 `1! = 1` 是基本情况。

### 2.1.2 递归与数学归纳法

递归函数和数学归纳法有着紧密的联系。数学归纳法用于证明数学命题对所有自然数成立，包括两个步骤：基础步骤（验证最小的自然数，通常是1）和归纳步骤（假设命题对某个自然数k成立，证明它对k+1也成立）。

递归函数的执行过程与数学归纳法相似。每次递归调用都是一个归纳步骤，它基于对较小规模问题的解决方案来构建当前规模问题的解决方案。而基本情况相当于归纳法中的基础步骤，是递归展开的终止条件。

### 2.2 递归算法的复杂度分析

#### 2.2.1 时间复杂度的计算方法

时间复杂度是衡量算法运行时间的一个重要指标。在递归算法中，时间复杂度的计算需要考虑递归调用的次数以及每次调用完成所需的基本操作数。

以二叉树的遍历为例，如果每个节点都需要处理一次，那么时间复杂度是 O(n)，其中n是树中的节点数。但是，如果递归函数中存在重复计算，例如在没有适当缓存机制的情况下多次计算相同的子问题，则时间复杂度会急剧上升。

#### 2.2.2 空间复杂度的考量

空间复杂度衡量的是算法在运行过程中临时占用存储空间的大小。递归算法的空间复杂度主要取决于递归调用的深度，即递归栈的大小。每个递归调用都需要在栈上存储局部变量和返回地址，因此栈的大小将直接决定空间复杂度。

例如，对于简单的递归函数，其空间复杂度为 O(d)，其中d是递归的最大深度。对于需要额外空间存储子问题解的递归算法，空间复杂度还需要考虑这部分存储空间。

### 2.3 递归与分治策略

#### 2.3.1 分治算法的基本原理

分治算法是一种将大问题分解为小问题、分别解决这些小问题，然后再合并结果来解决原始问题的算法策略。递归是实现分治策略的一种自然方式。

分治算法通常遵循“分-治-合”的步骤：
1. **分**：将问题分解为若干规模较小的同类问题。
2. **治**：递归解决这些子问题。
3. **合**：将子问题的解合并成原始问题的解。

#### 2.3.2 递归实现分治策略的案例分析

以快速排序（Quick Sort）为例，快速排序是一个典型的分治递归算法。快速排序的基本步骤是：
1. 选择一个基准值（pivot）。
2. 将数组分为两部分，一部分包含小于基准值的元素，另一部分包含大于基准值的元素。
3. 递归地对这两部分进行快速排序。
4. 合并排序后的数组。

快速排序的平均时间复杂度是 O(n log n)，但由于递归调用的存在，其空间复杂度为 O(log n)，主要由递归调用栈的深度决定。

在分析递归算法的复杂度时，通常会使用递归树来可视化递归调用的过程。递归树的每一层代表递归的深度，节点代表递归调用。通过递归树，我们可以更直观地分析算法的时间和空间复杂度。

通过本章节的介绍，我们深入理解了递归算法的理论基础，包括其数学模型、复杂度分析以及与分治策略的关系。下一章我们将探讨递归在数据结构中的应用，进一步展示递归算法的实践价值。

# 3. 递归在数据结构中的应用

递归是一种强大的编程技巧，它允许函数调用自身来解决问题。在数据结构中，递归的应用尤为广泛，尤其是在树形结构和图的处理中。本章节将深入探讨递归在数据结构不同应用场景中的原理和实现细节。

## 3.1 树形结构的递归遍历

### 3.1.1 二叉树的递归遍历算法

二叉树是最常见的树形结构之一，其递归遍历算法是计算机科学中的经典问题。二叉树的递归遍历主要有三种：前序遍历、中序遍历和后序遍历。

在前序遍历中，我们首先访问根节点，然后递归遍历左子树，最后递归遍历右子树。中序遍历则是先遍历左子树，再访问根节点，最后遍历右子树。后序遍历是先遍历左子树，再遍历右子树，最后访问根节点。

下面是一个简单的二叉树节点的定义以及前序遍历的递归实现代码示例：

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

def preorderTraversal(root):
    if not root:
        return []
    return [root.val] + preorderTraversal(root.left) + preorderTraversal(root.right)

# 假设有一个二叉树如下：
#       1
#      / \
#     2   3
#    / \   \
#   4   5   6

# 预期输出结果为: [1, 2, 4, 5, 3, 6]

前序遍历的递归函数从根节点开始，按照前序遍历的顺序访问节点，对于每个节点，将其值添加到结果列表中，然后对其左子树和右子树进行同样的操作。

### 3.1.2 多叉树与B树的递归策略

多叉树的递归遍历与二叉树类似，区别在于每个节点可能有多个子节点。递归时需要对每个子节点进行遍历，而不是仅限于两个子节点。

B树是一种自平衡的树数据结构，它维护了数据的排序并且允许搜索、顺序访问、插入和删除操作。B树的递归策略通常涉及到在节点中递归地搜索给定值，或者在节点分裂时递归地处理。

在B树中，节点可以有多个子节点，通常使用数组来存储子节点的指针。在插入或删除节点时，可能会涉及节点的合并或分裂，这时需要递归地处理以保证B树的性质。

## 3.2 图的递归搜索算法

### 3.2.1 深度优先搜索(DFS)

深度优先搜索(DFS)是一种用于遍历或搜索树或图的算法。在图中，DFS从一个节点开始，尽可能深地沿着每个分支走到底，然后回溯继续搜索。

递归是实现DFS的一种自然方式，因为DFS本身就可以看作是对图的一个递归探索过程。递归的DFS会访问当前节点，然后对其每个未访问的邻居节点进行DFS。

下面是DFS的一个基本递归实现示例：

def DFS(graph, start, visited=None):
    if visited is None:
        visited = set()
    visited.add(start)
    print(start)
    for next in graph[start] - visited:
        DFS(graph, next, visited)
    return visited

# 示例图的邻接表表示
graph = {
    'A': {'B', 'C'},
    'B': {'A', 'D', 'E'},
    'C': {'A', 'F'},
    'D': {'B'},
    'E': {'B', 'F'},
    'F': {'C', 'E'}
}

# 预期输出结果为: A B D E F C

### 3.2.2 广度优先搜索(BFS)

与DFS递归方式不同，广度优先搜索(BFS)通常使用队列来实现。BFS从一个节点开始，访问其所有邻居，然后再对其邻居的邻居进行访问，依此类推。

尽管BFS通常使用迭代而非递归实现，但递归版本的BFS也是可能的。在递归版本中，每次递归调用会处理一个层级的所有节点。

下面是BFS递归实现的一个示例：

def BFS(graph, start, visited=None):
    if visited is None:
        visited = set()
    queue = [start]
    while queue:
        node = queue.pop(0)
        if node not in visited:
            print(node)
            visited.add(node)
            queue.extend(graph[node] - visited)
    return visited

# 示例图的邻接表表示
graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E']
}

# 预期输出结果为: A B C D E F

## 3.3 递归在字符串处理中的应用

### 3.3.1 字符串匹配问题的递归解法

字符串匹配问题是指在一个文本字符串中查找一个模式串出现的位置。递归方法可以用来实现一些字符串匹配算法，例如递归实现的字符串搜索算法。

一个简单的递归字符串匹配算法示例：

def recursive_search(txt, pat):
    if pat == "":
        return 0  # empty pattern matches at the beginning of txt
    elif txt == "":
        return -1  # empty text doesn't match
    else:
        return first_match(txt, pat)  # check for a match and recurse

def first_match(txt, pat):
    if pat[0] == txt[0]:
        return 0  # the first characters match
    else:
        return 1 + first_match(txt[1:], pat)  # advance txt or pattern

# Example usage:
# txt = "abcxabcxyabcz"
# pat = "abcxy"
# Expected outp