数据结构中的递归魅力：从论文视角看问题解决之道

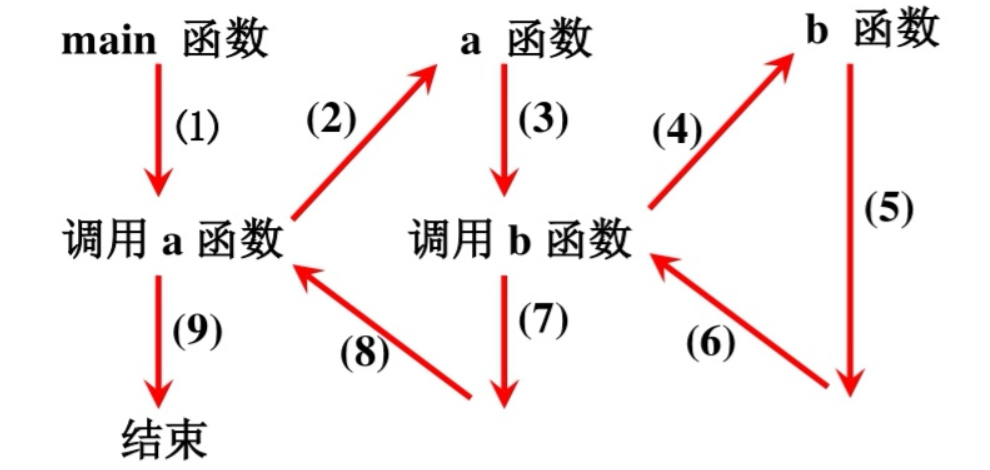
# 1. 递归的本质与重要性

## 1.1 理解递归的概念
递归是一种编程技巧，它允许函数调用自身来解决问题。递归方法的关键在于将大问题分解成小问题，直至达到一个简单得可以直接解决的基准情形。这一过程形成一个递归调用栈，不断深入直到问题可以解决为止。

## 1.2 递归的重要性
递归方法的重要性体现在其简单和强大的逻辑表达上，特别是在处理具有自然层次或递归子结构的问题，如树的遍历、分治算法等。它通过减少代码的重复和增强可读性，简化了复杂问题的解决方案。

## 1.3 递归的典型应用场景
递归广泛应用于解决诸如文件系统遍历、汉诺塔问题、算法排序(如快速排序)等具有天然递归结构的问题。它还可以在解决分治法策略适用的问题时发挥巨大作用，如大整数的快速乘法、图形渲染等。

// 示例：计算阶乘的递归函数
function factorial(n) {
    if (n <= 1) return 1; // 基准情形
    return n * factorial(n - 1); // 递推关系
}

递归虽然强大，但过度使用可能导致性能问题，如栈溢出和不必要的计算。因此，在实际应用中需要对递归进行优化。在后续章节中，我们将深入了解递归的理论基础和应用场景，以及如何应对递归带来的挑战。

# 2. 递归理论基础与算法原理

## 2.1 递归的数学定义

### 2.1.1 函数自引用的概念

递归是一种在数学、逻辑学、计算机科学等领域广泛应用的方法论，它允许函数调用自身来解决问题。函数自引用的概念是理解递归的基石。在数学中，递归函数是通过定义规则和初始条件来构建的。例如，一个数列的每一项由前一项或前几项计算得出，这种方式可以看作是一种简单的递归关系。

# 一个简单的阶乘函数，展示了递归的自引用概念
def factorial(n):
    if n == 0:  # 基准情形
        return 1
    else:
        return n * factorial(n-1)  # 自引用调用

在这个阶乘函数的例子中，`factorial` 函数通过自引用的方式调用自身来计算一个数的阶乘。递归算法通常需要定义基准情形（Base Case），它是递归停止的条件，防止无限递归的发生。

### 2.1.2 递归的基准情形与递推关系

递归算法的基准情形是函数中不调用自身的那部分逻辑，它是递归终止的条件。递推关系（或称为递归方程）定义了如何通过较小的实例来构建较大实例的过程。正确地定义基准情形和递推关系是递归算法设计的关键。

# 斐波那契数列的递归实现，展示了基准情形与递推关系
def fibonacci(n):
    if n <= 1:  # 基准情形
        return n
    else:
        return fibonacci(n-1) + fibonacci(n-2)  # 递推关系

在斐波那契数列的递归实现中，`n <= 1` 是基准情形，而 `fibonacci(n-1) + fibonacci(n-2)` 则描述了递推关系。每一项是由前两项相加而成。

## 2.2 递归与迭代的关系

### 2.2.1 递归与迭代的对比分析

递归和迭代是两种常见的算法设计技术。递归是通过函数自身调用自身来解决问题，而迭代是通过重复使用循环结构来达到相同的目的。在某些情况下，递归和迭代可以互相转换，但它们在逻辑清晰度、性能和内存消耗等方面各有利弊。

### 2.2.2 迭代转递归的转换技巧

将迭代算法转换为递归算法通常涉及确定递归函数的基本情况和递归步骤。递归函数需要保持等价于原迭代算法的逻辑，但使用自引用的方式来重复计算。

# 迭代算法转递归算法的示例：求和
def iterative_sum(lst):
    total = 0
    for num in lst:
        total += num
    return total

def recursive_sum(lst):
    if not lst:
        return 0
    else:
        return lst[0] + recursive_sum(lst[1:])

在上述代码中，`iterative_sum` 函数使用了一个循环来计算列表中所有数字的总和。而 `recursive_sum` 函数通过递归达到了同样的目的。

## 2.3 递归算法的复杂度分析

### 2.3.1 时间复杂度和空间复杂度

递归算法的时间复杂度和空间复杂度分析是理解其性能的关键。时间复杂度描述了算法执行时间与输入数据量之间的关系，而空间复杂度则描述了算法执行过程中存储空间的需求。递归算法的空间复杂度通常比迭代算法高，因为它需要额外的栈空间来保存递归调用的上下文。

### 2.3.2 递归调用栈的理解与应用

递归调用栈是理解递归算法复杂度的关键组件，它记录了函数调用的层次和状态。每次函数调用都会在调用栈上添加一个新的帧，包含函数的局部变量和返回地址。理解递归调用栈对于分析递归算法的内存使用和潜在的栈溢出错误至关重要。

# 演示递归调用栈的Python代码示例
def recursive_trace(n):
    if n > 0:
        print(f"recursive_trace({n-1})")
        recursive_trace(n-1)
        print(f"recursive_trace({n}) end")

recursive_trace(3)

在上述代码中，每次递归调用 `recursive_trace` 时，都会打印当前调用的细节，并在调用栈的末尾添加一个新的帧。该示例清晰地展示了递归调用栈的工作原理及其在递归算法中的应用。

# 3. 递归在数据结构中的应用

## 3.1 树与图的递归遍历

### 3.1.1 二叉树的递归遍历算法

二叉树的递归遍历算法是一种典型的递归应用，它包括前序遍历、中序遍历和后序遍历。在遍历过程中，递归函数会首先处理当前节点的数据，然后递归地遍历左子树和右子树。

在前序遍历中，递归函数会首先输出当前节点的值，接着遍历左子树，最后遍历右子树。中序遍历则先遍历左子树，然后输出当前节点的值，最后遍历右子树。后序遍历的顺序则是先遍历左子树，接着遍历右子树，最后输出当前节点的值。

class TreeNode:
    def __init__(self, value):
        self.val = value
        self.left = None
        self.right = None

def preorder_traversal(root):
    if root is None:
        return []
    return [root.val] + preorder_traversal(root.left) + preorder_traversal(root.right)

# 递归遍历逻辑分析
# 这个函数首先检查当前节点是否为空，如果是，则返回一个空列表。
# 如果当前节点不为空，那么它会先将当前节点的值添加到结果列表中，
# 然后递归地调用preorder_traversal遍历左子树，将其结果添加到列表中，
# 最后递归地调用preorder_traversal遍历右子树，再次将其结果添加到列表中。

在上述代码中，我们定义了一个简单的二叉树节点类TreeNode，并实现了一个前序遍历的递归函数preorder_traversal。通过递归调用，我们能够遍历整个二叉树并按照前序遍历的顺序输出节点的值。

### 3.1.2 图的深度优先搜索（DFS）

深度优先搜索（DFS）是一种用于遍历或搜索树或图的算法。该算法沿着树的深度遍历树的节点，尽可能深地搜索树的分支。当节点v的所有邻接节点都已被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这个过程一直进行到已发现从源节点可达的所有节点为止。

def dfs(graph, start, visited=None):
    if visited is None:
        visited = set()
    visited.add(start)
    print(start)
    for next in graph[start] - visited:
        dfs(graph, next, visited)
    return visited

# 深度优先搜索逻辑分析
# 此函数接收三个参数：graph表示图结构，start表示起始节点，visited记录已经访问过的节点。
# 如果visited未指定，则初始化为一个空集合。
# 函数首先将start节点添加到visited集合中，表示已经访问过该节点。
# 然后对start节点的所有邻接节点进行遍历，
# 如果邻接节点不在visited集合中，则递归调用dfs函数继续访问。

在上述代码中，我们定义了一个简单的图结构，并实现了一个深度优先搜索的函数dfs。函数使用一个集合visited来记录已经访问过的节点，以避免重复访问。通过对每个节点的所有邻接节点进行递归搜索，我们可以实现图的深度优先遍历。

## 3.2 排序与搜索算法中的递归

### 3.2.1 快速排序与归并排序的递归实现

快速排序和归并排序是两种经典的使用递归实现的排序算法。快速排序通过对选定的元素进行分区操作，使得比它小的元素排在左边，