【递归算法设计模式】：构建灵活且可重用的递归解决方案

# 1. 递归算法的理论基础

递归算法是计算机科学中一个非常重要的概念，它通过让一个函数调用自身来解决问题。这种技术在解决涉及重复子问题的问题时尤为有用，比如在处理树形数据结构和图算法中。理解递归算法的理论基础是掌握其应用的关键第一步。

## 1.1 递归算法的基础概念

递归算法可以看作是数学归纳法的程序实现。基本思想是一个大问题可以通过分解为一个小问题的重复求解过程来解决。在这个过程中，最简单的情况（称为基准情况或递归终止条件）可以直接求解，而更复杂的情况则通过将大问题分解为小问题，并使用相同的算法来解决这些子问题。

## 1.2 递归算法的运行机制

递归算法的工作原理是基于调用栈，每次函数调用自身时，都会在调用栈上添加一个新的层级，其中存储了参数、局部变量和返回地址。当达到基准情况时，递归开始逐层返回，逐步执行返回地址上指令的过程，最终得到最终结果。理解调用栈的工作机制对于深入掌握递归算法至关重要。

递归算法的理论基础奠定了其在计算领域的广泛应用，不仅是数据结构和算法教学的核心内容之一，也是很多实际应用的基础。通过本章的介绍，我们对递归算法有了一个初步的理解，为后续章节的深入学习打下了基础。

# 2. 递归算法的核心原理

递归算法是计算机科学中一种非常重要的算法设计思想，其核心在于将复杂问题分解为规模较小的相似问题。递归算法的设计和分析，不仅对于理解算法本身至关重要，而且对于掌握程序设计的技巧和优化算法性能都具有重要的指导意义。

## 2.1 递归算法的定义和特性

### 2.1.1 递归算法的概念

递归算法可以被定义为一种能够直接或间接调用自身的算法。在递归算法中，一个问题的解决方法被应用于规模更小的相同问题，直到达到一个不再需要递归的简单情况，也就是基准情况（Base Case）。这种算法设计模式常用于解决可以分解为多个子问题的问题。

理解递归算法的关键在于识别问题的递归结构，这通常与问题的自然层次结构有关，如树形结构或图结构。递归算法可以大大简化代码的复杂性，因为递归调用会自动处理问题的分解和子问题结果的组合。

### 2.1.2 递归算法的运行机制

递归算法的运行机制可以分为两个阶段：递归阶段和回溯阶段。

在递归阶段，递归函数被调用以解决一个子问题，如果这个问题足够小以至于可以直接解决，那么函数将直接返回结果；如果还不够小，那么函数将调用自身来解决一个更小的子问题。这个过程会不断重复，直至问题缩减到基准情况。

在回溯阶段，函数开始逐层返回，每层返回都结合了当前问题的解与下层子问题的解。递归函数的执行栈会保留每一次调用的信息，包括局部变量和返回地址，直到所有递归调用都返回并解决顶层问题。

递归算法的运行机制图示可以使用mermaid流程图来描述：

graph TD
    A[开始递归算法] --> B{基准情况检查}
    B -- 是 --> C[返回基准情况结果]
    B -- 否 --> D[递归调用]
    D --> B
    C --> E[回溯阶段]
    E --> F[结合子问题解]
    F --> G[继续递归或返回最终结果]

## 2.2 递归算法的设计模式

### 2.2.1 分而治之模式

分而治之（Divide and Conquer）是一种递归策略，将原问题分解为若干个规模较小但类似于原问题的子问题，递归地解决这些子问题，然后再合并这些子问题的解以产生原问题的解。

举个例子，快速排序算法就运用了分而治之的模式。它将数组分为两个子数组，分别递归地排序这两个子数组，然后合并排序结果。

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quick_sort(left) + middle + quick_sort(right)

# 示例数组
print(quick_sort([3,6,8,10,1,2,1]))

### 2.2.2 动态规划模式

动态规划（Dynamic Programming）是一种优化递归算法的方法，通过存储已经计算过的子问题的解，避免重复计算，从而提高效率。动态规划通常用于求解最优化问题。

例如，经典的斐波那契数列问题，通过动态规划可以将时间复杂度从指数级优化到线性级。

def fibonacci(n):
    if n == 0: return 0
    elif n == 1: return 1
    else:
        fib = [0] * (n+1)
        fib[1] = 1
        for i in range(2, n+1):
            fib[i] = fib[i-1] + fib[i-2]
        return fib[n]

# 计算第10个斐波那契数
print(fibonacci(10))

### 2.2.3 回溯模式

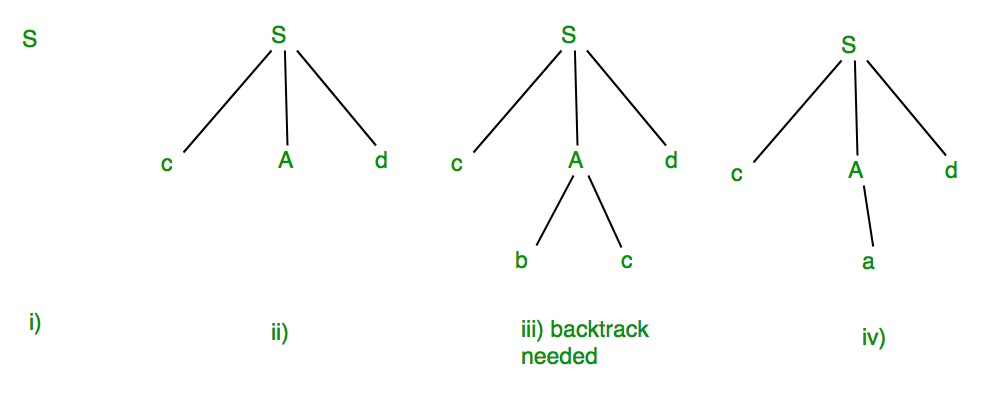
回溯（Backtracking）算法是一种通过试错来寻找所有解的算法。它通过递归来遍历所有可能的候选解，如果候选解被确认不是一个有效的解（或者至少不是最后一个解），则回溯并放弃上一步或者当前步骤作出的选择，尝试其他可能的选择。

一个典型的回溯算法应用是八皇后问题，目标是在8×8的棋盘上放置八个皇后，使得它们互不攻击。

def is_safe(board, row, col):
    # 检查在当前位置放置皇后是否安全
    pass # 此处省略具体实现细节

def solve_n_queens(board, col):
    if col >= len(board):
        return True # 所有皇后都已经放置成功
    for i in range(len(board)):
        if is_safe(board, i, col):
            board[i][col] = 'Q'
            if solve_n_queens(board, col + 1):
                return True
            board[i][col] = '.' # 回溯
    return False

# 初始化棋盘，使用长度为8的列表，每个位置用'.'表示空，'Q'表示皇后
board = [['.' for _ in range(8)] for _ in range(8)]
if solve_n_queens(board, 0):
    # 如果找到解决方案，则打印棋盘
    for row in board:
        print(' '.join(row))
else:
    print("No solution found")

## 2.3 递归算法的效率分析

### 2.3.1 时间复杂度分析

递归算法的时间复杂度分析是确定算法执行时间随着输入规模增长的趋势。递归算法的时间复杂度往往与递归的深度以及每个递归层级上的操作数有关。

例如，对于分而治之模式的快速排序，最好情况下的时间复杂度是O(n log n)，但在最坏情况下（如输入数组已经是排序好的），时间复杂度会退化到O(n²)。

### 2.3.2 空间复杂度分析

空间复杂度是指算法在运行过程中临时占用存储空间的大小。对于递归算法而言，空间复杂度主要取决于递归调用的深度，即栈的大小。

在上述动态规划的斐波那契数列实现中，空间复杂度是O(n)，因为只存储了n个数的数组。而对于快速排序，空间复杂度最差情况下是O(n)，因为递归调用可能会很深。

在第二章中，我们详细探讨了递归算法的定义、设计模式和效率分析。在接下来的章节中，我们将深入实践应用，并分享更多关于递归算法在不同领域中的应用案例。

# 3. 递归算法的实践应用

## 3.1 数据结构中的递归应用

### 3.1.1 树的遍历算法

在计算机科学中，树是一种重要的非线性数据结构，它模拟了具有层次关系的组织结构。树的遍历算法是递归算法应用的一个典型例子，其中最常见的遍历方式有前序遍历、中序遍历和后序遍历。

前序遍历是一种递归遍历树的方式，按照“根-左-右”的顺序访问每个节点。以下是前序遍历算法的递归实现示例：

def preorder_traversal(node):
    if node is None:
        return
    # 处理当前节点（例如打印节点值）
    process(node.value)
    # 递归遍历左子树
    preorder_traversal(node.left)
    # 递归遍历右子树
    preorder_traversal(node.right)

逻辑分析与参数说明：
- `preorder_traversal`函数接受一个节点`node`作为参数。
- 如果当前节点`node`为空，表示已到达树的底部，递归终止。
- 对当前节点进行处理，通常是对节点值进行某些操