【数据结构对比分析】：哈希表与其他数据结构的性能战争，谁是王者？

# 1. 数据结构的基本概念与分类

在计算机科学中，数据结构是组织和存储数据的一种方式，它使得我们可以有效地访问和修改数据。数据结构的种类繁多，但它们大体上可以分为线性结构和非线性结构两大类。线性结构像数组和链表，它们的数据元素之间存在一对一的关系；而非线性结构如树和图，它们的数据元素之间存在着一对多或多对多的关系。

理解数据结构的基础是理解它们如何被用来表示信息。数据类型决定了数据结构中的元素类型，以及可以对这些元素执行的操作。数据结构的分类依据其逻辑结构（数据元素间的关系）和物理存储结构（数据在计算机中的存储方式）。

在深入学习数据结构之前，我们需要了解它的基本概念，包括抽象数据类型（ADT）、数据的逻辑结构、物理存储结构，以及操作数据的方法。这些基础概念为我们学习更复杂的算法和数据结构打下了坚实的基础。下面章节将继续深入探讨具体的数据结构类型及其应用。

# 2. 哈希表的工作原理与应用场景

## 2.1 哈希表的内部结构与操作

### 2.1.1 哈希函数的设计原则

哈希函数是哈希表的灵魂，它负责将数据映射到一个确定的索引位置。设计良好的哈希函数应遵循几个关键原则：

- **唯一性**：尽可能减少不同输入数据映射到同一索引位置的情况（即冲突）。
- **一致性**：相同的数据输入应该总是产生相同的索引输出。
- **效率**：哈希函数的计算过程要足够快，以确保哈希表的效率不被哈希函数的计算拖累。
- **均匀分布**：数据应该均匀地分布在哈希表中，以避免某些区域的过载而其他区域空闲。

下面是一个简单的哈希函数例子，使用Java语言编写，它将字符串映射到哈希表索引：

public int hashFunction(String key) {
    int hashValue = 0;
    for (int i = 0; i < key.length(); i++) {
        hashValue = (hashValue * 31 + key.charAt(i)) % tableSize;
    }
    return hashValue;
}

这里的`tableSize`是哈希表的大小，`31`是一个质数，选择质数作为乘数可以提高哈希值的唯一性。乘法后模`tableSize`确保结果索引值在哈希表范围内。

### 2.1.2 冲突解决机制详解

尽管哈希函数努力达到均匀分布，但冲突仍然是不可避免的。为了应对冲突，哈希表采用了多种解决机制：

- **开放寻址法**：当发现冲突时，线性探测下一个空位置，或者根据某种规则找到一个新的空槽位。
- **链地址法**：将所有具有相同哈希值的数据项存储在一个链表中。
- **再哈希法**：使用另一个哈希函数计算新的索引。

在链地址法中，每个槽位不仅存储一个数据项，还存储一个链表的引用。当冲突发生时，新数据项会被添加到对应槽位的链表中。

class HashTable {
    private LinkedList>[] table;
    private int tableSize;

    public HashTable(int size) {
        table = new LinkedList[size];
        tableSize = size;
    }

    public void insert(String key) {
        int index = hashFunction(key) % tableSize;
        if (table[index] == null) {
            table[index] = new LinkedList<>();
        }
        table[index].add(key);
    }
}

在这个简单的哈希表实现中，每个槽位是一个链表。插入操作将新键添加到对应索引的链表末尾。

## 2.2 哈希表的性能分析

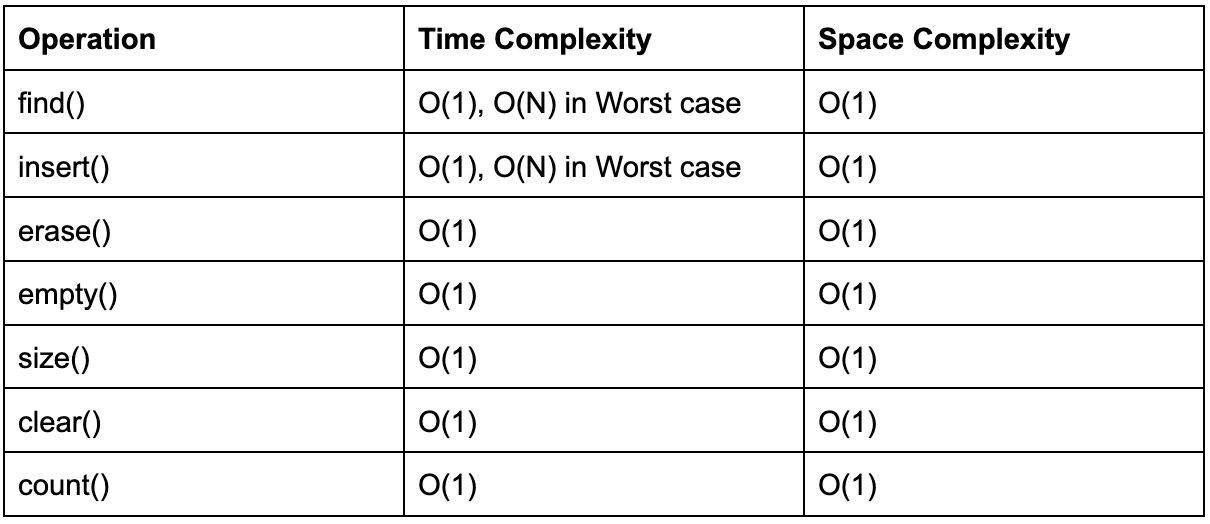
### 2.2.1 时间复杂度与空间复杂度

哈希表的核心优势在于其近似O(1)的平均时间复杂度，这意味着查找、插入和删除操作都大约在常数时间内完成。这是在理想情况下，即哈希函数分布均匀且哈希表未达到过载状态时的情况。

然而，当哈希冲突频繁发生时，性能将退化到O(n)，尤其是使用链地址法且链表过长时。因此，哈希表的时间复杂度可以表述为：

- **平均时间复杂度**：O(1)
- **最坏情况时间复杂度**：O(n)

空间复杂度相对简单，哈希表的空间被用于存储数据项和链表（如果是链地址法），因此其空间复杂度为O(n)，其中n是数据项的数量。

### 2.2.2 平均与最坏情况性能对比

为了更深入地理解哈希表的性能，让我们构建一个哈希表，并对平均和最坏情况性能进行比较：

- **平均情况**：假设哈希表的负载因子（即数据项与哈希表大小的比例）相对较低，大部分数据项被成功地分配到不同的槽位中。此时，大部分操作都可以在常数时间内完成。
- **最坏情况**：当哈希表接近满载时，大量数据项可能会被分配到相同的槽位。此时，如果使用链地址法，每个槽位的链表将增长，所有操作可能退化到线性时间。

在性能测试中，可以通过逐步增加数据项的数量来观察性能变化：

public static void main(String[] args) {
    int size = 100; // 哈希表大小
    HashTable hashTable = new HashTable(size);
    List<String> keys = ... // 数据项集合

    // 插入数据项并测量时间
    long startTime = System.nanoTime();
    for (String key : keys) {
        hashTable.insert(key);
    }
    long endTime = System.nanoTime();
    // 输出平均和最坏情况下的性能数据
    ...
}

## 2.3 哈希表的实际应用案例

### 2.3.1 高效查找场景的解决方案

哈希表在需要快速查找的场景下表现得尤为出色。一个典型的例子是搜索引擎中的关键词索引。搜索引擎使用哈希表来快速找到对应的关键字及其相关链接。

### 2.3.2 哈希表在缓存系统中的角色

缓存系统广泛使用哈希表作为其内部数据结构，以实现快速的查找、插入和删除操作。例如，网页浏览器缓存使用哈希表来存储最近访问的网页内容，以便用户能够快速地重新加载页面。

以上内容构成了本文的第二章内容，详细介绍了哈希表的工作原理、性能分析以及实际应用场景。接下来的章节将探讨哈希表与数组、链表等数据结构的性能对比，以及更高级数据结构的较量。

# 3. 哈希表与数组、链表的性能对比

## 3.1 数组与哈希表的效率对比

### 3.1.1 访问速度的直接比较

数组和哈希表在访问速度上有着本质的区别。数组的访问速度非常快，因为它是一种连续的内存空间，可以通过索引直接访问元素。由于内存的连续性，处理器可以利用预取（prefetching）机制提前加载内存中的数据到缓存中，使得数组访问接近CPU处理速度的上限。

哈希表则是通过键（Key）来间接访问值（Value），需要一个哈希函数将键转换为数组索引。在理想情况下，哈希函数能够均匀分布键到数组索引，从而实现快速访问。然而，哈希冲突的存在可能会降低访问速度，因为冲突需要额外的操作来解决。

# Python数组访问示例
arra