【性能下降快速诊断】：哈希表性能危机，专家教你如何应对

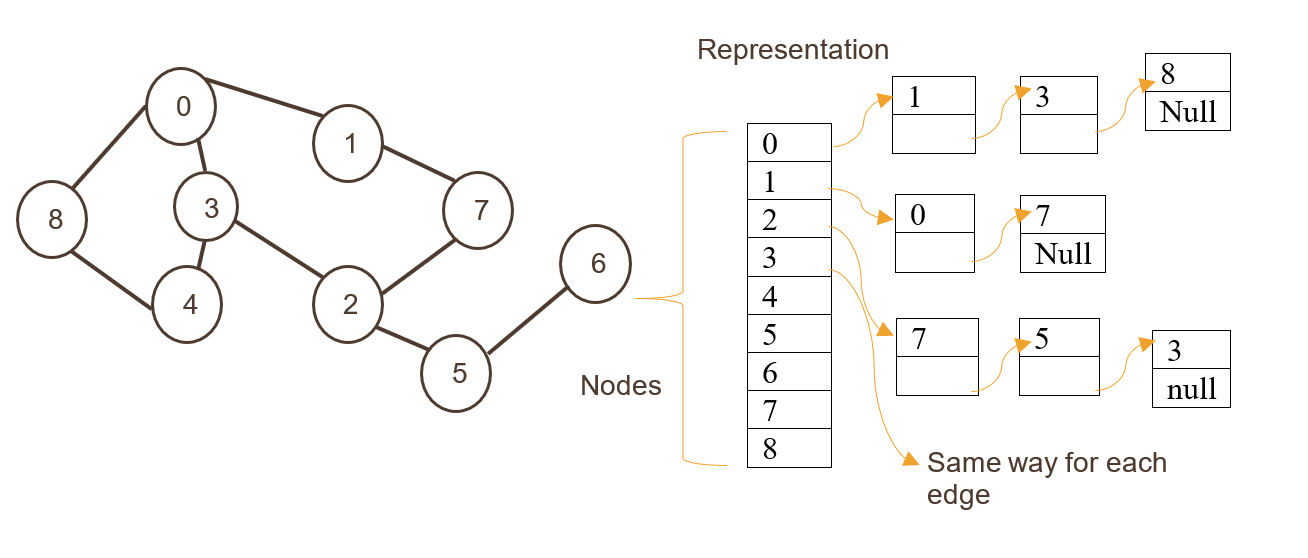
# 1. 哈希表性能危机概述

在现代计算机科学和信息技术领域，数据管理是构建高效系统的关键。哈希表作为一种广泛使用的数据结构，以其快速的查找性能著称。然而，在高负载和复杂的应用场景下，哈希表的性能危机逐渐显现，导致数据处理效率降低，系统响应速度缓慢。本章将概述哈希表性能危机的表现形式、背后成因以及带来的挑战。

## 1.1 性能危机的表现

哈希表性能危机主要表现在两个方面：查询速度显著下降和内存使用率异常。当哈希表中的键值对数量大幅增加，碰撞率上升时，原本常数时间复杂度的查找操作会退化成线性时间复杂度，效率急剧下降。

## 1.2 引发危机的原因

哈希表性能危机的根本原因在于其设计结构和应用环境。当哈希表的负载因子（即已填充槽位的比例）过高，或者哈希函数设计不合理导致碰撞无法有效处理时，性能问题就会暴露出来。

## 1.3 应对策略的重要性

面对性能危机，采取有效的应对策略至关重要。例如，定期进行哈希表的容量扩展和优化哈希函数设计，可以预防和缓解性能下降的问题，保持系统的高效运转。后续章节将深入探讨性能优化的理论基础和实践方法。

# 2. 哈希表理论基础与性能分析

哈希表作为一种重要的数据结构，在计算机科学和软件工程中扮演着关键角色。其基本原理是通过哈希函数将键映射到存储桶（bucket）上，以便快速访问数据。然而，哈希表的性能并非一成不变，它受到多种因素的影响。本章将深入探讨哈希表的工作原理、性能影响因素以及常见性能问题案例。

## 2.1 哈希表的原理和实现

### 2.1.1 哈希函数的设计

哈希函数的设计是哈希表高效运行的基础。一个优秀的哈希函数需要满足两个基本条件：计算速度快以及尽可能减少键值冲突。常见的哈希函数有直接定址法、除留余数法、平方取中法等。

代码块展示一个简单的除留余数法哈希函数实现（Python示例）：

def simple_hash(key, table_size):
    """
    哈希函数实现示例
    :param key: 输入的键
    :param table_size: 哈希表的大小
    :return: 计算得到的哈希值
    """
    return key % table_size

上述代码中，我们使用模运算来计算哈希值。这种方式简单快速，但是要注意避免模运算的同余风险，例如当`table_size`是2的幂时，所有的奇数键将会映射到奇数索引位置，造成偶数索引位置的浪费。

### 2.1.2 冲突解决机制

当两个键通过哈希函数计算得到相同的哈希值时，即发生了冲突。解决冲突的常见机制有开放寻址法和链表法。

开放寻址法中，当发现一个位置已被占用时，会在哈希表中按照某种规则寻找下一个空位置。而链表法则是在每个哈希桶中使用链表来存储所有键值对。代码实现如下（链表法实现的简单哈希表）：

class HashTable:
    def __init__(self, size):
        self.size = size
        self.table = [[] for _ in range(size)]

    def hash_function(self, key):
        return key % self.size

    def insert(self, key, value):
        key_hash = self.hash_function(key)
        for i, (k, v) in enumerate(self.table[key_hash]):
            if k == key:
                self.table[key_hash][i] = (key, value)
                return
        self.table[key_hash].append((key, value))

    def search(self, key):
        key_hash = self.hash_function(key)
        for k, v in self.table[key_hash]:
            if k == key:
                return v
        return None

## 2.2 哈希表性能的影响因素

### 2.2.1 负载因子与性能关系

负载因子（load factor）是衡量哈希表性能的指标之一，定义为已存储的元素数量除以哈希表的总容量。负载因子的大小直接影响哈希表的性能，包括搜索、插入和删除操作的效率。当负载因子过高时，冲突可能性增大，性能下降。因此，适时调整哈希表的大小是必要的。

### 2.2.2 动态扩展的必要性

随着元素数量的增加，哈希表需要动态扩展以维持性能。动态扩展意味着增加哈希表的容量并重新分配现有元素。通常情况下，当负载因子达到某个阈值时，哈希表就需要进行动态扩展。这通常涉及到创建一个更大的哈希表，并将旧表中的元素重新插入到新表中。

## 2.3 常见性能问题案例分析

### 2.3.1 慢查询的诊断方法

在哈希表中，慢查询通常是由于高冲突率导致的。诊断慢查询的常见方法包括监控哈希表的负载因子、记录插入/搜索/删除操作的性能指标以及使用性能分析工具。通过这些方法，我们可以确定是否需要调整哈希表大小或者优化哈希函数。

### 2.3.2 数据倾斜现象的识别与应对

数据倾斜是指在分布式哈希表中，某些节点上的数据量远大于其他节点的现象。这种不均衡的数据分布会导致性能瓶颈。识别数据倾斜通常需要监控各个节点的负载情况，解决策略可能包括重新哈希算法和使用一致性哈希等技术来优化数据分布。

## 章节小结

在本章中，我们对哈希表的工作原理进行了深入分析，并探讨了影响其性能的关键因素，例如哈希函数的设计、负载因子以及动态扩展的必要性。通过对慢查询的诊断方法和数据倾斜现象的识别，我们认识到在实际应用中，调整和优化哈希表结构的重要性。本章的内容为下一章关于哈希表性能优化的实践策略提供了理论基础。

# 3. 哈希表性能优化的实践策略

## 3.1 数据结构的调整与优化

### 3.1.1 选择合适的哈希表结构

在选择合适的哈希表结构时，需要根据应用场景的具体需求来进行。常见的哈希表实现包括链表法（Separate Chaining）和开放寻址法（Open Addressing），每种方法都有其优缺点。

- 链表法通过在每个哈希槽中维护一个链表来解决冲突，适用于元素数量动态变化的场景。它在表中元素较多时能够很好地处理冲突，但会带来额外的空间开销，并且在遍历数据时可能需要多次内存访问。

- 开放寻址法则是尝试在哈希表的其他位置查找空位来存储冲突的数据。这种方法可以减少空间开销，但是当负载因子较高时，性能会急剧下降，尤其是在进行删除操作时可能会引发“二次聚集”问题。

根据数据访问模式和性能要求选择最合适的哈希表结构至关重要。在实际应用中，我们可以使用如下的评估标准：

- 当哈希表中的元素数量变化不大且负载因子较低时，可以优先考虑使用开放寻址法。
- 对于元素数量动态变化的场景，特别是需要频繁插入和删除的场景，链表法则更为合适。
- 对于内存使用非常敏感的应用，可以考虑使用带有尾部删除优化的链表法，以减少内存碎片。

### 3.1.2 内存使用优化技巧

内存的优化直接关系到哈希表的性能，尤其是在处理大数据量时。以下是一些内存优化技巧：

- **内存池技术**：通过预先分配一大块内存作为内存池，可以减少动态内存分配时的开销，并且可以更有效地利用内存碎片。
- **对象复用**：在哈希表内部维护对象池，对于频繁增删的数据，复用已经存在的对象，避免频繁创建和销毁对象。
- **内存对齐**：合理安排内存布局，利用现代CPU的缓存和预读机制，减少内存访问的延迟。

例如，在C++中，使用`std::unordered_map`时，可以通过自定义哈希函数和分配器来达到内存优化的目的：

#include <unordered_map>
#include <memory>

// 自定义分配器
template <typename T>
struct MyAllocator {
  using value_type = T;
  MyAllocator() = default;
  template <class U>
  MyAllocator(const MyAllocator<U>&) {}
  T* allocate(size_t n) {
    // 使用内存池分配
    return static_cast<T*>(pooled_memory_alloc(n));