【性能参数微调】：哈希表调优实战，提升性能的参数调整技巧

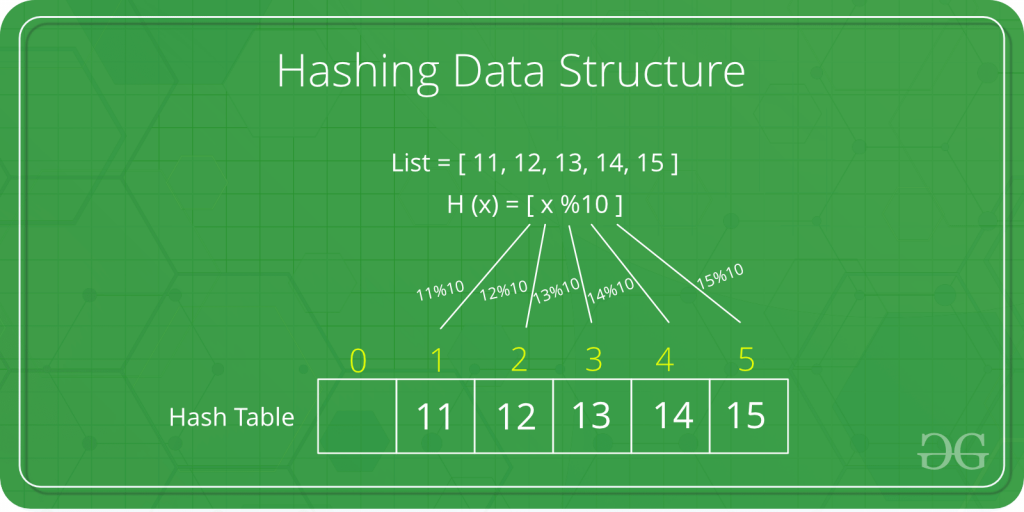
# 1. 哈希表与性能微调概述

在现代IT领域中，数据的存储与检索效率至关重要，而哈希表作为一种常用的数据结构，在许多应用中扮演着核心角色。本章旨在为读者提供哈希表及其性能微调的初步认识，揭示其在性能优化中的重要作用。

## 1.1 哈希表的基本原理与应用

哈希表通过一个哈希函数将键（key）映射到存储位置（槽位），使得插入、删除和查找操作的平均时间复杂度达到O(1)，极大地提升了数据处理速度。在诸如数据库索引、缓存系统、搜索引擎等领域，哈希表被广泛应用，其性能直接影响着整个系统的响应速度和稳定性。

## 1.2 性能微调的重要性

然而，哈希表并非没有局限。其性能会受到负载因子、冲突解决机制等因素的影响。对哈希表的性能进行微调，意味着在保持高效检索的同时，也要保证系统的整体性能。本章将为读者呈现对哈希表性能微调的概述，为后续章节深入分析奠定基础。

# 2. 哈希表基础理论

## 2.1 哈希表的数据结构解析
### 2.1.1 哈希表的基本概念

哈希表是一种基于键值对(key-value pair)的数据结构，允许使用一个值（键）来高效查找另一个值（值）。它通过哈希函数将键映射到表中的位置（或称为槽slot），从而可以快速地访问数据项，而不必遍历整个数据集合。哈希表的基本特点在于它提供了接近常数时间的查找性能，通常表示为O(1)，当然这是在理想情况下，实际中可能由于哈希冲突等原因导致性能有所下降。

哈希表的关键组成部分包括：

- 哈希函数（Hash Function）：将键转换为表中的索引。
- 数组（或称为桶bucket）：用于存储数据项的线性数据结构。
- 键（Key）：用于定位表中数据项的标识符。
- 值（Value）：与键相关联的数据。

在设计哈希表时，哈希函数的品质至关重要，它决定了数据项在表中的分布情况。一个好的哈希函数会尽可能地减少冲突，使得数据均匀分布在整个数组中。

### 2.1.2 哈希函数的分类和原理

哈希函数按其设计原理大致可以分为以下几类：

- 直接定址法：直接使用键的一部分或全部作为索引。这种方法简单但冲突多，适用性较差。
- 除留余数法：键值被除以一个数，然后取余数作为索引。选择一个合适的质数作为除数能够较好地减少冲突。
- 数字分析法：利用键的位数或数字特性来设计哈希函数，适用于键的数字分布有特点时。
- 平方取中法：取键值平方后的中间几位作为索引，这种方法适用于键的位数不长也不短的情况。
- 随机映射法：使用随机数作为哈希函数，这使得索引的位置难以预测，可以在某些特殊情况下使用。

哈希函数在设计时需要考虑的关键因素包括：

- 快速计算：哈希函数应当容易且快速计算。
- 高效分布：哈希值应均匀分布以减少冲突。
- 安全性：在需要安全性的应用中，哈希函数需要足够抵抗各种攻击。

## 2.2 哈希表的性能评估指标
### 2.2.1 时间复杂度和空间复杂度

哈希表的性能通常通过时间复杂度和空间复杂度来评估。在不考虑冲突的情况下，哈希表的时间复杂度为O(1)，意味着无论表的大小如何，查找、插入或删除操作的平均时间保持不变。然而，在现实中，冲突总是存在，因此时间复杂度可能会上升到O(n)，在极端情况下，当所有元素都发生冲突时，时间复杂度接近链表的性能O(n)。

空间复杂度方面，哈希表通常需要预留出比实际存储的键值对数量还要多的空间来减少冲突。理想情况下，空间复杂度为O(n)，但是考虑到额外的存储空间用于解决冲突，实际的空间复杂度可能会更高。

### 2.2.2 冲突解决机制的影响

冲突是哈希表中不可避免的问题，冲突解决机制的效率直接影响哈希表的性能。常见的冲突解决机制包括：

- 开放定址法：当发生冲突时，通过某种方法在表内重新查找一个空闲位置。
- 链表法：每个索引位置维护一个链表，将所有冲突的元素以链表的形式存储。

这些冲突解决机制对性能的影响如下：

- 开放定址法对于小数据集或较低的加载因子较为高效，但是随着数据量的增加，性能会急剧下降。
- 链表法通常具有更高的空间开销，因为每个索引位置都要存储一个链表，但其优点是扩展性好，并且对于删除操作更加高效。

在设计哈希表时，需要权衡性能与空间效率，选择最适合应用场景的冲突解决机制。

flowchart LR
    A[哈希表] -->|查找| B[哈希函数]
    B -->|计算索引| C[数组]
    C -->|访问数据| D[键值对]
    E[冲突解决] --> F[开放定址法]
    E --> G[链表法]
    F -->|插入| C
    G -->|插入| H[链表]
    H -->|遍历| C

在上述流程图中，我们看到了哈希表在查找操作中，哈希函数计算得到的索引直接指向数组中的位置。如果发生冲突，则根据选择的冲突解决策略，如开放定址法或链表法，来决定接下来的步骤。开放定址法需要在数组内寻找新的空闲位置，而链表法则需要遍历链表找到合适的位置。

| 指标 | 开放定址法 | 链表法 |
| --- | --- | --- |
| 时间复杂度 | 最坏O(n) | 最好O(1) |
| 空间复杂度 | O(n) | O(n+k)，k为冲突元素数量 |
| 删除操作 | 复杂，可能需要移动元素 | 简单，仅删除链表节点 |
| 实现复杂度 | 较低 | 较高 |

如上表所示，对比开放定址法和链表法的性能和实现复杂度。对于开放定址法，最坏情况下可能需要遍历整个数组来解决冲突，时间复杂度达到O(n)。链表法在理想情况下（即很少有冲突）能够达到O(1)的查找速度，但空间开销会增加。删除操作中，开放定址法可能需要对数组中的多个元素进行移动，而链表法仅需要操作链表节点，相对简单。

在选择冲突解决机制时，通常需要考虑数据集的大小、预期的加载因子、以及对删除操作的需求等因素。

# 3. 哈希表性能参数的理论分析

## 3.1 负载因子的理解与调整

### 3.1.1 负载因子对性能的影响

负载因子（Load Factor）是衡量哈希表中元素填充程度的一个重要指标，其定义为元素总数与表大小的比值。计算公式为：

负载因子 = 元素总数 / 表大小

负载因子对哈希表的性能有直接的影响：

- **存储效率**：较高的负载因子意味着表中的空间被更充分地利用，减少了内存的浪费。但是当负载因子过高时，表中元素过于拥挤，冲突的可能性增加，从而导致性能下降。
- **搜索效率**：当负载因子较低时，表中的冲突较少，搜索效率较高。但是，低负载因子意味着哈希表占用更多内存空间。
- **扩容影响**：负载因子的大小决定了何时进行哈希表的扩容操作。频繁的扩容会影响性能，因为它涉及重新哈希和数据迁移。

### 3.1.2 理论模型下的负载因子优化

在理想情况下，负载因子应当根据哈希表的使用场景和性能要求来决定。以下是一些优化负载因子的经验法则：

- **动态调整**：初始化一个合理的负载因子，并根据实际运行情况动态调整。当连续出现多次哈希冲突时，可以适时增加负载因子阈值来触发扩容。
- **基于冲突计数的调整**：可以维护一个冲突计数器，在每次哈希冲突时增加计数器的值。当冲突计数达到某个阈值时，进行负载因子的动态调整和表的扩容。

graph LR
    A[开始] --> B{检查冲突}
    B -->|无冲突| C[继续操作]