【Java数据结构与算法】：单向链表的8种排序方法精讲

# 1. Java单向链表的数据结构基础

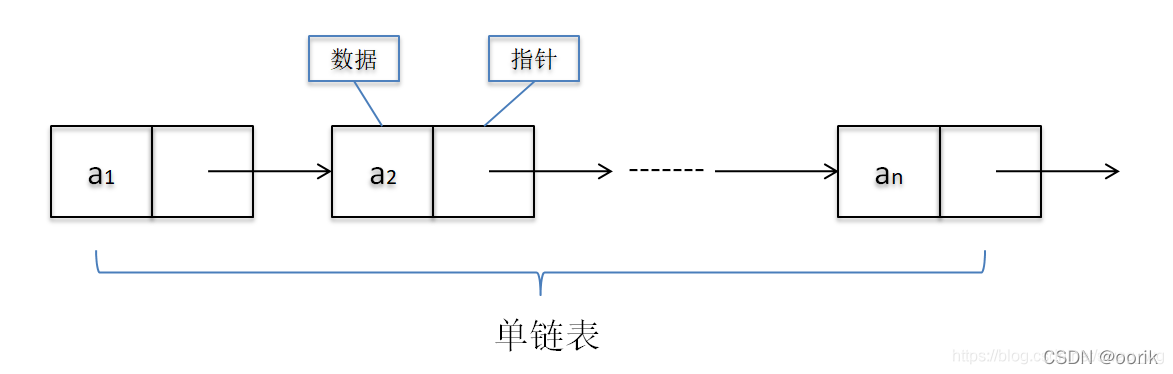
单向链表是一种常见的基础数据结构，它由一系列节点组成，每个节点包含数据部分和指向下一个节点的指针。在Java中，这通常通过创建一个含有两个属性的Node类来实现：一个用于存储数据的元素，另一个用于存储对下一个节点的引用。本章将介绍单向链表的基本概念，包括节点的创建、链表的添加、删除和遍历操作。我们将通过具体的Java代码示例来展示这些操作，从而帮助读者理解单向链表在内存中的动态结构以及节点间是如何相互连接的。

在进一步探讨链表的应用之前，我们首先需要明确单向链表的结构和特性。单向链表的特性在于它的“单向性”，即每个节点只知道下一个节点的位置，而不了解前一个节点的情况。这种结构使得在链表末尾添加和删除元素变得简单快捷，但在访问元素时需要从头节点开始遍历，直到找到目标节点。

下面是一个简单的Java单向链表节点类的实现代码：

class Node {
    int data; // 存储数据
    Node next; // 指向下一个节点的引用

    public Node(int data) {
        this.data = data;
        this.next = null;
    }
}

class LinkedList {
    Node head; // 链表头节点引用

    public LinkedList() {
        this.head = null;
    }

    // 添加节点到链表末尾
    public void add(int data) {
        Node newNode = new Node(data);
        if (head == null) {
            head = newNode;
            return;
        }
        Node current = head;
        while (current.next != null) {
            current = current.next;
        }
        current.next = newNode;
    }

    // 打印链表所有节点
    public void printList() {
        Node current = head;
        while (current != null) {
            System.out.print(current.data + " -> ");
            current = current.next;
        }
        System.out.println("null");
    }
}

public class Main {
    public static void main(String[] args) {
        LinkedList list = new LinkedList();
        list.add(1);
        list.add(2);
        list.add(3);
        list.printList(); // 输出: 1 -> 2 -> 3 -> null
    }
}

在这个基础示例中，我们定义了一个`Node`类用于存储链表的每个节点数据，以及一个指向下一个节点的指针。`LinkedList`类则提供了操作链表的接口，包括添加元素和打印链表。通过这个基础结构，我们可以在后续章节中探索和实现各种链表排序算法。

# 2. 单向链表排序算法的理论基础

### 2.1 排序算法概述

排序算法是计算机程序设计中不可或缺的一部分，用于将元素按特定顺序排列。对于链表来说，由于其特殊的非连续内存存储特性，一些排序算法需要特别的考虑和实现方式。

#### 2.1.1 算法效率分析

在进行算法效率分析时，通常会考察两个主要因素：时间复杂度和空间复杂度。时间复杂度描述的是算法执行时间与输入数据大小之间的关系，而空间复杂度则衡量了算法需要额外存储空间的多少。

- 时间复杂度：通常用大O符号来表示，它描述的是最坏情况下算法执行所需时间的上界。
- 空间复杂度：它代表了执行算法过程中的内存消耗，包括临时变量以及递归调用栈。

对于单向链表的排序算法，其时间复杂度通常和链表的长度n有关，我们经常看到的有O(n^2)、O(nlogn)等表示形式。空间复杂度则与算法是否需要额外空间有关，例如原地排序算法的空间复杂度为O(1)，非原地排序则可能需要O(n)的空间。

#### 2.1.2 时间复杂度和空间复杂度

在选择排序算法时，时间复杂度和空间复杂度是两个重要的衡量指标。时间复杂度决定了算法的执行效率，而空间复杂度则决定了算法的资源占用。

- 对于时间复杂度，O(1)最优，即算法的时间消耗不随输入数据规模增加而增加。
- 对于空间复杂度，O(1)同样是最优的，表示算法在执行过程中几乎不消耗额外空间。

接下来的章节将深入探讨单向链表排序算法中的冒泡排序与插入排序，理解其原理并以Java语言实现。这些算法在时间复杂度和空间复杂度上表现出不同的特点，能够帮助我们更好地理解和选择适合链表数据结构的排序算法。

# 3. 单向链表的冒泡排序与插入排序

## 3.1 冒泡排序的原理与实现
### 3.1.1 冒泡排序基本概念
冒泡排序算法是一种简单的排序算法，它重复地遍历要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。遍历数列的工作是重复进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

冒泡排序是稳定排序算法，即相等的元素在排序前后的相对顺序不变。尽管冒泡排序是一种简单直观的排序方法，但其效率较低，在处理大量数据时效率不是很高，特别是对于部分已经有序的序列。对于链表这种数据结构，由于缺乏随机访问的能力，冒泡排序在链表上的实现会有所不同，但原理不变。

### 3.1.2 单向链表冒泡排序的Java实现
在单向链表上进行冒泡排序时，需要遍历链表，通过节点间的指针进行元素的交换。由于不能像数组那样直接通过索引访问元素，我们需要采用迭代的方式，逐个访问链表节点，并进行比较和交换。

以下是Java实现单向链表冒泡排序的一个例子：

class ListNode {
    int val;
    ListNode next;

    ListNode(int x) {
        val = x;
        next = null;
    }
}

public class LinkedListSort {
    public static ListNode bubbleSortLinkedList(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }
        boolean swapped;
        ListNode dummy = new ListNode(0);
        dummy.next = head;
        do {
            swapped = false;
            ListNode current = dummy;
            ListNode prev = null;
            while (current.next != null && current.next.next != null) {
                if (current.next.val > current.next.next.val) {
                    // Perform swap
                    int temp = current.next.val;
                    current.next.val = current.next.next.val;
                    current.next.next.val = temp;
                    swapped = true;
                }
                prev = current;
                current = current.next;
            }
        } while (swapped);
        return dummy.next;
    }
}

该段代码首先判断链表是否为空或只包含一个节点，若是则直接返回。否则，通过一个循环进行多轮冒泡，每轮冒泡都从头节点开