模型评估指标全解析：如何选择最佳模型并优化性能

# 1. 模型评估指标概论

在机器学习与数据挖掘领域，模型评估是确保构建的模型有效、可靠并具备广泛适用性的关键环节。评估指标不仅用于衡量模型的性能，还可以指导我们对模型进行优化。本章将探讨评估指标的基础概念、在分类与回归问题中的不同应用以及多类别分类问题的特殊考量，为后续章节提供理论基础。

## 1.1 评估指标的作用与重要性

评估指标帮助我们回答"模型表现如何？"这一核心问题。在不同的问题类型中，我们关注的指标也有所不同。例如，在分类问题中，我们可能关注模型预测的准确性，而在回归问题中，我们可能更关心预测值与实际值的偏差大小。正确选择并应用评估指标，能够为模型选择提供客观的依据，确保模型在未见数据上也能有良好的表现。

## 1.2 常用评估指标简介

常用的模型评估指标包括：

- 分类问题：准确度、精确率、召回率、F1分数、ROC曲线与AUC值。
- 回归问题：均方误差（MSE）、均方根误差（RMSE）、决定系数（R²）、平均绝对误差（MAE）。
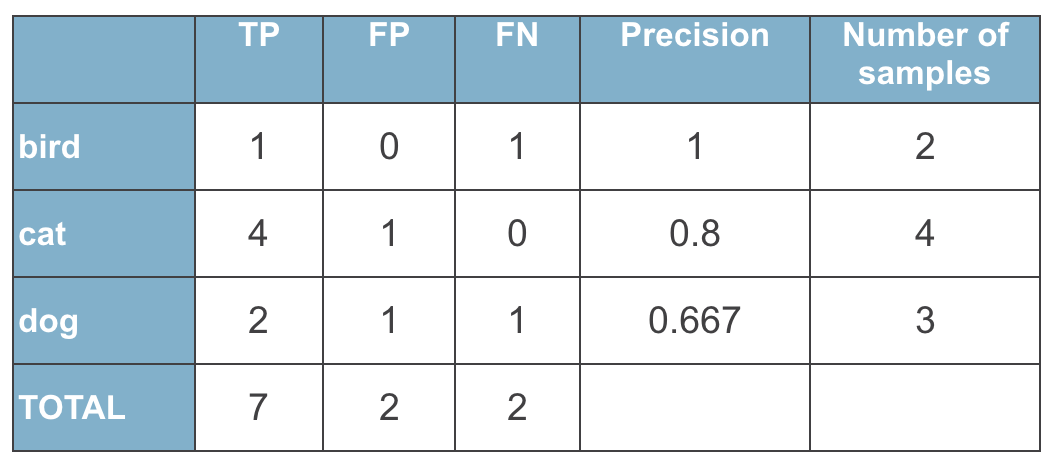
- 多类别分类：混淆矩阵、宏平均、微平均和交叉验证。

在接下来的章节中，我们将详细探讨这些指标的定义、计算方法以及应用场景。通过这些内容的学习，读者将能够更好地掌握模型评估的技巧，并在实践中做出更明智的选择。

# 2. 分类问题的评估指标

### 2.1 准确度与精确率

#### 2.1.1 准确度的定义及计算方式
在分类任务中，准确度（Accuracy）是最直观的评估指标，它表示分类正确的样本数占总样本数的比例。准确度的计算公式如下：

\[ \text{Accuracy} = \frac{\text{正确预测的样本数量}}{\text{总样本数量}} \]

尽管准确度易于理解和计算，但在数据不平衡的情况下，它可能不是最好的评估指标。例如，如果一个数据集中99%的样本属于某一类，那么一个始终预测该类别的简单模型也可以获得很高的准确度，但实际上该模型并未有效地学习到其他类别的特征。

准确度的计算过程通常涉及到混淆矩阵，它是评价分类质量的一个重要工具。在混淆矩阵中，每一行代表实际类别，每一列代表预测类别。准确度是所有正确预测的样本数（即对角线上的元素）除以总样本数。

#### 2.1.2 精确率的概念和应用场景
精确率（Precision）是衡量模型预测为正类的样本中，实际为正类的比例。精确率的计算公式为：

\[ \text{Precision} = \frac{\text{正确预测为正类的样本数量}}{\text{预测为正类的样本总数}} \]

精确率适用于那些更关注预测为正类别时的正确性问题。例如，在垃圾邮件分类中，我们更希望减少将正常邮件错误地标记为垃圾邮件的情况，因为这可能导致信息的丢失。在这种情况下，精确率就是一个重要的评估指标。

精确率通常与其他指标（如召回率）一起使用，以提供更全面的模型评估。准确度、精确率和召回率之间的关系及其在不同应用中的重要性将在后续章节进行深入探讨。

### 2.2 召回率与F1分数

#### 2.2.1 召回率的含义和重要性
召回率（Recall），也称为真阳性率，关注的是所有实际为正类的样本中，模型正确识别出来的比例。召回率的计算公式为：

\[ \text{Recall} = \frac{\text{正确预测为正类的样本数量}}{\text{实际为正类的样本总数}} \]

召回率在那些“漏报”（假阴性）代价很高的场景中特别重要。例如，在疾病诊断中，错过一个真实病例可能会导致严重的后果，因此在医疗领域中，模型的召回率就成为关键的性能指标。

召回率的优化通常会牺牲一些精确率，因为提高召回率意味着将更多的样本预测为正类，这可能会导致更多的错误分类。因此，在实际应用中，需要根据具体需求权衡精确率和召回率。

#### 2.2.2 F1分数的综合评估能力
F1分数是精确率和召回率的调和平均数，它综合考虑了两者的关系，并试图找到一个平衡点。F1分数的计算公式如下：

\[ F1 = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}} \]

F1分数的最大值为1，当精确率和召回率都为1时取得，最小值为0。F1分数特别适用于那些精确率和召回率同样重要的分类任务。通过计算F1分数，可以避免在提高精确率的同时过分降低召回率，或者在提高召回率的同时过分降低精确率。

### 2.3 ROC曲线与AUC值

#### 2.3.1 ROC曲线的绘制方法
ROC曲线（Receiver Operating Characteristic curve）是一种评价分类模型性能的有效工具，它通过将真正率（True Positive Rate，与召回率相同）与假正率（False Positive Rate）绘制在同一张图上，从而展现出模型在不同阈值下的表现。

绘制ROC曲线的步骤如下：
1. 在不同阈值设置下，计算模型对正类和负类的预测概率。
2. 从高到低设置阈值，并分别计算每个阈值下的真正率和假正率。
3. 在ROC图上，以假正率为横坐标，真正率为纵坐标绘制曲线。

一般来说，ROC曲线越接近左上角，模型的分类性能越好。这是因为左上角对应的真正率高而假正率低。

#### 2.3.2 AUC值的意义和评价标准
AUC（Area Under Curve）值是ROC曲线下的面积，它提供了一个单一的数值来评价分类器的性能。AUC值的取值范围是0到1，其中：
- AUC值为1表示完美分类器，即模型在所有可能的正类样本中都有高于所有可能的负类样本的预测概率。
- AUC值为0.5表示随机分类器，即模型无法区分正负样本。

一般来说，AUC值在0.7以上认为模型具有较好的预测性能；AUC值在0.5到0.7之间表示模型的预测性能一般；而AUC值低于0.5则表明模型的预测性能不如随机猜测。AUC是评价二分类模型性能的一个强大工具，尤其在样本不平衡的场合中，它比准确度提供了更全面的信息。

通过精确度、召回率、F1分数、ROC曲线以及AUC值，我们可以从多个维度对分类模型进行评估，从而更全面地了解模型的性能表现。这些指标之间的关系以及如何选择合适的评估指标将在后续章节中进一步探讨。

# 3. 回归问题的评估指标

回归问题在机器学习和数据科学领域中是常见的问题类型之一，其目的是预测连续值输出。在回归问题中，评估指标帮助我们量化模型的预测性能。本章将详细探讨主要的回归问题评估指标，包括均方误差(MSE)、均方根误差(RMSE)、决定系数(R²)和平均绝对误差(MAE)，并深入理解偏差与方差的概念以及它们如何影响模型的性能。

## 3.1 均方误差(MSE)和均方根误差(RMSE)

### 3.1.1 均方误差的计算公式

均方误差（Mean Squared Error, MSE）是回归问题中最常用的性能指标之一。它计算了预测值和实际值之间差值的平方的平均值。MSE 的计算公式如下：

MSE = (1/n) * Σ(y_i - ŷ_i)²

其中 `y_i` 是实际值，`ŷ_i` 是预测值，而 `n` 是样本数量。代码示例如下：

import numpy as np

# 假设实际值和预测值
actual = np.array([1, 2, 3, 4, 5])
predicted = np.array([1.1, 1.9, 3.1, 4.1, 5.1])

# 计算 MSE
mse = np.mean((actual - predicted) ** 2)
print(f"MSE: {mse}")

MSE 对大误差的惩罚更大，因为它对误差进行了平方，因此，即使是非常小的误差也会被放大。模型的性能越好，MSE 的值越小。

### 3.1.2 均方根误差的特点及其优势

均方根误差（Root Mean Squared Error, RMSE）是MSE的平方根，它将误差的度量单位转换为与目标变量相同的单位，因此更易于理解和解释。RMSE的计算公式如下：

RMSE = √(MSE)

使用RMSE而不是MSE的主要优势在于其可解释性，因为RMSE提供了误差的实际范围。RMSE的代码实现如下：

import numpy as np

# 继续使用上面的 actual 和 predicted 变量

# 计算 RMSE
rmse = np.sqrt(np.mean((actual - predicted) ** 2))
print(f"RMSE: {rmse}")

RMSE是一个更易于解释的度量标准，它具有易于与原始数据的度量单位进行比较的优点，便于评估模型的性能。

## 3.2 决定系数(R²)和平均绝对误差(MAE)

### 3.2.1 决定系数的解释和应用场景

决定系数（R²）衡量的是模型对真实数据变异性的解释程度。它的取值范围是[0, 1]，值越接近1，表示模型对数据的拟合程度越好。R²计算公式如下：

R² = 1 - (SS_res / SS_tot)

其中 `SS_res` 是残差平方和，`SS_tot` 是总平方和。R²的代码实现：

from sklearn.metrics import r2_score

# 使用 sklearn 的 r2_score 函数计算
r2 = r2_score(actual, predicted)
print(f"R²: {r2}")

R²在回归问题的评估中非常有用，尤其在比较不同模型的性能时。一个模型如果在