SVM核函数的深入理解与应用：从基础到高级

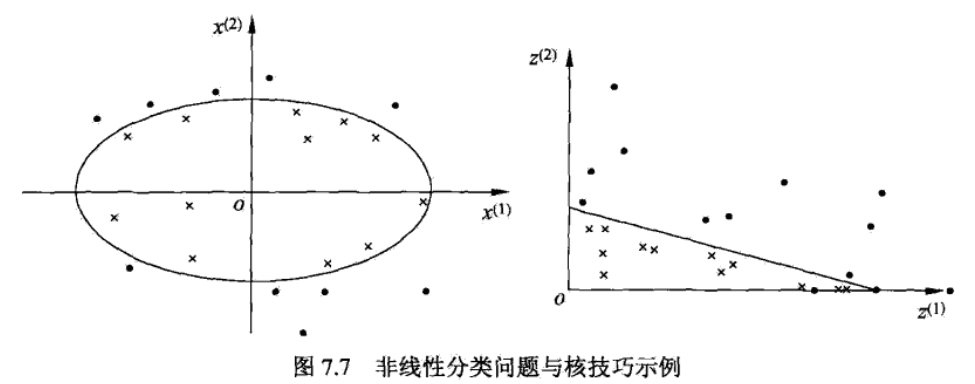
# 1. SVM核函数基础**

支持向量机（SVM）是一种强大的机器学习算法，用于解决分类和回归问题。SVM核函数是SVM算法的关键组成部分，它将低维输入数据映射到高维特征空间，从而使线性不可分的数据集在高维空间中变得线性可分。

**1.1 核函数的定义**

核函数是一个函数，它接受两个输入向量x和y，并输出一个标量值。核函数的目的是衡量x和y之间的相似性或距离。常用的核函数包括线性核函数、多项式核函数和高斯核函数。

**1.2 核函数的性质**

核函数具有以下性质：

* **对称性：** K(x, y) = K(y, x)
* **正定性：** 对于任何x和y，K(x, x) >= 0
* **平移不变性：** 对于任何x、y和b，K(x + b, y + b) = K(x, y)

# 2.1 线性核函数

**2.1.1 定义**

线性核函数是SVM中最简单的核函数，其定义如下：

K(x, y) = x^T y

其中，x和y是输入空间中的两个向量。

**2.1.2 几何解释**

线性核函数的几何解释是计算两个向量之间的点积。点积衡量两个向量在方向上的一致性，其值越大，则两个向量越相似。

**2.1.3 参数分析**

线性核函数没有可调参数，因此不需要进行参数调优。

**2.1.4 优点**

* 计算效率高
* 内存消耗低
* 适用于线性可分数据集

**2.1.5 缺点**

* 对于非线性可分数据集，线性核函数无法有效将数据映射到高维空间。

## 2.2 多项式核函数

**2.2.1 定义**

多项式核函数是一种非线性核函数，其定义如下：

K(x, y) = (x^T y + c)^d

其中，c和d是可调参数。

**2.2.2 几何解释**

多项式核函数将输入空间映射到一个更高维的空间，其中两个向量之间的相似性由它们在这个高维空间中的距离决定。

**2.2.3 参数分析**

多项式核函数有两个可调参数：

* **c：**平移参数，控制核函数的中心位置。
* **d：**度数，控制映射到高维空间的维度。

**2.2.4 优点**

* 适用于非线性可分数据集
* 可以通过调整参数来控制映射到高维空间的维度

**2.2.5 缺点**

* 计算复杂度较高
* 容易过拟合

## 2.3 高斯核函数

**2.3.1 定义**

高斯核函数是一种径向基核函数，其定义如下：

K(x, y) = exp(-γ||x - y||^2)

其中，γ是可调参数。

**2.3.2 几何解释**

高斯核函数将输入空间映射到一个无限维的空间，其中两个向量之间的相似性由它们在这个无限维空间中的距离决定。

**2.3.3 参数分析**

高斯核函数有一个可调参数：

* **γ：**带宽参数，控制核函数的局部性。γ越大，核函数越局部，反之亦然。

**2.3.4 优点**

* 适用于非线性可分数据集
* 对噪声数据具有鲁棒性
* 计算复杂度中等

**2.3.5 缺点**

* 容易过拟合
* 内存消耗较高

# 3.1 核函数在分类中的应用

核函数在分类中的应用主要分为线性可分数据集和线性不可分数据集两种情况。

#### 3.1.1 线性可分数据集

对于线性可分数据集，可以使用线性核函数进行分类。线性核函数的数学表达式为：

K(x, y) = x^T y

其中，x和y是两个数据点。

线性核函数将数据点直接映射到特征空间，而不改变其原始维度。因此，对于线性可分数据集，使用线性核函数可以将数据点正确分类。

#### 3.1.2