揭秘SVM分类算法：数学原理与代码实现

# 1. SVM分类算法概述**

支持向量机（SVM）是一种强大的分类算法，因其在高维数据和非线性问题上的卓越表现而闻名。SVM的目标是找到一个超平面，将数据点以最佳方式分开，最大化超平面与数据点的间隔。

SVM通过将数据点映射到高维空间，将线性不可分问题转换为线性可分问题。在高维空间中，数据点可以用超平面完美分开，从而实现分类。SVM算法的核心思想是找到使超平面与数据点间隔最大的超平面，称为最大间隔超平面。

# 2. SVM分类算法的数学原理

### 2.1 线性可分支持向量机

#### 2.1.1 硬间隔最大化

对于线性可分的数据集，SVM的目标是找到一个超平面，将两类数据点完全分开。这个超平面的方程可以表示为：

w^T x + b = 0

其中：

- `w` 是超平面的法向量
- `x` 是数据点
- `b` 是超平面的截距

为了找到最佳超平面，SVM采用硬间隔最大化的策略。硬间隔是指超平面到最近数据点的距离。最大化硬间隔可以确保超平面具有最大的容错性，即能够正确分类所有数据点。

硬间隔最大化的数学模型可以表示为：

max w,b 1/||w||
s.t. y_i (w^T x_i + b) >= 1, i = 1, ..., n

其中：

- `||w||` 是 `w` 的 L2 范数，表示超平面的法向量的长度
- `y_i` 是第 `i` 个数据点的标签（+1 或 -1）
- `x_i` 是第 `i` 个数据点的特征向量

#### 2.1.2 软间隔最大化

在实际应用中，数据集可能不是完全线性可分的。为了处理这种情况，SVM引入了软间隔的概念。软间隔允许数据点违反超平面，但会受到惩罚。

软间隔最大化的数学模型可以表示为：

max w,b 1/||w|| + C ∑_{i=1}^n \xi_i
s.t. y_i (w^T x_i + b) >= 1 - \xi_i, i = 1, ..., n
\xi_i >= 0, i = 1, ..., n

其中：

- `C` 是正则化参数，控制惩罚项的权重
- `\xi_i` 是第 `i` 个数据点的松弛变量，表示数据点违反超平面的程度

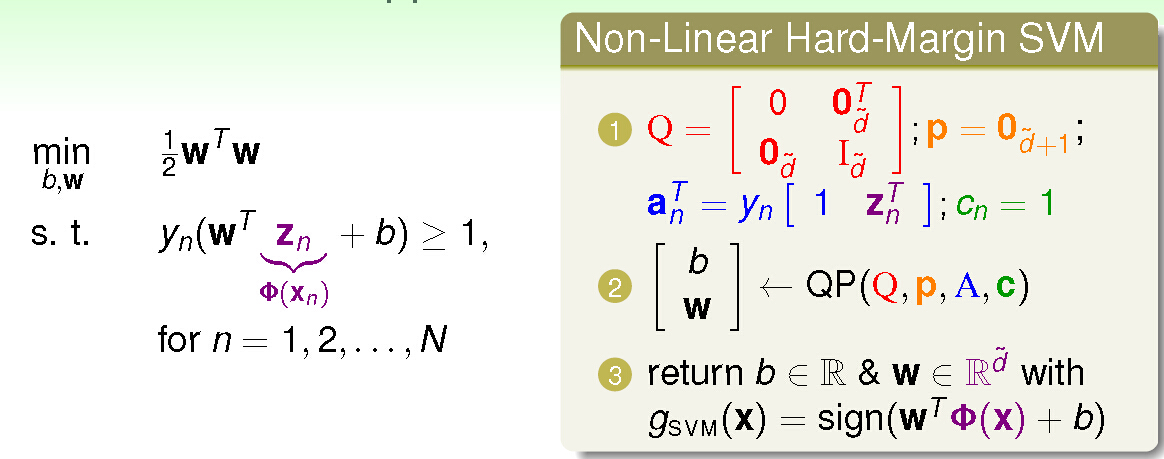
### 2.2 非线性可分支持向量机

对于非线性可分的数据集，SVM采用核函数将数据映射到更高维度的特征空间，使其在该空间中线性可分。

#### 2.2.1 核函数

核函数是一个函数，它将两个数据点映射到一个更高维度的特征空间。常用的核函数包括：

- 线性核函数：`K(x, y) = x^T y`
- 多项式核函数：`K(x, y) = (x^T y + c)^d`
- 高斯核函数：`K(x, y) = exp(-γ ||x - y||^2)`

#### 2.2.2 核技巧

核技巧是一种数学技巧，它允许我们在不显式地映射数据的情况下计算核函数。这大大提高了SVM在高维特征空间中的计算效率。

核技巧的数学公式为：

K(x, y) = φ(x)^T φ(y)

其中：

- `φ(x)` 是数据点 `x` 在特征空间中的映射
- `K(x, y)` 是核函数

# 3.1 Python中SVM分类器的使用

#### 3.1.1 scikit-learn库

scikit-learn是Python中广泛使用的机器学习库，它提供了SVM分类器的实现。要使用scikit-learn中的SVM分类器，可以按以下步骤进行：

from sklearn.svm import SVC

# 创建一个SVM分类器
clf = SVC()

# 训练SVM分类器
clf.fit(X_train, y_train)

# 使用SVM分类器进行预测
y_pred = clf.predict(X_test)

**参数说明：**

* `C`：软间隔参数，控制对误分类的惩罚程度。
* `kernel`：核函数类型，用于将非线性数据映射到高维空间。
* `degree`：核函数的次数（仅适用于多项式核函数）。
* `gamma`：核函数的系数（仅适用于RBF和sigmoid核函数）。

**代码逻辑分析：**

1. 创建一个SVM分类器对象，并设置所需的超参数。
2. 调用`fit()`方法训练SVM分类器，使用训练数据`X_train`和目标标签`y_train`。
3. 调用`predict()`方法使用测试数据`X_test`进行预测，并存储预测结果在`y_pred`中。

#### 3.1.2 参数调优

参数调优对于提高SVM分类器的性能至关重要。scikit-learn提供了`GridSearchCV`类，可以方便地进行网格搜索参数调优。

from sklearn.model_selection import GridSearchCV

# 设置要调优的参数
param_grid = {'C': [0.1, 1, 10], 'kernel': ['linear', 'rbf'], 'gamma': [0.1, 1, 10]}

# 创建网格搜索对象
grid_search = GridSearchCV(clf, param_grid, cv=5)

# 执行网格搜索
grid_search.fit(X_train, y_train)

# 获取最佳超参数
best_params = grid_search.best_params_

**参数说明：**

* `param_grid`：要调优的参数及其候选值。
* `cv`：交叉验证的折数。

**代码逻辑分析：**

1. 定义要调优的参数及其候选值，并存储在`param_grid`中。
2. 创建一个`GridSearchCV`对象，指定要调优的分类器、参数网格和交叉验证折数。
3. 调用`fit()`方法执行网格搜索，使用训练数据`X_train`和目标标签`y_train`。
4. 获取最佳超参数，存储在`best_params`中。

# 4. SVM分类算法的应用**

SVM分类算法在实际应用中有着广泛的应用场景，其中包括文本分类和图像分类。

**4.1 文本分类**

文本分类是指将文本文档自动分配到预定义的类别中。SVM分类算法在文本分类任务中表现出色，主要原因在于其能够有效处理高维稀疏数据，并且具有良好的泛化能力。

**4.1.1 特征提取**

文本分类的第一步是特征提取，即从文本文档中提取有用的特征。常用的文本特征包括：

- **词袋模型 (Bag-of-Words)**：将文本文档表示为单词的集合，每个单词的出现次数作为特征值。
- **TF-IDF (Term Frequency-Inverse Document Frequency)**：考虑单词在文档中出现的频率和在语料库中出现的频率，赋予每个单词不同的权重。
- **N-gram 模型**：将文本文档表示为连续的单词序列，每个序列作为特征值。

**4.1.2 模型训练和评估**

特征提取完成后，即可使用SVM分类器进行模型训练。常用的SVM核函数包括：

- **线性核函数**：适用于线性可分的数据。
- **多项式核函数**：适用于非线性可分的数据。
- **径向基核函数 (RBF)**：适用于高维非线性数据。

模型训练完成后，需要对模型进行评估。常用的评估指标包括：

- **准确率**：正确分类的样本数与总样本数之比。
- **召回率**：正确分类的正样本数与实际正样本数之比。
- **F1 分数**：准确率和召回率的加权平均值。

**4.2 图像分类**

图像分类是指将图像自动分配到预定义的类别中。SVM分类算法在图像分类任务中也表现出色，主要原因在于其能够有效处理高维数据，并且具有良好的鲁棒性。

**4.2.1 图像预处理**

图像分类的第一步是图像预处理，即对图像进行必要的处理，以增强特征提取的效果。常用的图像预处理技术包括：

- **图像缩放**：将图像缩放至统一大小。
- **灰度化**：将彩色图像转换为灰度图像。
- **直方图均衡化**：增强图像的对比度。

**4.2.2 模型训练和评估**

图像预处理完成后，即可使用SVM分类器进行模型训练。常用的图像特征包括：

- **颜色直方图**：计算图像中不同颜色的出现频率。
- **纹理特征**：提取图像中的纹理信息，如边缘、斑点和纹理。
- **形状特征**：提取图像中的形状信息，如轮廓、面积和周长。

模型训练完成后，需要对模型进行评估。常用的评估指标包括：

- **准确率**：正确分类的图像数与总图像数之比。
- **混淆矩阵**：显示了实际类别和预测类别之间的关系。
- **ROC 曲线**：显示了模型在不同阈值下的真阳率和假阳率。

# 5. SVM分类算法的优化**

**5.1 参数调优**

SVM分类算法的性能受多种参数影响，包括核函数类型、核参数和正则化参数。参数调优的目标是找到一组最优参数，以最大化分类精度。

**5.1.1 网格搜索**

网格搜索是一种广泛使用的参数调优方法。它涉及在参数空间中定义一个网格，并对每个参数组合训练和评估模型。最佳参数组合是具有最高分类精度的组合。

from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC

# 定义参数网格
param_grid = {'kernel': ['linear', 'rbf'],
               'C': [0.1, 1, 10],
               'gamma': ['auto', 'scale']}

# 创建 SVM 分类器
svm = SVC()

# 执行网格搜索
grid_search = GridSearchCV(svm, param_grid, cv=5)
grid_search.fit(X_train, y_train)

# 获取最优参数
best_params = grid_search.best_params_

**5.1.2 贝叶斯优化**

贝叶斯优化是一种更高级的参数调优方法。它使用贝叶斯定理来指导参数搜索，并根据先前的结果调整参数分布。

from bayes_opt import BayesianOptimization

# 定义目标函数
def objective(params):
    svm = SVC(**params)
    svm.fit(X_train, y_train)
    return svm.score(X_test, y_test)

# 定义参数边界
bounds = {'kernel': ['linear', 'rbf'],
           'C': (0.1, 10),
           'gamma': (0.1, 10)}

# 执行贝叶斯优化
optimizer = BayesianOptimization(f=objective, pbounds=bounds)
optimizer.maximize(n_iter=10)

# 获取最优参数
best_params = optimizer.max['params']

**5.2 模型选择**

参数调优后，下一步是选择最合适的模型。模型选择涉及评估不同模型的性能，并选择具有最高泛化能力的模型。

**5.2.1 交叉验证**

交叉验证是一种评估模型泛化能力的常用技术。它将数据集划分为多个子集，然后使用其中一个子集作为测试集，其余子集作为训练集。此过程重复多次，并计算模型在所有子集上的平均性能。

from sklearn.model_selection import cross_val_score

# 创建 SVM 分类器
svm = SVC()

# 执行交叉验证
scores = cross_val_score(svm, X, y, cv=5)

# 计算平均准确率
accuracy = np.mean(scores)

**5.2.2 模型融合**

模型融合是一种将多个模型的预测结果结合起来以提高性能的技术。对于 SVM 分类，可以将多个内核或正则化参数的模型融合起来。

from sklearn.ensemble import VotingClassifier

# 创建 SVM 分类器
svm1 = SVC(kernel='linear', C=1)
svm2 = SVC(kernel='rbf', C=10, gamma=0.1)

# 创建投票分类器
voting_clf = VotingClassifier(estimators=[('svm1', svm1), ('svm2', svm2)], voting='hard')

# 训练投票分类器
voting_clf.fit(X_train, y_train)

# 评估投票分类器
accuracy = voting_clf.score(X_test, y_test)