MATLAB指数分布随机数生成：揭秘指数分布随机数生成算法，提升算法鲁棒性

# 1. 指数分布简介

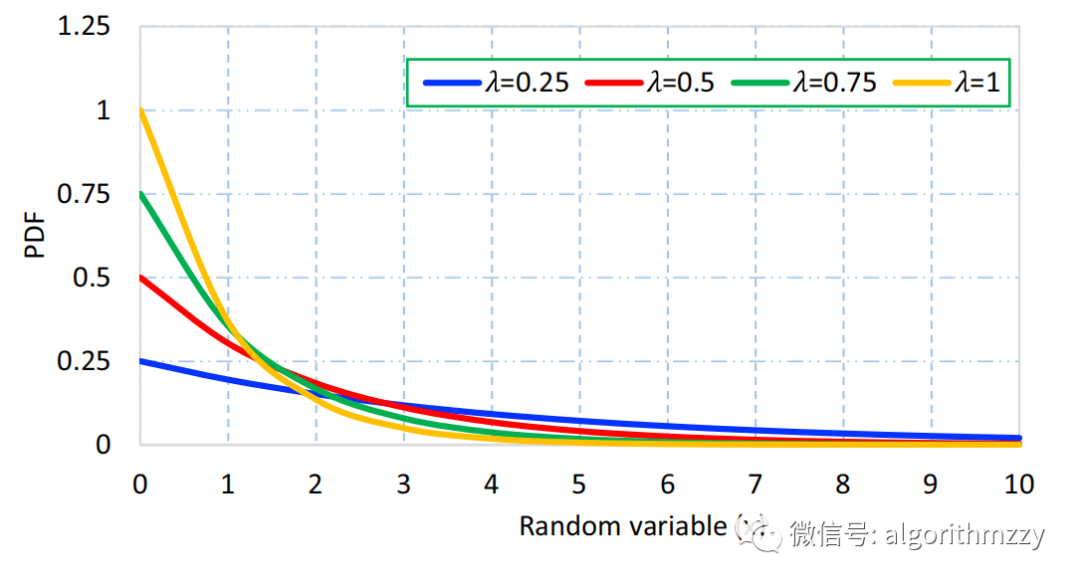
指数分布是一种连续概率分布，其概率密度函数为 f(x) = λ * exp(-λ * x)，其中 λ 为正实数参数，表示分布的速率。指数分布广泛应用于各种领域，例如故障时间建模、金融建模和排队论。

指数分布的期望值和方差分别为 1/λ 和 1/λ^2。其累积分布函数 (CDF) 为 F(x) = 1 - exp(-λ * x)，逆累积分布函数 (ICDF) 为 x = -log(1 - u)/λ，其中 u 为 [0, 1] 上的均匀分布随机变量。

# 2. 指数分布随机数生成算法

### 2.1 逆变换法

#### 2.1.1 基本原理

逆变换法是生成随机数的一种经典方法，其基本原理是利用随机变量的累积分布函数（CDF）的反函数来生成随机数。对于指数分布，其CDF为：

F(x) = 1 - exp(-λx)

其中，λ为指数分布的参数。

逆变换法的具体步骤如下：

1. 生成一个均匀分布的随机数u。
2. 求解CDF的反函数：x = F^(-1)(u)。
3. 将u代入F^(-1)(u)中，得到指数分布的随机数x。

#### 2.1.2 MATLAB实现

在MATLAB中，可以使用`unifrnd`函数生成均匀分布的随机数，并使用`log`函数求解CDF的反函数。具体代码如下：

function x = exp_inv(lambda)
    u = unifrnd(0, 1);
    x = -log(u) / lambda;
end

### 2.2 接受-拒绝法

#### 2.2.1 基本原理

接受-拒绝法是一种用于生成任意分布的随机数的方法。其基本原理是：

1. 找到一个比目标分布更容易采样的辅助分布。
2. 根据辅助分布生成一个候选样本。
3. 根据候选样本的概率密度比，决定是否接受该样本。

对于指数分布，一个合适的辅助分布是均匀分布。

#### 2.2.2 MATLAB实现

在MATLAB中，可以使用`unifrnd`函数生成均匀分布的随机数。具体代码如下：

function x = exp_rej(lambda)
    while true
        u = unifrnd(0, 1);
        v = unifrnd(0, lambda);
        if v <= lambda * exp(-lambda * u)
            x = u;
            break;
        end
    end
end

# 3.1 算法稳定性分析

#### 3.1.1 算法收敛性

逆变换法和接受-拒绝法都是基于概率分布的性质进行随机数生成，因此算法的收敛性取决于概率分布的性质。对于指数分布，其概率密度函数为：

f(x) = λ * exp(-λ * x)

其中，λ 为指数分布的速率参数。

**逆变换法**

逆变换法的收敛性依赖于概率分布的累积分布函数 (CDF) 的单调性。指数分布的 CDF 为：

F(x) = 1 - exp(-λ * x)

该函数是单调递增的，因此逆变换法在指数分布随机数生成中具有收敛性。

**接受-拒绝法**

接受-拒绝法的收敛性取决于提议分布的形状和参数选择。对于指数分布，通常选择均匀分布或正态分布作为提议分