特征提取高级技术：核方法与算法性能的联动

# 1. 核方法在特征提取中的基础理论

## 1.1 核方法概念与重要性
核方法是一种强大的数学工具，用于处理和分析高维数据。它通过将原始数据映射到高维空间，使原本在低维空间中线性不可分的数据在新的空间中能够线性区分。这种方法在特征提取中尤为重要，因为它可以揭示数据中更深层次的结构和关系。

## 1.2 核技巧的数学原理
核技巧的核心在于核函数的应用，通过核函数我们能够计算在高维空间中数据点的内积，而无需显式地进行维度提升。这种方法不仅简化了计算，还允许我们在高维空间中有效地应用各种机器学习算法。

## 1.3 特征提取中的核方法应用
在特征提取领域，核方法通过隐式地将原始数据映射到一个高维空间，使得复杂特征变得更加明显和易于区分。这在处理图像识别、文本分析等复杂数据时尤为重要，能够大幅提高机器学习模型的准确性和效率。

# 2. ```
# 第二章：核方法的关键算法与理论

## 2.1 核函数的种类与选择

### 2.1.1 线性核函数的原理与应用

线性核函数是最简单的核函数类型，它基于原始特征空间中的点积运算。其数学表达式通常为：

\[ K(x, y) = x^T y \]

其中，\( x \)和\( y \)为两个样本向量。在许多机器学习算法中，线性核函数被用于数据的线性特征提取和分类任务。由于其计算简单，易于实现，线性核函数被广泛应用于线性可分的问题中，比如逻辑回归和线性支持向量机。

在实际应用中，选择线性核函数意味着不需要将数据映射到高维特征空间，从而避免了复杂的核技巧。但这也会限制模型的能力，因为线性核无法捕捉数据中的非线性关系。因此，当面对复杂模式或非线性问题时，线性核可能不是最佳选择。

### 2.1.2 非线性核函数的特性分析

非线性核函数允许算法在高维空间中工作，而无需显式地计算数据点在该空间中的坐标。最常用的非线性核函数包括多项式核和径向基函数（RBF）核。

多项式核函数的一般形式如下：

\[ K(x, y) = (x^T y + c)^d \]

其中，\( c \)和\( d \)为超参数，决定了多项式的阶数和截距。多项式核能够生成非线性决策边界，并且通过调整\( c \)和\( d \)的值，可以控制模型的复杂度。

径向基函数核（RBF核），也称为高斯核，是一种局部性核函数，其表达式为：

\[ K(x, y) = e^{-\gamma \|x - y\|^2} \]

\( \gamma \)是控制核函数宽度的超参数。RBF核能够捕捉数据点之间的相似度，且对数据的局部结构敏感。在许多情况下，RBF核展现出了出色的性能，尤其在数据点之间的距离在高维空间中起关键作用时。

## 2.2 核主成分分析(KPCA)

### 2.2.1 KPCA的数学基础

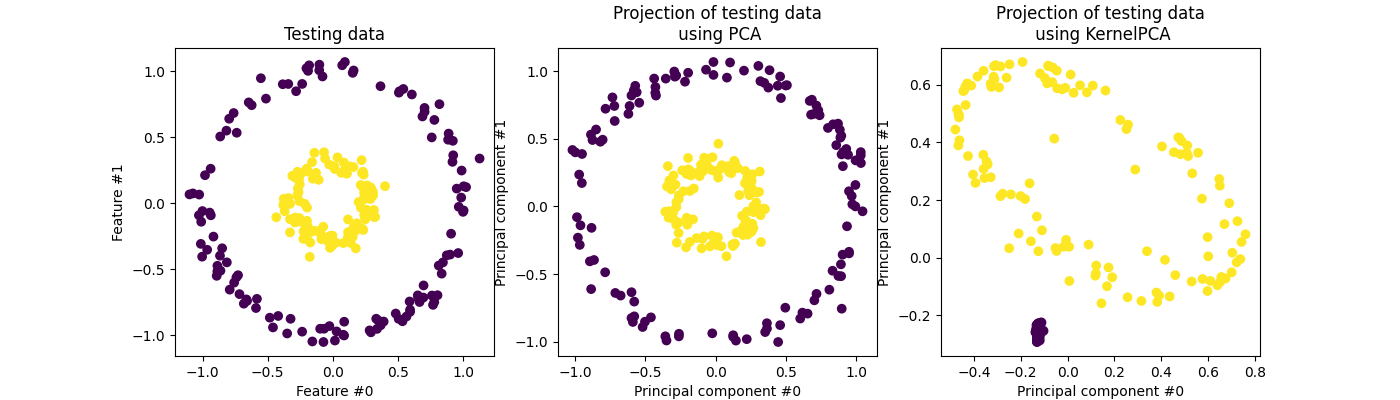
核主成分分析（KPCA）是一种非线性降维技术，其基本思想是将数据映射到高维空间中，然后在该空间中进行主成分分析。与传统的PCA不同，KPCA通过核函数隐式地实现了这种映射，从而避免了复杂的非线性映射的直接计算。

KPCA的核心在于，首先通过一个非线性映射函数将原始数据映射到高维特征空间，接着在这个高维空间中执行线性PCA。数学上，这可以表示为最大化数据协方差矩阵的特征值，找到数据的主成分方向。

### 2.2.2 KPCA的实现步骤与应用场景

KPCA的实现步骤如下：

1. 选择合适的核函数并计算核矩阵。
2. 中心化核矩阵，即减去核矩阵的每一行和每一列的平均值。
3. 计算中心化核矩阵的特征值和特征向量。
4. 选择主成分，即保留最大的几个特征值对应的特征向量。
5. 将原始数据投影到这些特征向量上，获得降维后的数据。

KPCA特别适用于数据集存在非线性关系时，可以发现比PCA更多的复杂结构。它在图像处理、生物信息学以及高维数据可视化等领域有广泛应用。

## 2.3 支持向量机(SVM)

### 2.3.1 SVM的理论基础与核技巧

支持向量机（SVM）是一种强大的监督学习算法，主要用于分类和回归分析。它的基本思想是找到一个最优的决策边界，即超平面，使得不同类别的数据之间有最大的间隔（margin）。

SVM通过核技巧可以扩展到非线性可分数据。核技巧的基本思想是使用一个非线性映射将数据映射到高维特征空间，在这个空间中找到线性分割超平面。核函数在SVM中用于计算数据点映射到高维空间后的内积，而无需显式地进行映射。

核函数的选择对于SVM模型的性能至关重要。常用的核函数包括线性核、多项式核、RBF核和sigmoid核。每种核函数有其特定的参数，如RBF核中的\( \gamma \)参数和多项式核中的\( c \)和\( d \)参数，这些参数需要通过模型选择过程来优化。

### 2.3.2 SVM在特征提取中的高级应用

在特征提取中，SVM不仅可以用来分类数据，还可以用来确定哪些特征对于分类任务最为重要。这一过程通常涉及特征选择技术，如递归特征消除（RFE）。

SVM在特征提取中的高级应用包括：

- 使用SVM的权重向量作为特征重要性的指示器。
- 通过RFE迭代移除对决策边界的贡献最小的特征。
- 通过核技巧增强SVM模型对非线性特征组合的识别能力。

此外，SVM模型可以与其他机器学习模型相结合，如在集成学习中作为基学习器，以提升整体的预测性能。在实际应用中，SVM的高级应用需要结合具体问题进行定制化的模型调优和特征工程。

在下一章节中，我们将深入探讨核方法在数据挖掘中的实践应用，包括文本挖掘、图像处理以及生物信息学中的应用案例和分析。

以上为第二章核方法的关键算法与理论的内容，接下来将展示第三章核方法在数据挖掘中的实践应用的内容。

# 3. 核方法在数据挖掘中的实践应用

## 3.1 文本挖掘中的核方法应用

### 3.1.1 核方法在文本分类中的角色

在文本挖掘领域，核方法提供了一种有效的方式来处理高维数据的非线性问题。文本数据往往以词频向量或TF-IDF向量的形式存在，这些向量在高维空间中是稀疏的。核方法，尤其是支持向量机(SVM)，能够将这些高维数据映射到特征空间，并在此空间中使用线性分类器对文本进行分类。

核方法在文本分类中的角色主要体现在以下几个方面：

1. **特征空间映射**：通过核函数将原始的高维向量映射到一个更为丰富、能够捕捉数据非线性结构的特征空间。
2. **内积计算简化**：核函数使得在特征空间中无需显式计算向量的内积，直接通过核函数计算即可。
3. **非线性分类能力**：允许使用线性分类算法在特征空间中实现复杂的非线性分类。
4. **维数灾难缓解**：核方法无需直接处理高维数据，从而避免了维数灾难。

### 3.1.2 实例分析：新闻文本数据的特征提取

为了更具体地理解核方法在文本分类中的应用，我们考虑一个新闻文本数据的分类问题。在这个案例中，我们使用核支持向量机(KSVM)来对新闻文本进行分类。

#### 步骤一：数据预处理

首先，对新闻文本数据进行预处理，包括：

- 分词处理：将文本分割成独立的词汇。
- 去除停用词：删除常见的无意义词汇。
- 词干提取：将词汇还原到词根形式。
- 向量化：将处理后的文本转换为TF-IDF向量。

#### 步骤二：选择核函数

接下来，选择适当的核函数。常用的核函数包括线性核、多项式核和高斯径向基函数(RBF)核。在文本挖掘中，RBF核通常能获得较好的结果，因为它能够处理向量间的非线性关系。

#### 步骤三：核支持向量机训练

使用选定的核函数，训练一个核支持向量机模型。在这个过程中，我们会使用训练数据来确定模型的参数。

from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.svm import SVC
from sklearn.pipeline import make_pipeline

# 假设 `texts` 是新闻文本数据列表，`labels` 是对应的分类标签
pipeline = make_pipeline(TfidfVectorizer(), SVC(kernel='rbf'))
pipeline.fit(texts, labels)

#### 步骤四：模型评估

最后，使用验证数据集评估模型性能。常用的评估指标包括准确度、精确度、召回率和F1分数。

from sklearn.metrics import classification_report

# 假设 `texts_val` 是验证集中的新闻文本数据列表，`labels_val` 是对应的分类标签
predictions = pipeline.predict(texts_val)
print(classification_report(labels_val, predictions))

通过上述步骤，核方法在文本分类中的应用得以体现。在实际操作中，为了获得更好的分类效果，可能需要对模型的参数进行调整，包括选择不同的核函数、调整SVM的惩罚参数C以及RBF核的γ参数等。

## 3.2 图像处理中的核方法应用

### 3.2.1 核方法在图像特征提取中的作用

在图像处理领域，核方法可以被用于提取图像的特征，并进行图像分类、识别等任务。图像数据通常是高维的，并且包含复杂的空间结构，使得传统的线性方法难以处理。核方法能够映射图像数据到高维空间，并在该空间中寻找线性可分的模式。

核方法在图像特征提取中的作用可以总结为以下几点：

1. **非线性映射**：通过核技巧，将图像数据非线性地映射到高维空间，以便捕捉更加复杂的结构。
2. **特征增强**：在映射后的空间中，原本在原始空间中不可区分的图像可能变得线性可分，从而增强了特征的区分能力。
3. **核聚类**：