【深度学习与监督学习】：实战指南，选择最合适的算法

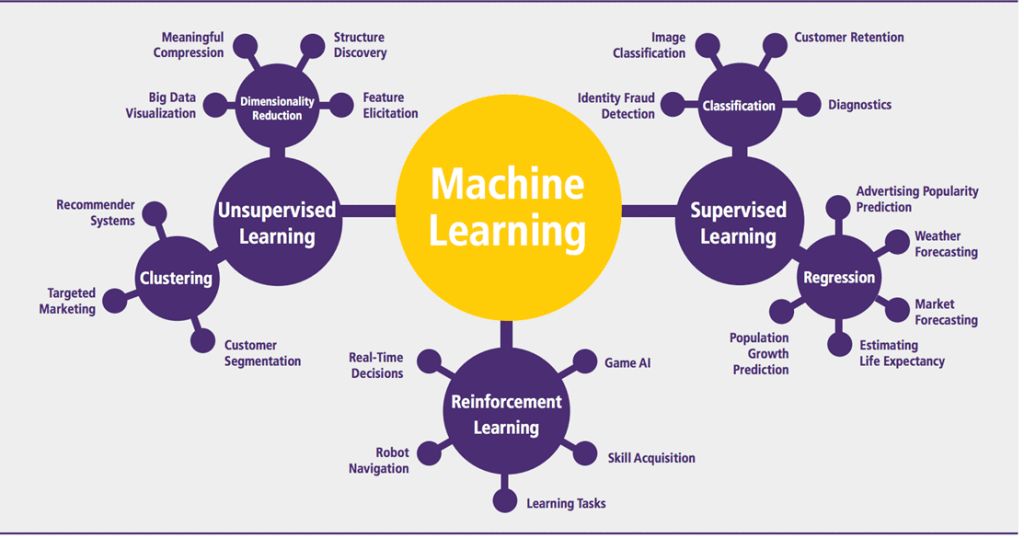
# 1. 深度学习基础与监督学习概述

深度学习是人工智能领域的一项突破性技术，它通过模仿人脑神经网络的工作方式构建和训练多层神经网络，从而实现对数据的高级抽象和特征学习。而监督学习作为机器学习的一个重要分支，它依赖于带有标签的数据集来训练模型，以便进行预测或分类任务。在本章中，我们将探讨深度学习与监督学习之间的联系，以及它们在现代IT行业中的重要性和应用。

## 1.1 深度学习的兴起
深度学习的概念早在上世纪就已存在，但由于数据量和计算能力的限制，直到近年来才迎来了快速发展。大规模数据集的可用性和图形处理单元（GPU）的强大计算能力，使深度学习在图像识别、语音识别、自然语言处理等多个领域取得了显著的成功。

## 1.2 监督学习的角色
在监督学习中，算法通过输入输出对（训练数据）进行学习，以预测或分类新的、未见过的数据。监督学习的算法包括线性回归、逻辑回归、支持向量机（SVM）和决策树等。这些方法为深度学习模型提供了理论基础，并且在很多情况下仍然是有效的工具。

## 1.3 深度学习与监督学习的融合
随着深度学习技术的发展，它与传统的监督学习方法相结合，产生了新的模型和算法。例如，深度神经网络可以看作是多层的、非线性的逻辑回归模型。这种融合不仅增强了模型的学习能力，而且也促进了监督学习在复杂数据处理中的应用。

通过本章的学习，读者将对深度学习和监督学习有一个基础的了解，并为接下来的章节打下坚实的基础。

# 2. 监督学习算法的理论基础

### 2.1 监督学习的基本概念
监督学习是机器学习的一个子领域，它涉及训练计算机算法来学习数据间的模式，以便做出预测或决策。在这一过程中，算法会从标注的训练数据中学习，并应用这些学习到新的、未标注的数据上。

#### 2.1.1 监督学习定义及分类
监督学习可定义为一种机器学习方法，它根据输入数据（特征）及其相应的输出（标签）来训练模型。这种方法使得模型能够学习如何准确地预测新输入数据的输出值。监督学习的分类包括回归问题（预测连续值）和分类问题（预测离散值）。

在回归问题中，目标是预测一个数值，如房价预测或股票价格预测。而在分类问题中，目标是将数据分配到预定的类别，如邮件是否是垃圾邮件的二分类问题，或衣服的尺寸（S、M、L、XL）的多分类问题。

#### 2.1.2 训练集、测试集与验证集的作用
为了评估监督学习模型的性能，数据被分为训练集、测试集和验证集。训练集用来训练模型，测试集用来评估模型性能，而验证集用于在模型训练过程中进行超参数的调整。

训练集是模型学习的基础，包含了输入数据和对应的输出标签。测试集用来在模型训练完成后评估模型的泛化能力，即模型对于未知数据的预测能力。验证集用于在模型的训练过程中调整模型参数，避免过拟合，并选择最佳的模型结构。

### 2.2 线性回归与逻辑回归
#### 2.2.1 线性回归模型的原理与实现
线性回归是监督学习中最基础的算法之一，用于预测连续值。它假设输入变量和输出变量之间存在线性关系。在二维空间中，这种关系可以表示为一条直线。

线性回归模型的实现通常采用最小二乘法。基本公式为 `y = wx + b`，其中 `y` 是预测值，`x` 是输入变量，`w` 是模型参数（权重），`b` 是偏置项。权重和偏置项是通过训练数据拟合得到的。

import numpy as np

# 示例数据
X = np.array([[1], [2], [3], [4]])
Y = np.array([2, 4, 6, 8])

# 简单线性回归模型
class LinearRegression:
    def __init__(self):
        self.weights = None

    def fit(self, X, Y):
        # 使用最小二乘法计算权重
        self.weights = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(Y)

    def predict(self, X):
        return X.dot(self.weights)

# 训练模型
model = LinearRegression()
model.fit(X, Y)

# 预测结果
print(model.predict(X))

该代码块展示了如何实现一个简单的线性回归模型。

#### 2.2.2 逻辑回归模型及其在分类问题中的应用
逻辑回归是一种广泛应用于二分类问题的监督学习算法。尽管名字中包含“回归”，它实际上是一种分类算法。逻辑回归的核心是使用逻辑函数（如sigmoid函数）对线性回归的输出进行转换，使其能够输出一个介于0和1之间的概率值。

逻辑回归的模型公式可以表示为 `P(Y=1|X=x) = 1 / (1 + e^-(wx+b))`，其中 `P(Y=1|X=x)` 是给定输入 `x` 时，输出为1的概率。

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_classification

# 创建模拟分类数据
X, Y = make_classification(n_samples=1000, n_features=20, n_informative=2, n_redundant=10, random_state=42)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.2, random_state=42)

# 训练逻辑回归模型
logreg = LogisticRegression()
logreg.fit(X_train, y_train)

# 预测测试集
y_pred = logreg.predict(X_test)

该代码块使用了 `sklearn` 库中的 `LogisticRegression` 类训练一个逻辑回归模型。

### 2.3 支持向量机与决策树
#### 2.3.1 支持向量机的原理与核技巧
支持向量机（SVM）是一种强有力的监督学习算法，主要用于分类和回归问题。SVM的核心思想是找到一个超平面，最大化两个类别的边界。

核技巧是SVM的延伸技术，用于处理非线性可分数据。通过在高维空间中映射输入数据，使得原本在低维空间中非线性可分的数据变得线性可分。

from sklearn import datasets
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC

# 加载数据集
iris = datasets.load_iris()
X, y = iris.data, iris.target

# 建立SVM模型，使用核技巧
clf = make_pipeline(StandardScaler(), SVC(kernel='linear'))
clf.fit(X, y)

# 模型预测
y_pred = clf.predict(X)

这段代码展示了如何使用核技巧通过 `SVC` 类构建SVM模型。

#### 2.3.2 决策树的构建与剪枝策略
决策树是一种树形结构的分类或回归方法。在决策树中，每个内部节点表示一个属性上的测试，每个分支代表测试的结果，而每个叶节点代表一种类别。

剪枝是决策树优化中常见的策略，用于防止过拟合。剪枝策略通过移除树中一些对训练数据过度敏感的分支来提高模型泛化能力。

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn import tree
import matplotlib.pyplot as plt

# 加载数据集
iris = load_iris()
X, y = iris.data, iris.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)

# 训练决策树模型
clf = DecisionTreeClassifier(random_state=0, max_depth=4, min_samples_split=2)
clf.fit(X_train, y_train)

# 可视化决策树
plt.figure(figsize=(12,8))
tree.plot_tree(clf, filled=True)
plt.show()

以上代码演示了构建和可视化决策树模型的基本步骤。

以上就是第二章“监督学习算法的理论基础”的内容概要。接下来的章节将深入探讨深度学习的理论与实践。

# 3. 深度学习的理论与实践

深度学习是人工智能领域的一个重要分支，其核心是构建多层的神经网络模型来模拟人脑处理信息的机制，实现特征的自动提取与学习。在本章节中，我们将深入探讨深度学习的理论基础以及在实际应用中的实践操作。

## 3.1 神经网络的基本原理

### 3.1.1 人工神经网络结构简介

人工神经网络（Artificial Neural Network, ANN）是由大量的节点（或称神经元）之间互相连接构成的网络。这些节点被分成若干层，包括输入层、隐层（一个或多个）和输出层。每一层的神经元会根据输入数据，计算并传递信息到下一层。在前馈神经网络中，信息只会单向流动，从输入层到输出层，没有反馈连接。

神经网络的关键组件包括激活函数、权重、偏置和损失函数。激活函数用于引入非线性因素，确保网络可以学习复杂的模式。权重和偏置则是网络学习过程中的参数，它们在训练过程中通过优化算法不断调整。损失函数用于衡量模型的预测值与真实值之间的差异，指导网络进行参数优化。

### 3.1.2 前向传播与反向传播算法

前向传播是神经网络处理输入数据的过程，输入数据通过每一层的神经元，逐层进行加权求和和激活函数处理，最终到达输出层并产生预测结果。

反向传播算法是一种计算损失函数关于网络权重的梯度的方法。这一过程通常分为两步：首先，前向传播计算输出，然后计算损失函数值；接着，从输出层开始，逐步向隐层和输入层反向传播损失函数关于各个权重的梯度。利用梯度下降或其他优化算法，根据这些梯度更新网络的权重和偏置，以减少损失函数的值。

### 神经网络实现示例代码

以下是使用Python和TensorFlow框架构建一个简单的人工神经网络的示例代码，实现一个三分类问题。

import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense

# 构建模型
model = Sequential([
    Dense(12, activation='relu', input_shape=(input_size,)),
    Dense(8, activation='relu'),
    Dense(num_classes, activation='softmax') # 输出层，num_classes为分类数
])

# 编译模型
***pile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

# 训练模型
model.fit(x_train, y_train, epochs=10)

# 评估模型
loss, accuracy = model.evaluate(x_test, y_test)
print("Accuracy: %.2f%%" % (accuracy*100))

在这段代码中，`Sequential`用于构建序贯模型，`Dense`层表示全连接层。`input_shape`是输入层的参数，`num_classes`是输出层的单元数，对应于分类问题的类别数。损失函数使用的是`sparse_categorical_crossentropy`，适合多分类问题。模型使用`adam`优化器进行训练，并通过`fit`方法进行迭代。最后，使用`evaluate`方法评估模型的性能。

### 神经网络参数与逻辑分析

- `input_size`: 模型输入数据的特征维度。
- `num_classes`: 输出层的神经元数量，等于分类问题的类别数。
- `x_train, y_train`: 分别为训练数据的特征和标签。
- `x_test, y_test`: 分别为测试数据的特征和标签。

在训练模型时，参数`epochs`表示训练的轮数，每轮包含一次前向传播和一次反向传播。损失函数`spars