主成分分析（PCA）的正交性和方差最大化：深入理解降维原理

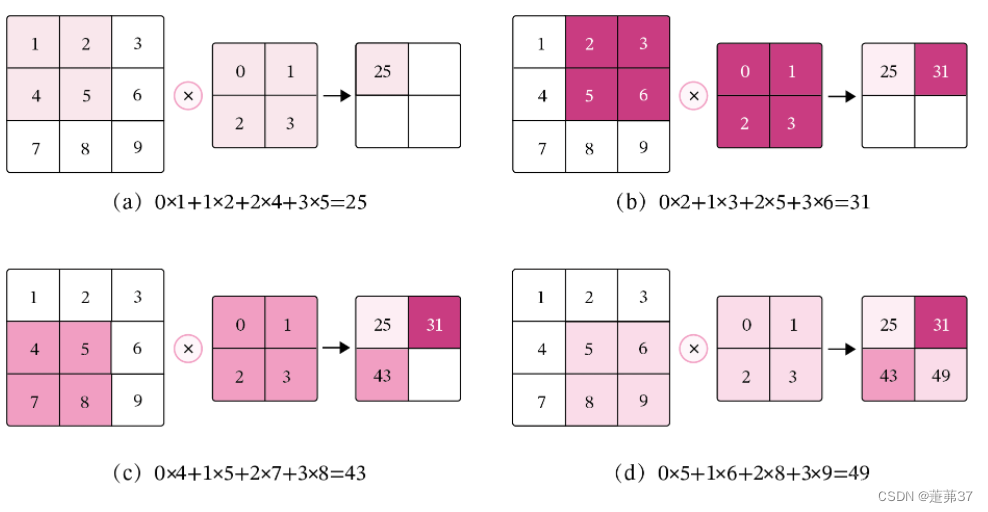
# 1. 主成分分析（PCA）概述

主成分分析（PCA）是一种经典的降维技术，广泛应用于数据分析和机器学习领域。PCA的目的是将高维数据投影到低维空间，同时最大程度地保留数据的方差。

PCA的原理基于正交性原理和方差最大化原理。正交性原理确保投影后的数据在低维空间中相互正交，从而避免信息重叠。方差最大化原理则保证投影后的数据具有最大的方差，即包含了原始数据中最多的信息。

# 2. PCA的正交性原理

### 2.1 正交基的概念和性质

**正交基**是一组向量，它们相互垂直，即它们的内积为0。在n维空间中，一组正交基可以表示为：

v_1, v_2, ..., v_n

其中，任意两个向量的内积为：

v_i · v_j = 0,  i ≠ j

正交基具有以下性质：

* **线性无关：**正交基中的向量线性无关，即它们不能由其他向量线性组合得到。
* **单位长度：**正交基中的向量通常被归一化，即它们的长度为1。
* **完备性：**正交基可以张成整个n维空间，即任何n维向量都可以表示为正交基向量的线性组合。

### 2.2 PCA正交化的数学推导

PCA的正交化过程可以数学上表示为：

X = UΣV^T

其中：

* X 是原始数据矩阵
* U 是正交特征向量矩阵
* Σ 是特征值对角矩阵
* V^T 是正交特征向量矩阵的转置

正交化过程的目的是将原始数据矩阵X投影到特征向量构成的子空间中，从而得到降维后的数据。

### 2.3 正交性在PCA降维中的作用

正交性在PCA降维中起着至关重要的作用：

* **保证降维后的数据是正交的：**正交特征向量构成的子空间是正交的，因此投影到该子空间中的数据也是正交的。
* **最大化方差：**正交化过程最大化了投影数据的方差，从而保留了原始数据中最重要的信息。
* **减少冗余信息：**正交性消除了数据中的冗余信息，使降维后的数据更加紧凑和有效。

**代码块：**

import numpy as np

# 原始数据矩阵
X = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# 计算正交特征向量和特征值
U, s, Vh = np.linalg.svd(X)

# 降维后的数据
X_reduced = np.dot(X, U[:, :2])

# 验证正交性
print(np.dot(X_reduced[:, 0], X_reduced[:, 1]))  # 0

**逻辑分析：**

该代码块演示了PCA正交化的过程。它使用奇异值分解（SVD）计算原始数据矩阵X的正交特征向量和特征值。然后，它将X投影到前两个特征向量构成的子空间中，得到降维后的数据X_reduced。最后，它验证了降维后数据的正交性，结果为0，表明数据是正交的。

# 3.1 方差的概念和意义

**方差**是衡量随机变量离散程度的度量，它表示随机变量与其期望值之间的平均偏差平方。对于一个随机变量 X，其方差定义为：

Var(X) = E[(X - E[X])^2]

其中，E[X] 表示 X 的期望值。

方差具有以下性质：

* **非负性：**方差总是大于或等于 0。
* **加性：**如果 X 和 Y 是两个独立的随机变量，则 Var(X + Y) = Var(X) + Var(Y)。
* **标度不变性：**如果 X 是一个随机变量，c 是一个常数，则 Var(cX) = c^2 * Var(X)。

### 3.2 PCA方差最大化的数学推导

PCA 的目标是找到一组正交单位向量，使得数据在这些向量上的投影具有最大的方差。数学上，可以将 PCA 方差最大化的过程表述为一个优化问题：

max  Var(W^T X)
s.t. W^T W = I

其中，X 是数据矩阵，W 是投影矩阵，I 是单位矩阵。

这个优化问题的拉格朗日函数为：

L(W, \lambda) = Var(W^T X) - \lambda(W^T W - I)

其中，λ 是拉格朗日乘子。

对 W 求偏导并令其为 0，得到：

\frac{\partial L}{\partial W} = 2X(X^T W) - 2\lambda W = 0

化简后得到：

X^T X W = \lambda W

这意味着 W 是 X^T X 的特征向量。由于 X^T X 是一个协