主成分分析（PCA）在金融领域的应用：风险评估与投资组合优化，一文看懂

# 1. 主成分分析（PCA）简介

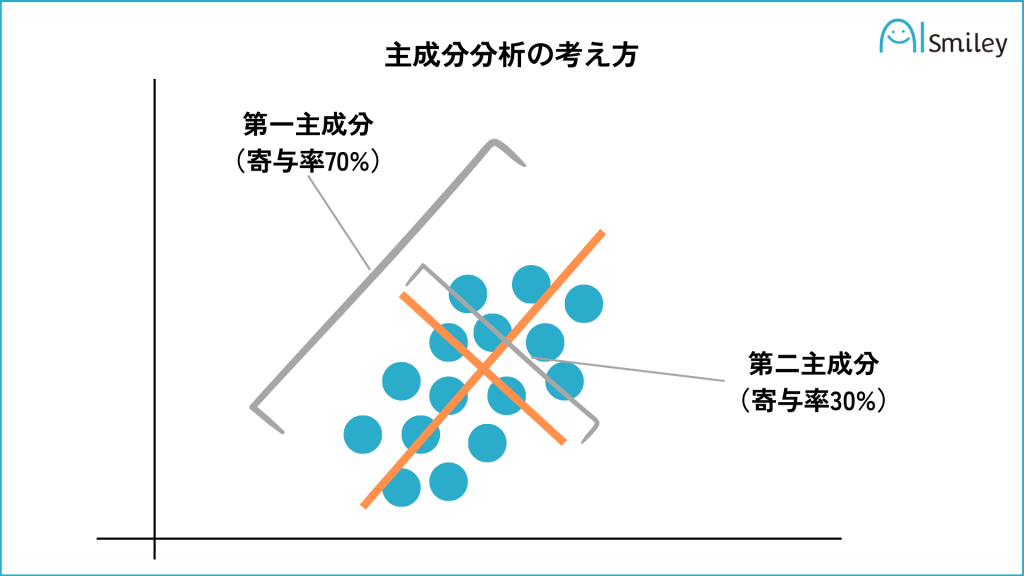
主成分分析（PCA）是一种统计降维技术，用于识别和提取数据集中的主要模式和趋势。它通过将原始变量线性组合成一组新的正交变量（主成分）来实现降维，这些主成分捕获了原始数据中最大的方差。

PCA在金融领域有着广泛的应用，因为它可以有效地减少金融数据的维度，同时保留其最重要的特征。这对于理解金融数据的复杂性、识别风险因素和构建预测模型至关重要。

# 2. PCA在金融领域的理论基础

### 2.1 PCA的数学原理和算法

**数学原理**

PCA是一种线性变换，将原始数据映射到一个新的正交坐标系中，使得新坐标系中的前几个主成分包含了原始数据的大部分方差。

设X为n×p的原始数据矩阵，其中n为样本数，p为特征数。PCA的目标是找到一个p×p的正交矩阵P，使得：

Y = XP

其中，Y为n×p的转换后的数据矩阵，每一列代表一个主成分。

**算法**

PCA的算法步骤如下：

1. 对原始数据进行中心化，即减去每一列的均值。
2. 计算协方差矩阵C = XX'。
3. 计算协方差矩阵C的特征值和特征向量。
4. 将特征值按从大到小排序，取前k个特征值对应的特征向量，构成正交矩阵P。
5. 将原始数据X与P相乘，得到转换后的数据Y。

### 2.2 PCA在金融数据的降维和特征提取中的应用

**降维**

PCA可以有效地对金融数据进行降维，减少特征数量，同时保留数据的关键信息。例如，对于一个股票市场数据集，PCA可以将数百个股票特征降维到几个主成分，这些主成分代表了市场的主要趋势。

**特征提取**

PCA还可以提取金融数据的关键特征，这些特征可以用于进一步的分析和建模。例如，PCA可以提取债券市场数据的收益率曲线，该曲线反映了不同期限债券的收益率关系。

**代码示例**

import numpy as np
from sklearn.decomposition import PCA

# 原始数据
X = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# PCA降维
pca = PCA(n_components=2)
pca.fit(X)

# 转换后的数据
Y = pca.transform(X)

# 打印主成分
print(pca.components_)

**逻辑分析**

该代码演示了如何使用PCA对金融数据进行降维。`PCA`类使用`fit`方法计算协方差矩阵并提取主成分。`transform`方法将原始数据转换为新的正交坐标系，其中前两个主成分包含了原始数据的大部分方差。

# 3.1 PCA用于识别金融风险因素

### 3.1.1 风险因素的识别原则

在金融风险评估中，风险因素的识别是至关重要的。PCA作为一种降维和特征提取技术，可以有效地从高维金融数据中识别出主要的风险因素。

识别风险因素的原则主要包括：

- **相关性：**风险因素应与金融资产的收益率或风险指标高度相关。
- **代表性：**风险因素应代表金融市场中主要的风险来源，如市场风险、利率风险、信用风险等