【K均值聚类算法实战手册】：掌握算法原理，轻松应对数据聚类挑战

# 1. K均值聚类算法概述**

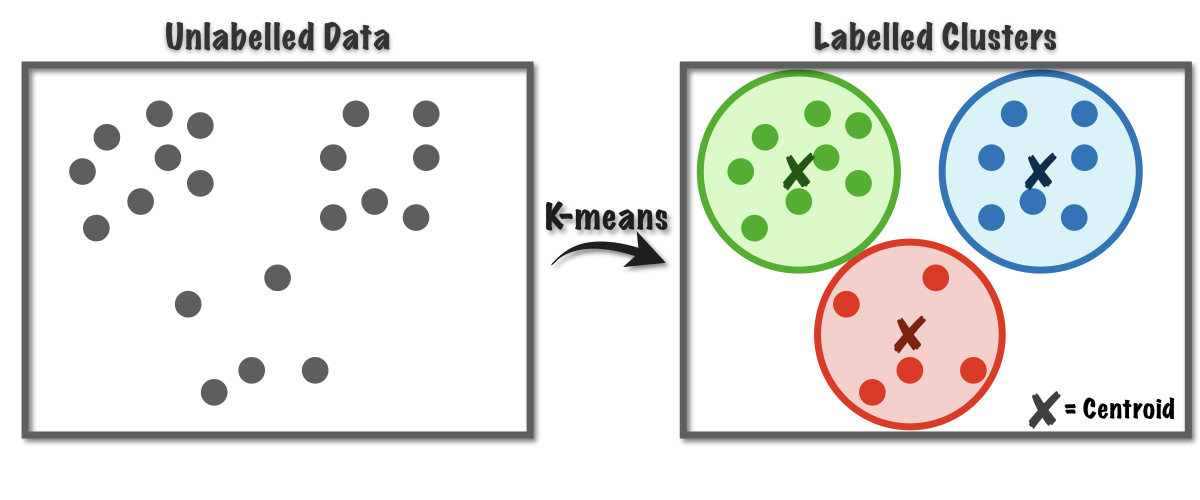
K均值聚类算法是一种无监督机器学习算法，用于将数据点划分为一组不同的簇。其目标是找到一组簇中心点，使每个数据点到其最近簇中心点的距离之和最小。K均值算法简单易用，广泛应用于数据挖掘、图像处理和自然语言处理等领域。

K均值算法的原理是：首先随机选择K个簇中心点，然后将每个数据点分配到距离最近的簇中心点。接下来，更新簇中心点为该簇中所有数据点的平均值。重复此过程，直到簇中心点不再发生变化或达到最大迭代次数。

# 2. K均值聚类算法理论基础

### 2.1 K均值聚类算法的原理和步骤

K均值聚类算法是一种无监督学习算法，用于将数据点划分为K个簇。算法的原理是：

1. **随机初始化：**随机选择K个数据点作为初始簇中心。
2. **分配数据点：**将每个数据点分配到距离其最近的簇中心所在的簇中。
3. **更新簇中心：**计算每个簇中所有数据点的平均值，并将其作为新的簇中心。
4. **重复步骤2和3：**重复步骤2和3，直到簇中心不再发生变化，或达到最大迭代次数。

### 2.2 K值的确定方法

K值的确定是K均值聚类算法中的一个关键问题。K值过小会导致簇数不足，无法充分反映数据的分布；K值过大会导致簇数过多，造成过度拟合。

确定K值的方法有：

- **肘部法：**绘制簇数与聚类误差之间的曲线，选择误差下降最快的点对应的簇数。
- **轮廓系数：**计算每个数据点与所属簇和邻近簇之间的相似度，选择轮廓系数最高的簇数。
- **交叉验证：**将数据集划分为多个子集，对每个子集进行聚类，选择在所有子集上平均误差最小的簇数。

### 2.3 距离度量和相似性计算

K均值聚类算法中，数据点之间的距离度量是至关重要的。常用的距离度量包括：

- **欧氏距离：**计算两个数据点之间坐标差的平方和的平方根。
- **曼哈顿距离：**计算两个数据点之间坐标差的绝对值之和。
- **余弦相似度：**计算两个数据点之间向量夹角的余弦值。

相似性计算是距离度量的逆过程，常用的相似性计算方法包括：

- **皮尔逊相关系数：**计算两个数据点之间协方差与标准差的比值。
- **余弦相似度：**计算两个数据点之间向量夹角的余弦值。
- **杰卡德相似度：**计算两个集合之间交集元素个数与并集元素个数的比值。

# 3.1 Python中K均值聚类算法的实现

#### 3.1.1 导入必要的库

import numpy as np
import pandas as pd
from sklearn.cluster import KMeans

**参数说明：**

* `numpy`: 用于数学和科学计算。
* `pandas`: 用于数据处理和分析。
* `sklearn.cluster.KMeans`: 提供了K均值聚类算法的实现。

#### 3.1.2 数据预处理

数据预处理是聚类算法的重要步骤，它可以提高算法的准确性和效率。对于K均值聚类算法，数据预处理通常包括：

* **数据标准化或归一化：**将数据缩放至相同范围，以避免某些特征对聚类结果产生过大影响。
* **缺失值处理：**删除缺失值或使用插值方法填充缺失值。
* **异常值处理：**识别并删除异常值，因为它们可能会扭曲聚类结果。

#### 3.1.3 算法步骤实现

# 创建KMeans对象
kmeans = KMeans(n_clusters=3, init='k-means++', max_iter=300)

# 拟合数据
kmeans.fit(data)

# 获取聚类标签
labels = kmeans.labels_

# 获取聚类中心
centroids = kmeans.cluster_centers_

**逻辑分析：**

* `KMeans(n_clusters=3, init='k-means++', max_iter=300)`：创建KMeans对象，指定聚类数为3，使用K均值++算法初始化中心，并设置最大迭代次数为300。
* `kmeans.fit(data)`：将数据拟合到KMeans模型中，执行聚类算法。
* `kmeans.labels_`：获取每个数据点的聚类标签。
* `kmeans.cluster_centers_`：获取聚类中心。

### 3.2 其他语言中K均值聚类算法的实现

K均值聚类算法在其他编程语言中也有广泛的实现，例如：

* **Java：**可以使用`weka.clusterers.SimpleKMeans`类。
* **R：**可以使用`kmeans()`函数。
* **C++：**可以使用`mlpack::kmeans`库。

# 4. K均值聚类算法应用案例

### 4.1 文本聚类

#### 4.1.1 文本预处理

文本聚类在文本挖掘和自然语言处理中广泛应用。在文本聚类之前，需要对文本进行预处理，包括：

- **分词：**将文本分割成一个个词语。
- **去停用词：**去除一些常见的无意义词语，如“的”、“是”、“了”等。
- **词干提取：**将词语还原为其基本形式，如“running”还原为“run”。

#### 4.1.2 文本特征提取

文本预处理后，需要提取文本特征。常用的文本特征提取方法有：

- **词频-逆向文件频率（TF-IDF）：**计算每个词语在文本中出现的频率，并根据其在所有文本中出现的频率进行加权。
- **词嵌入：**将词语映射到一个高维向量空间，每个维度代表词语的语义特征。

#### 4.1.3 聚类结果分析

文本聚类后，需要对聚类结果进行分析，包括：

- **聚类质量评估：**使用指标如轮廓系数、Calinski-Harabasz指数等评估聚类质量。
- **聚类标签解释：**分析每个聚类中包含的文本，并为其分配一个标签。
- **聚类可视化：**使用散点图、树状图等可视化技术展示聚类结果。

### 4.2 图像聚类

#### 4.2.1 图像特征提取

图像聚类在图像处理和计算机视觉中应用广泛。在图像聚类之前，需要提取图像特征。常用的图像特征提取方法有：

- **颜色直方图：**计算图像中每个颜色通道的频率分布。
- **纹理特征：**提取图像中的纹理信息，如灰度共生矩阵、局部二值模式等。
- **形状特征：**提取图像中的形状信息，如轮廓、面积、周长等。

#### 4.2.2 聚类结果可视化

图像聚类后，需要对聚类结果进行可视化，包括：

- **聚类图像展示：**将聚类后的图像展示出来，并标注其聚类标签。
- **聚类中心展示：**展示每个聚类的中心图像，代表该聚类的特征。
- **聚类分布可视化：**使用散点图、热图等可视化技术展示聚类结果的分布情况。

# 5. K均值聚类算法进阶应用

### 5.1 K均值++算法

K均值++算法是一种初始化K均值聚类算法中心点的改进算法。它通过一种概率选择的方式来选择中心点，可以有效地避免随机选择中心点导致的局部最优问题。

**算法步骤：**

1. 随机选择一个点作为第一个中心点。
2. 对于每个剩余的点，计算它与已选中心点的距离。
3. 将每个点被选为下一个中心点的概率设置为其距离的平方。
4. 根据概率分布随机选择下一个中心点。
5. 重复步骤2-4，直到选择出K个中心点。

### 5.2 流式K均值聚类算法

流式K均值聚类算法是一种在线聚类算法，可以处理不断流入的数据。它通过维护一个聚类模型，并在新数据到来时更新模型来实现。

**算法步骤：**

1. 初始化一个聚类模型，包括K个中心点。
2. 当新数据到来时，计算它与每个中心点的距离。
3. 将新数据分配到距离最近的中心点所在的簇。
4. 更新中心点的位置，使其为簇中所有点的平均值。

### 5.3 层次K均值聚类算法

层次K均值聚类算法是一种分层聚类算法，它通过逐步分割数据来构建一个层次结构的聚类模型。

**算法步骤：**

1. 将所有数据作为一个簇。
2. 对当前簇进行K均值聚类，得到K个子簇。
3. 重复步骤2，直到达到预定的层次深度或满足停止条件。

层次K均值聚类算法可以生成一个聚类树，其中每个节点表示一个簇，叶子节点表示最终的聚类结果。