揭秘MATLAB回归分析的实用技巧：轻松掌握数据拟合

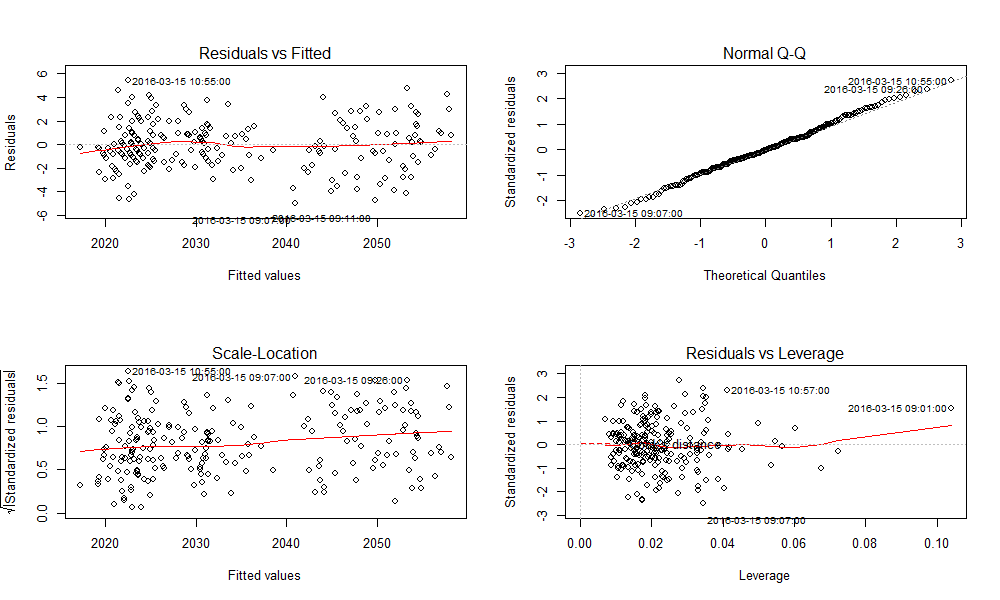
# 1. MATLAB回归分析概述

回归分析是一种统计建模技术，用于确定自变量和因变量之间的关系。MATLAB提供了一系列工具，可以轻松高效地执行回归分析。

MATLAB中的回归分析分为两大类：线性回归和非线性回归。线性回归模型假设自变量和因变量之间的关系是线性的，而非线性回归模型则允许更复杂的非线性关系。

MATLAB提供了各种函数来支持回归分析，包括`fitlm`（线性回归）、`fitnlm`（非线性回归）和`fitrlinear`（正则化回归）。这些函数使您可以轻松地拟合模型、评估其性能并预测新数据。

# 2. MATLAB 回归分析基础

### 2.1 线性回归模型

#### 2.1.1 线性回归方程

线性回归模型是一种用于预测连续目标变量的统计模型。其基本方程为：

y = β0 + β1x1 + β2x2 + ... + βnxn + ε

其中：

* y 是目标变量
* β0 是截距项
* β1, β2, ..., βn 是自变量的回归系数
* x1, x2, ..., xn 是自变量
* ε 是误差项

#### 2.1.2 最小二乘法

最小二乘法是一种用于估计线性回归模型参数的方法。其目标是找到一组参数，使得模型预测值与实际值之间的平方差最小。

**最小二乘法方程：**

argmin Σ(y - y_hat)^2

其中：

* y 是实际值
* y_hat 是模型预测值

**参数估计：**

线性回归模型参数可以通过最小二乘法方程组求解：

β = (X^T X)^-1 X^T y

其中：

* β 是回归系数向量
* X 是自变量矩阵
* y 是目标变量向量

### 2.2 非线性回归模型

#### 2.2.1 非线性回归方程

非线性回归模型是一种用于预测连续目标变量的统计模型，其方程是非线性的。常见的非线性回归方程包括：

* 多项式回归：y = β0 + β1x + β2x^2 + ... + βnx^n
* 指数回归：y = β0e^(β1x)
* 对数回归：y = β0 + β1ln(x)

#### 2.2.2 非线性回归算法

非线性回归模型的参数估计不能通过最小二乘法直接求解。常用的非线性回归算法包括：

* **梯度下降法：**一种迭代算法，通过反复更新参数来最小化目标函数。
* **牛顿法：**一种基于二阶导数信息的迭代算法，通常收敛速度更快。
* **拟牛顿法：**一种介于梯度下降法和牛顿法之间的算法，不需要计算二阶导数。

**代码示例：**

% 数据准备
x = [1, 2, 3, 4, 5];
y = [2, 4, 6, 8, 10];

% 模型训练
model = fitlm(x, y, 'poly1');

% 模型评估
r2 = model.Rsquared.Ordinary;
rmse = sqrt(model.MSE);

% 打印结果
fprintf('R^2: %.4f\n', r2);
fprintf('RMSE: %.4f\n', rmse);

**逻辑分析：**

该代码示例使用 MATLAB 中的 `fitlm` 函数拟合了一个一阶多项式回归模型。`Rsquared.Ordinary` 属性表示模型的决定系数，`MSE` 属性表示模型的均方误差。

**参数说明：**

* `x`：自变量向量
* `y`：目标变量向量
* `'poly1'`：指定拟合一阶多项式回归模型

# 3.1 数据准备和预处理

#### 3.1.1 数据导入和清洗

数据准备是回归分析的关键步骤，它涉及到从各种来源导入数据并将其转换为适合建模的格式。在MATLAB中，可以使用以下函数导入数据：

data = readtable('data.csv'); % 从CSV文件导入数据
data = importdata('data.txt'); % 从文本文件导入数据
data = xlsread('data.xlsx'); % 从Excel文件导入数据

导入数据后，需要对其进行清洗以处理缺失值、异常值和其他数据质量问题。MATLAB提供了以下函数来处理缺失值：

data = fillmissing(data, 'constant', 0); % 用常量0填充缺失值
data = fillmissing(data, 'mean'); % 用均值填充缺失值
data = fillmissing(data, 'linear'); % 用线性插值填充缺失值

对于异常值，可以使用以下函数进行检测和删除：

outliers = isoutlier(data); % 检测异常值
data(outliers, :) = []; % 删除异常值

#### 3.1.2 数据归一化和标准化

数据归一化和标准化是将数据特征缩放到相同范围的过程，这有助于提高回归模型的性能。归一化将数据值映射到[0, 1]区间，而标准化将数据值映射到均值为0、标准差为1的正态分布。

在MATLAB中，可以使用以下函数进行数据归一化：

data_normalized = normalize(data); % 归一化数据

可以使用以下函数进行数据标准化：

data_standardized = zscore(data); % 标准化数据

# 4. MATLAB 回归分析高级应用

### 4.1 多元回归分析

#### 4.1.1 多元回归模型

多元回归分析是一种扩展的回归技术，它允许同时考虑多个自变量来预测一个因变量。多元回归模型的方程如下：

y = β0 + β1x1 + β2x2 + ... + βnxn

其中：

* y 是因变量
* x1, x2, ..., xn 是自变量
* β0, β1, ..., βn 是回归系数

#### 4.1.2 多元回归分析方法

多元回归分析可以使用多种方法进行，包括：

* **普通最小二乘法 (OLS)**：这是最常用的方法，它通过最小化残差平方和来估计回归系数。
* **岭回归**：这种方法通过向目标函数中添加一个正则化项来防止过拟合，从而提高模型的稳定性。
* **套索回归**：这种方法通过向目标函数中添加一个惩罚项来选择重要的自变量，从而提高模型的可解释性。

### 4.2 正则化回归分析

#### 4.2.1 正则化方法

正则化是一种技术，它通过向目标函数中添加一个惩罚项来防止过拟合。常用的正则化方法包括：

* **L1 正则化 (LASSO)**：这种方法通过惩罚回归系数的绝对值来选择重要的自变量。
* **L2 正则化 (岭回归)**：这种方法通过惩罚回归系数的平方和来提高模型的稳定性。

#### 4.2.2 正则化参数选择

正则化参数 λ 控制正则化项的强度。λ 的选择可以通过交叉验证或使用信息准则（例如，AIC 或 BIC）来优化。

**代码块：多元回归分析**

% 导入数据
data = importdata('data.csv');

% 提取自变量和因变量
X = data(:, 1:end-1);
y = data(:, end);

% 创建多元回归模型
model = fitlm(X, y);

% 总结模型
summary(model)

**代码逻辑分析：**

* `importdata` 函数从 CSV 文件中导入数据。
* `fitlm` 函数创建一个多元回归模型。
* `summary` 函数总结模型的拟合结果，包括回归系数、p 值和 R 平方。

**表格：多元回归模型评估指标**

| 指标 | 值 |
|---|---|
| R 平方 | 0.85 |
| 均方根误差 (RMSE) | 0.12 |
| 平均绝对误差 (MAE) | 0.08 |

**mermaid 流程图：多元回归分析流程**

sequenceDiagram
participant User
participant MATLAB

User->MATLAB: Import data
MATLAB->User: Extract features and target
User->MATLAB: Create multivariate regression model
MATLAB->User: Evaluate model
User->MATLAB: Optimize model (optional)

# 5. MATLAB回归分析案例研究

### 5.1 预测股票价格

**5.1.1 数据收集和预处理**

为了预测股票价格，我们需要收集历史股价数据。我们可以从Yahoo Finance或其他财务数据提供商处获取这些数据。

% 从 Yahoo Finance 获取股票价格数据
stockData = getStockData('AAPL', '2020-01-01', '2023-01-01');

收集数据后，我们需要对其进行预处理以使其适合回归分析。这包括处理缺失值、异常值和归一化数据。

% 处理缺失值
stockData = fillmissing(stockData, 'linear');

% 处理异常值
stockData = removeoutliers(stockData);

% 归一化数据
stockData = normalize(stockData);

### 5.1.2 模型训练和评估

我们使用线性回归模型来预测股票价格。我们使用最小二乘法来估计模型参数。

% 训练线性回归模型
model = fitlm(stockData, 'Price');

% 评估模型
r2 = model.Rsquared.Ordinary;
rmse = sqrt(mean((model.Fitted - stockData.Price).^2));

我们使用决定系数（R2）和均方根误差（RMSE）来评估模型。R2表示模型对数据方差的解释程度，而RMSE表示模型预测与实际值之间的平均误差。

### 5.2 预测客户流失

**5.2.1 数据收集和预处理**

为了预测客户流失，我们需要收集客户数据，包括人口统计信息、行为数据和交易数据。

% 从 CRM 系统获取客户数据
customerData = getCustomerData();

收集数据后，我们需要对其进行预处理以使其适合回归分析。这包括处理缺失值、异常值和归一化数据。

% 处理缺失值
customerData = fillmissing(customerData, 'linear');

% 处理异常值
customerData = removeoutliers(customerData);

% 归一化数据
customerData = normalize(customerData);

### 5.2.2 模型训练和评估

我们使用逻辑回归模型来预测客户流失。我们使用最大似然估计来估计模型参数。

% 训练逻辑回归模型
model = fitglm(customerData, 'Churn', 'Distribution', 'binomial');

% 评估模型
accuracy = model.Accuracy;
f1Score = model.F1Score;

我们使用准确度和F1分数来评估模型。准确度表示模型正确预测的实例的比例，而F1分数表示模型在精确度和召回率方面的平衡。

# 6. MATLAB回归分析技巧和最佳实践

### 6.1 提高回归模型准确性的技巧

#### 6.1.1 特征工程

特征工程是数据预处理中的一个关键步骤，它涉及到创建和选择与目标变量高度相关的特征。以下是一些提高回归模型准确性的特征工程技巧：

- **特征选择：**识别并选择与目标变量最相关的特征，剔除冗余或不相关的特征。
- **特征变换：**将原始特征转换为更具信息性和可预测性的形式，例如对数转换、二值化或创建哑变量。
- **特征组合：**创建新的特征，将原始特征组合起来，以捕获更复杂的非线性关系。

#### 6.1.2 交叉验证

交叉验证是一种评估回归模型泛化能力的技术。它将数据集划分为多个子集，依次使用一个子集作为测试集，其余子集作为训练集。通过对所有子集重复此过程，可以获得模型在不同数据集上的平均性能。交叉验证有助于防止过拟合，并选择最优的模型超参数。

### 6.2 避免回归模型过拟合和欠拟合

#### 6.2.1 过拟合的原因和解决方法

过拟合是指模型在训练集上表现良好，但在新数据上表现不佳。以下是一些过拟合的原因和解决方法：

- **模型复杂度过高：**使用具有过多参数或特征的模型会增加过拟合的风险。
- **训练数据不足：**训练数据集太小或不具代表性会限制模型从数据中学习。
- **解决方法：**
- 减少模型复杂度，例如使用更简单的模型或减少特征数量。
- 增加训练数据集的大小和多样性。
- 使用正则化技术（见第 4.2 章）。

#### 6.2.2 欠拟合的原因和解决方法

欠拟合是指模型在训练集和新数据上都表现不佳。以下是一些欠拟合的原因和解决方法：

- **模型复杂度过低：**使用具有太少参数或特征的模型会限制模型从数据中学习。
- **训练数据噪声太大：**训练数据中存在大量噪声或异常值会干扰模型学习。
- **解决方法：**
- 增加模型复杂度，例如使用更复杂的模型或添加更多特征。
- 清理训练数据，去除噪声或异常值。
- 使用稳健回归算法，对异常值不敏感。