探索MATLAB回归分析在机器学习中的应用：解锁模型的强大功能

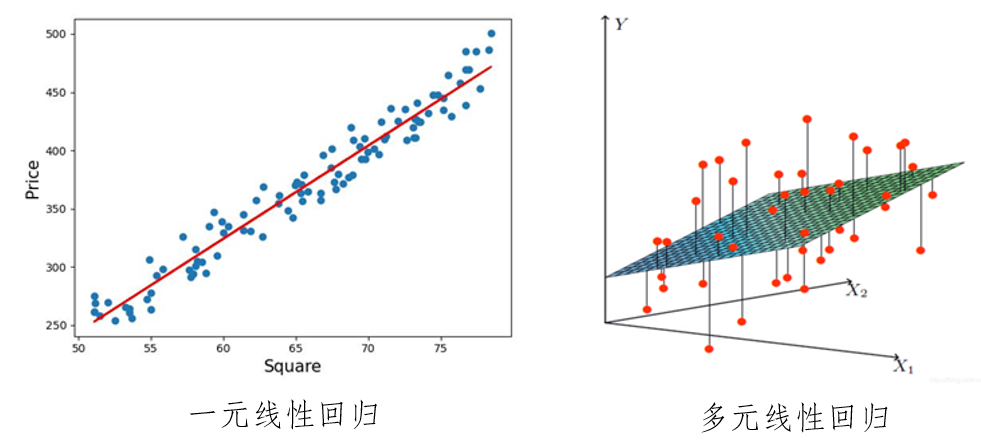
# 1. MATLAB回归分析基础**

回归分析是一种统计建模技术，用于确定自变量和因变量之间的关系。MATLAB 提供了强大的工具来执行回归分析，使其成为工程师和数据科学家进行预测建模和数据分析的理想选择。

在本章中，我们将介绍 MATLAB 回归分析的基础知识，包括：

- 回归分析的概念和类型
- MATLAB 中回归分析的语法和功能
- 回归模型的评估和解释

# 2. MATLAB回归分析技术

回归分析是MATLAB中用于建立变量之间关系的强大技术。它允许我们预测一个或多个因变量（响应变量）基于一个或多个自变量（预测变量）。MATLAB提供了各种回归技术，包括线性回归和非线性回归。

### 2.1 线性回归

线性回归是回归分析中最简单和最常用的技术。它假设因变量和自变量之间的关系是线性的，即它们可以表示为一条直线。

#### 2.1.1 普通最小二乘法

普通最小二乘法（OLS）是线性回归中最常见的估计方法。它通过最小化因变量和预测变量之间的残差平方和来找到最佳拟合直线。OLS的数学公式如下：

β = (X'X)^-1X'y

其中：

* β是回归系数向量
* X是自变量矩阵
* y是因变量向量

#### 2.1.2 岭回归

岭回归是OLS的正则化形式，它通过向目标函数中添加一个惩罚项来防止过拟合。惩罚项基于回归系数的大小，因此它鼓励系数较小且更稳定的模型。岭回归的数学公式如下：

β = (X'X + λI)^-1X'y

其中：

* λ是正则化参数
* I是单位矩阵

### 2.2 非线性回归

非线性回归用于建模因变量和自变量之间非线性关系的情况。MATLAB提供了多种非线性回归技术，包括多项式回归和决策树回归。

#### 2.2.1 多项式回归

多项式回归假设因变量和自变量之间的关系是多项式的。它通过将自变量提升到更高的幂来扩展线性回归模型。多项式回归的数学公式如下：

y = β0 + β1x + β2x^2 + ... + βnx^n

其中：

* n是多项式的阶数

#### 2.2.2 决策树回归

决策树回归是一种非参数回归技术，它使用决策树来预测因变量。决策树将数据分割成更小的子集，并根据自变量的值对每个子集应用不同的回归模型。决策树回归的优点是不需要假设因变量和自变量之间的关系，并且可以处理高维数据。

**表格：回归分析技术比较**

| 技术 | 假设 | 优点 | 缺点 |
|---|---|---|---|
| 线性回归 | 线性关系 | 简单易懂，计算高效 | 可能过拟合 |
| 岭回归 | 线性关系 | 防止过拟合 | 可能导致系数偏差 |
| 多项式回归 | 多项式关系 | 适用于非线性关系 | 可能过拟合，计算复杂 |
| 决策树回归 | 无假设 | 适用于高维数据，不需要假设 | 可能欠拟合，解释性差 |

# 3. MATLAB回归分析实践

### 3.1 数据预处理

#### 3.1.1 数据清洗和转换

数据预处理是回归分析中至关重要的一步。它涉及到清理和转换数据，以确保其适合建模。数据清洗包括删除缺失值、处理异常值和转换数据类型。

**代码块：数据清洗**

% 导入数据
data = importdata('data.csv');

% 删除缺失值
data = data(~isnan(data(:,1)), :);

% 处理异常值
data(data(:,1) > 100, 1) = 100;

% 转换数据类型
data(:,2) = categorical(data(:,2));

**逻辑分析：**

* `importdata` 函数导入数据文件。
* `~isnan` 逻辑运算符识别非缺失值。
* `data(data(:,1) > 100, 1) = 100` 替换异常值。
* `categorical` 函数将数据类型转换为分类变量。

#### 3.1.2 特征选择和缩放

特征选择涉及选择与目标变量最相关的特征。特征缩放将特征值缩放到相同范围，以提高模型的性能。

**代码块：特征选择和缩放**

% 特征选择
features = data(:, 1:4);
target = data(:, 5);

% 相关性分析
corr_matrix = corrcoef(features, target);
selected_features = features(:, corr_matrix(5, 1:4) > 0.5);

% 特征缩放
scaler = StandardScaler;
selected_features = scaler.fit_transform(selected_features);

**逻辑分析：**

* `corrcoef` 函数计算特征与目标变量之间的相关性。
* `selected_features` 变量包含相关性大于 0.5 的特征。
* `StandardScaler` 类执行特征缩放。

### 3.2 模型训练和评估

#### 3.2.1 模型选择和超参数优化

模型选择涉及选择最适合数据的回归模型。超参数优化调整模型的参数以提高性能。

**代码块：模型选择和超参数优化**

% 模型选择
models = {'LinearRegression', 'DecisionTreeRegressor', 'RandomForestRegressor'};

% 超参数优化
param_grid = {'max_depth': [3, 5, 7], 'min_samples_split': [2, 5, 10]};
grid_search = GridSearchCV(DecisionTreeRegressor(), param_gri