Segment Trees
Motivational Problems:
http://www.spoj.pl/problems/BRCKTS/
http://www.spoj.com/problems/GSS3/
http://www.spoj.com/problems/HORRIBLE
http://www.spoj.pl/problems/IOPC1207/
https://www.spoj.com/problems/GSS2/
http://www.spoj.com/problems/SEGSQRSS/
http://www.spoj.com/problems/ORDERSET/
http://www.spoj.com/problems/HELPR2D2/
http://www.spoj.com/problems/TEMPLEQ
Segment trees (shortened as segtrees), as some of you might have heard of, is a cool data structure, primarily used for range queries. It is a
height balanced binary tree with a static structure. The nodes of segment tree correspond to various intervals, and can be augmented with
appropriate information pertaining to those intervals. It is somewhat less powerful than balanced binary trees because of its static structure, but
due to the recursive nature of operations on the segtree, it is incredibly easy to think about and code.
Structure
In a segtree, the basic structure (an array in almost all cases) on which you want to answer queries are stored at leaves of the tree, in the
sequential order. All internal nodes is formed by "merging" its left and right children. The overall tree is a complete binary tree of height n.
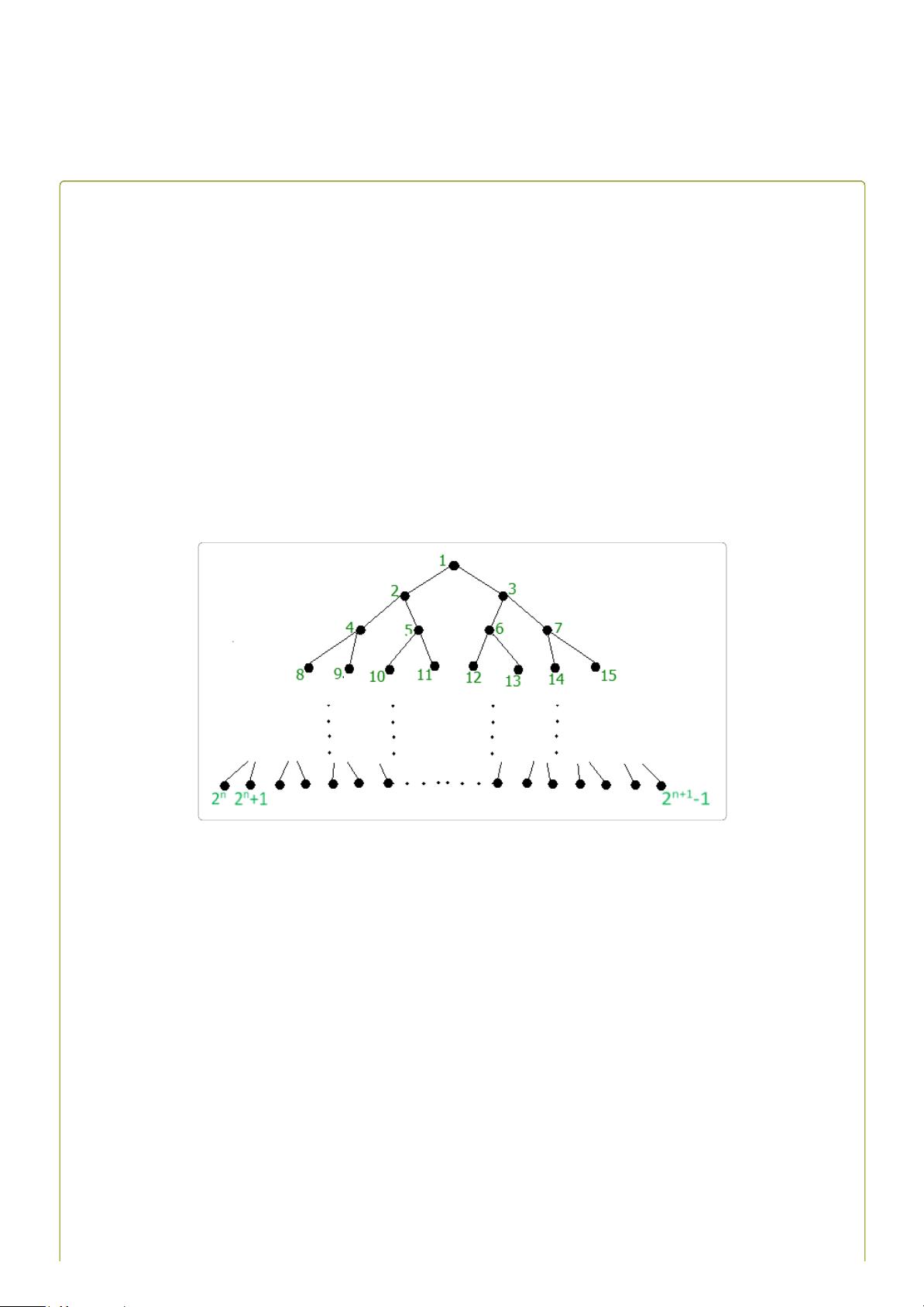
The diagram shows how the binary tree is built up and how the nodes are indexed. Given a node with label i, its left and right children are 2i and
2i+1 respectively, and nodes i*2
k
to (i+1)*2
k
-1 are its kth level descendants. However, segtrees are most effective when you think of them as just a
recursive structure.
As an example, consider a segment tree with n=3. As in the above figure, this would mean that the segment tree has 15 nodes. Such a segment
tree could be used to store ranges corresponding to an array of size 8 (indices 0 through 7). The leaf nodes (8 to 15) all correspond to intervals
containing one element only : That is, node 8 would correspond to the interval [0,0] in the array and node 9 would be [1,1] and so on. As we go up
the segtree, the interval corresponding to each node in the segtree is found by merging the intervals of its two children. That way, node 4 will
correspond to interval [0,1] and node 3 to interval [4,7] and so on.
Now assume that you need to make a query on some arbitrary interval in the array. The most straightforward way would be to look at the
lowermost level in the segment tree. But that would require as many operations as there are elements in the interval, and is hence costly. For
example, If one desires to query the interval [2,7], this would mean having to look at the nodes 10, 11, 12, 13, 14 and 15 in the segtree. But we
can be smart and choose only nodes 3 and 5 : the former takes care of the interval [4,7] while the latter takes care of [2,3]. When we have longer
intervals and thus deeper segtrees, the advantage gained by choosing conjoined intervals is huge. The basic idea behind segment trees is to
recursively choose the best intervals for updation and querying such that the total number of operations needed is reduced.
The exact implementation is detailed in the rest of the article. In this blog, I go on to show that most of the times, a segtree can be described by
these fundamental operations: merge, split and update_single_subtree. Add to it binary_search, and almost every variant of segtree that I have
come across can be broken down in terms of these operations. At the end of this blog, I will give a stl-like packaged version of segtree.
Basic Idea:
A segtree can be seen of as doing two things at the same time: a) The internal nodes summarize the information stored at descendant
A segtree on 2
n
elements. The children of node labelled i are (2*i) and (2*i+1).