贝叶斯统计方法基础教程

需积分: 0 179 浏览量更新于2024-06-21 收藏 2.82MB PDF 举报

"A First Course in Bayesian Statistical Methods" 是一本由Peter D. Hoff编著的统计学教材，专注于介绍贝叶斯统计学的基础概念和实践应用。该书源于华盛顿大学的研究生课程，适合已完成研究生级别统计入门课程并对此领域感兴趣的非统计学研究生，以及统计学一年级和二年级的学生学习。它提供了一个独立且紧凑的贝叶斯理论和实践介绍，旨在让读者能够理解和应用基本的贝叶斯统计方法进行数据分析。贝叶斯统计是一种统计推理方法，其中概率被解释为对未知参数的主观信念。在贝叶斯框架下，我们通过先验分布结合观测数据来更新我们的信念，得到后验分布。这种思想在许多科学领域都有应用，如医学研究、工程、社会科学和机器学习等。本书包含以下关键知识点： 1. **先验知识与后验分布**：解释了如何利用先验信息（通常是主观的或基于先前研究的信息）与观测数据结合，形成对未知参数的后验分布。书中可能会详细讨论贝叶斯定理及其在不同问题中的应用。 2. **贝叶斯模型**：涵盖了各种贝叶斯模型，如线性回归、逻辑回归、贝叶斯网络等，以及如何构建和选择合适的先验分布。 3. **计算方法**：由于贝叶斯模型通常涉及复杂的后验分布，因此会介绍蒙特卡洛方法，如马尔可夫链蒙特卡洛（MCMC）技术，如吉布斯采样和Metropolis-Hastings算法，这些方法用于近似后验分布。 4. **决策理论与贝叶斯分析**：可能讨论如何基于后验分布进行决策，包括贝叶斯决策规则和最小化风险。 5. **实证分析**：书中会包含实际案例研究，展示如何将理论应用于真实数据集，以解决具体问题。 6. **软件应用**：可能介绍R、WinBUGS、JAGS等软件，用于执行贝叶斯分析，帮助读者实现贝叶斯方法。 7. **批判性思考**：鼓励读者理解贝叶斯方法的优势（如能处理不确定性、提供完整的概率模型）和局限性（如对先验选择的敏感性）。通过阅读此书，读者将获得基础的贝叶斯统计工具箱，能够在自己的研究中运用贝叶斯方法。虽然不是为高级统计研究人员设计的全面手册，但本书可以作为他们快速了解贝叶斯方法的起点，为进一步深入研究打下基础。

1.2 Why Bayes? 7

people with weak prior beliefs (low values of w) or low prior expectations are

generally 90% or more certain that the infection rate is below 0.10. However,

a high degree of certainty (say 97.5%) is only achieved by people who already

thought the infection rate was lower than the average of the other cities.

Comparison to non-Bayesian methods

A standard estimate of a population proportion θ is the sample mean ¯y =

y/n, the fraction of infected people in the sample. For our sample in which

y = 0 this of course gives an estimate of zero, and so by using ¯y we would be

estimating that zero people in the city are infected. If we were to report this

estimate to a group of doctors or health oﬃcials we would probably want to

include the caveat that this estimate is subject to sampling uncertainty. One

way to describe the sampling uncertainty of an estimate is with a conﬁdence

interval. A popular 95% c onﬁdence interval for a population proportion θ is

the Wald interval, given by

¯y ±1.96

¯y(1 − ¯y)/n.

This interval has correct asymptotic frequentist coverage, meaning that if n

is large, then w ith probability approximately equal to 95%, Y will take on

a value y such that the above interval contains θ. Unfortunately this does

not hold for small n: For an n of around 20 the probability that the interval

contains θ is only about 80% (Agresti and Coull, 1998). Regardless, for our

sample in which ¯y = 0 the Wald conﬁdence interval comes out to be just a

single point: zero. In fact, the 99.99% Wald interval also comes out to be zero.

Certainly we would not want to conclude from the surve y that we are 99.99%

certain that no one in the city is infected.

People have suggested a variety of alternatives to the Wald interval in

hopes of avoiding this type of behavior. One type of conﬁdence interval that

performs well by non-Bayesian criteria is the “adjusted” Wald interval sug-

gested by Agresti and Coull (1998), which is given by

θ ± 1.96

θ(1 −

θ)/n , where

θ =

n + 4

¯y +

n + 4

While not originally motivated as such, this interval is clearly related to

Bayesian inference: The value of

θ here is equivalent to the posterior mean for

θ under a beta(2,2) prior distribution, which represents weak prior information

centered around θ = 1/2.

General estimation of a population mean

Given a random sample of n observations from a population, a standard es-

timate of the population mean θ is the sample mean ¯y. While ¯y is generally

professordoctordoron@gmail.com

8 1 Introduction and examples

a reliable e stimate for large sample sizes , as we saw in the example it can be

statistically unreliable for small n, in which case it serves more as a summary

of the sample data than as a precise estimate of θ.

If our interest lies more in obtaining an es timate of θ than in summarizing

our sample data, we may want to consider estimators of the form

θ =

n + w

¯y +

n + w

where θ

represents a “best guess” at the true value of θ and w represents a

degree of conﬁdence in the guess. If the sample size is large, then ¯y is a reliable

estimate of θ. The estimator

θ takes advantage of this by having its weights

on ¯y and θ

go to one and zero, respectively, as n increases. As a result, the

statistical properties of ¯y and

θ are essentially the same for large n. However,

for small n the variability of ¯y might be more than our uncertainty about θ

In this case, using

θ allows us to combine the data with prior information to

stabilize our estimation of θ.

These properties of

θ for both large and small n suggest that it is a useful

estimate of θ for a broad range of n. In Section 5.4 we will conﬁrm this by

showing that, under some conditions,

θ outperforms ¯y as an estimator of θ for

all values of n. As we saw in the infection rate example and will see again in

later chapters,

θ can be interpreted as a Bayesian estimator using a certain

class of prior distributions. Even if a particular prior distribution p(θ) does not

exactly reﬂect our prior information, the corresponding posterior distribution

p(θ|y) can still be a useful means of providing stable inference and estimation

for situations in which the sample size is low.

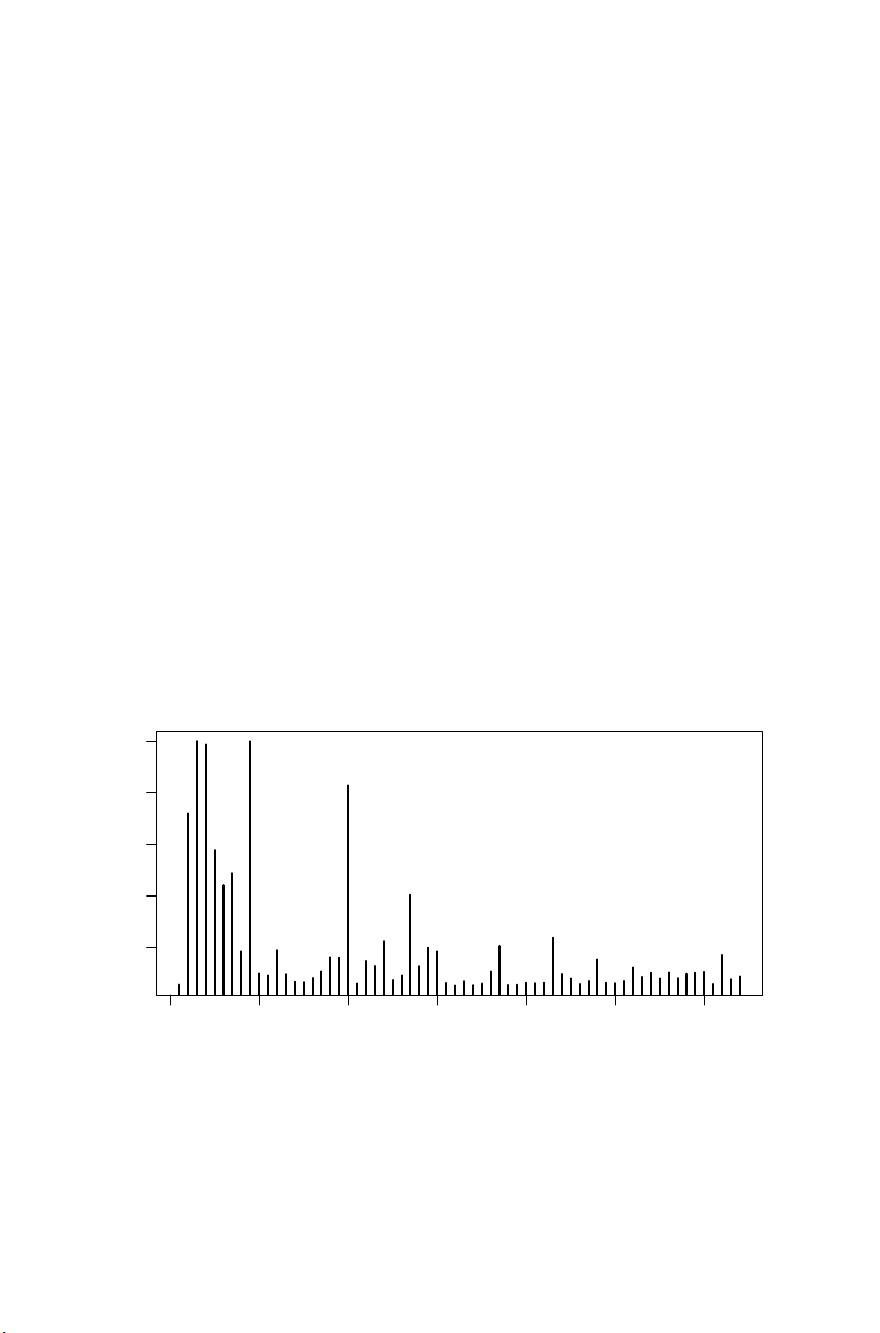
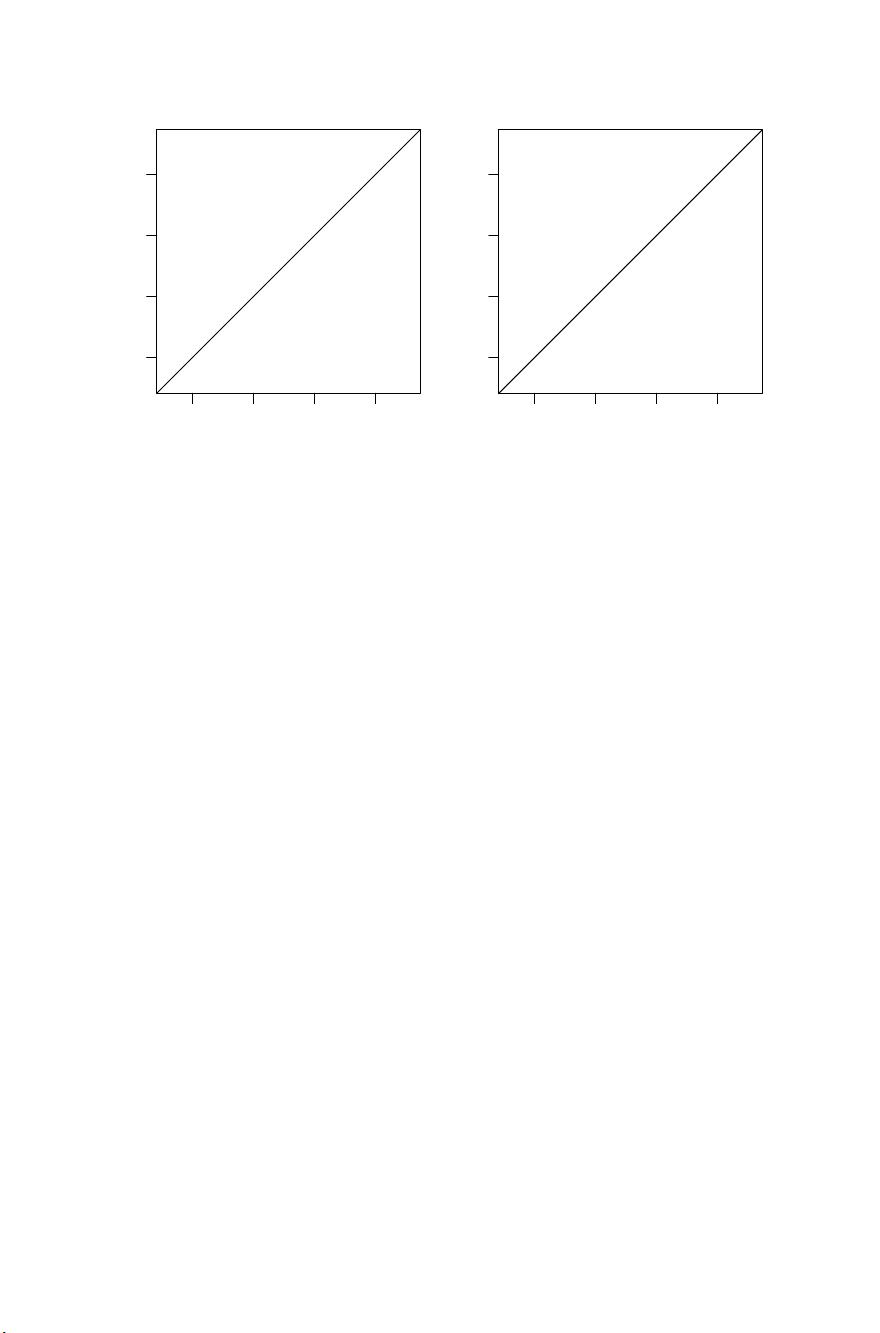
1.2.2 Building a predictive model

In Chapter 9 we will discuss an example in which our task is to build a pre-

dictive model of diabetes progression as a function of 64 baseline explanatory

variables such as age, sex and body mass index. Here we give a brief synopsis of

that example. We will ﬁrst estimate the parameters in a regression model us-

ing a “training” dataset consisting of measurements from 342 patients. We will

then evaluate the predictive performance of the estimated regression model

using a separate “test” dataset of 100 patients.

Sampling model and parameter space

Letting Y

be the diabetes progression of subject i and x

= (x

i,1

, . . . , x

i,64

)

be the explanatory variables, we will consider linear regression models of the

form

= β

i,1

+ β

i,2

+ ··· + β

i,64

+ σ

The sixty-ﬁve unknown parameters in this model are the vector of regression

coeﬃcients β = (β

, . . . , β

) as well as σ, the standard deviation of the error

term. The parameter space is 64-dimensional Euclidean s pace for β and the

positive real line for σ.

professordoctordoron@gmail.com

10 1 Introduction and examples

Predictive performance and comparison to non-Bayesian methods

We can evaluate how well this model performs by using it to predict the test

data: Let

Bayes

= E[β|y, X] be the posterior expectation of β, and let X

test

be the 100×64 matrix giving the data for the 100 patients in the test dataset.

We can compute a predicted value for each of the 100 observations in the test

set using the equation

test

= X

Bayes

. These predicted values can then be

compared to the actual observations y

test

. A plot of y

test

versus

test

appears

in the ﬁrst panel of Figure 1.4, and indicates how well

Bayes

is able to predict

diabetes progression from the baseline variables.

How does this Bayesian estimate of β compare to a non-Bayesian ap-

proach? The most commonly used estimate of a vector of regression coeﬃ-

cients is the ordinary least squares (OLS) estimate, provided in most if not all

statistical software packages. The OLS regression estimate is the value

ols

β that minimizes the sum of squares of the residuals (SSR) for the observed

data,

SSR(β) =

i=1

− β

)

and is given by the formula

ols

= (X

−1

y. Predictions for the test

data based on this estimate are given by X

ols

and are plotted against the

observed values in the second panel of Figure 1.4. Notice that using

ols

gives a weaker relationship between observed and predicted values than using

Bayes

. This can be quantiﬁed numerically by computing the average squared

prediction error,

test,i

− ˆy

test,i

)

/100, for both sets of predictions. The

prediction e rror for OLS is 0.67, about 50% higher than the value of 0.45 we

obtain using the Bayesian estimate. In this problem, even though our ad hoc

prior distribution for β only captures the basic structure of our prior beliefs

(namely, that many of the coeﬃcients are likely to be zero), this is enough to

provide a large improvement in predictive performance over the OLS estimate.

The poor performance of the OLS method is due to its inability to recog-

nize when the sample size is too small to accurately estimate the regression

coeﬃcients. In such situations, the linear relationship between the values of

y and X in the dataset, quantiﬁed by

ols

, is often an inaccurate represen-

tation of the relationship in the entire population. The standard remedy to

this problem is to ﬁt a “sparse” regression mo del, in which some or many

of the regression coeﬃcients are set to zero. One method of choosing which

coeﬃcients to set to zero is the Bayesian approach described above. Another

popular metho d is the “lasso,” introduced by Tibshirani (1996) and studied

extensively by many others. The lasso estimate is the value

lasso

of β that

minimizes SSR(β : λ), a modiﬁed version of the sum of squared residuals:

SSR(β : λ) =

i=1

− x

β)

+ λ

j=1

|β

professordoctordoron@gmail.com

1.3 Where we are going 11

●

−1 0 1 2

test

●

−1 0 1 2

test

Fig. 1.4. Observed versus predicted diabetes progression values using the Bayes

estimate (left panel) and the OLS estimate (right panel).

In other words, the lasso procedure penalizes large values of |β

|. Depending

on the size of λ, this p e nalty can make some elements of

lasso

equal to

zero. Although the lass o procedure has been motivated by and studied in

a non-Bayesian context, in fact it corresponds to a Bayesian estimate using

a particular prior distribution: The lasso estimate is equal to the posterior

mode of β in which the prior distribution for each β

is a double-exponential

distribution, a probability distribution that has a sharp peak at β

= 0.

1.3 Where we are going

As the above examples indicate, the uses of Bayesian methods are quite broad.

We have seen how the Bayesian approach provides

• models for rational, quantitative learning;

• estimators that work for small and large sample sizes;

• methods for generating statistical procedures in complicated problems.

An understanding of the beneﬁts and limits of Bayesian methods comes with

experience. In the chapters that follow, we will become familiar with these

methods by applying them to a large number of statistical models and data

analysis examples. After a review of probability in Chapter 2, we will learn

the basics of Bayesian data analysis and computation in the context of some

simple one-parameter statistical models in Chapters 3 and 4. Chapters 5, 6

and 7 discuss Bayesian inference with the normal and multivariate normal

models. While important in their own right, normal models also provide the

professordoctordoron@gmail.com

剩余269页未读，继续阅读

zhiguoxu

粉丝: 0
资源: 3

贝叶斯统计方法基础教程

贝叶斯统计方法初步教程

入门贝叶斯统计：Springer《第一堂贝叶斯统计方法课》

入门贝叶斯统计：彼得·霍夫的《贝叶斯统计基础课程》

A First Course in Bayesian Statistical Methods.pdf

A_First_Course_in_Bayesian_Statistical_Methods

Bayesian Statistical Modeling with Stan, R, and Python.pdf

Bayesian Methods for Statistical Analysis_[Puza2015]

A Bayesian Approach to Sparse Model Selection in Statistical Shape Models∗.pdf

Allegro网表转换工具Convert使用指南

若依管理存在任何文件读取漏洞检测系统，渗透测试.zip

最新资源