"格林公式及应用——曲线积分与路径无关性条件"

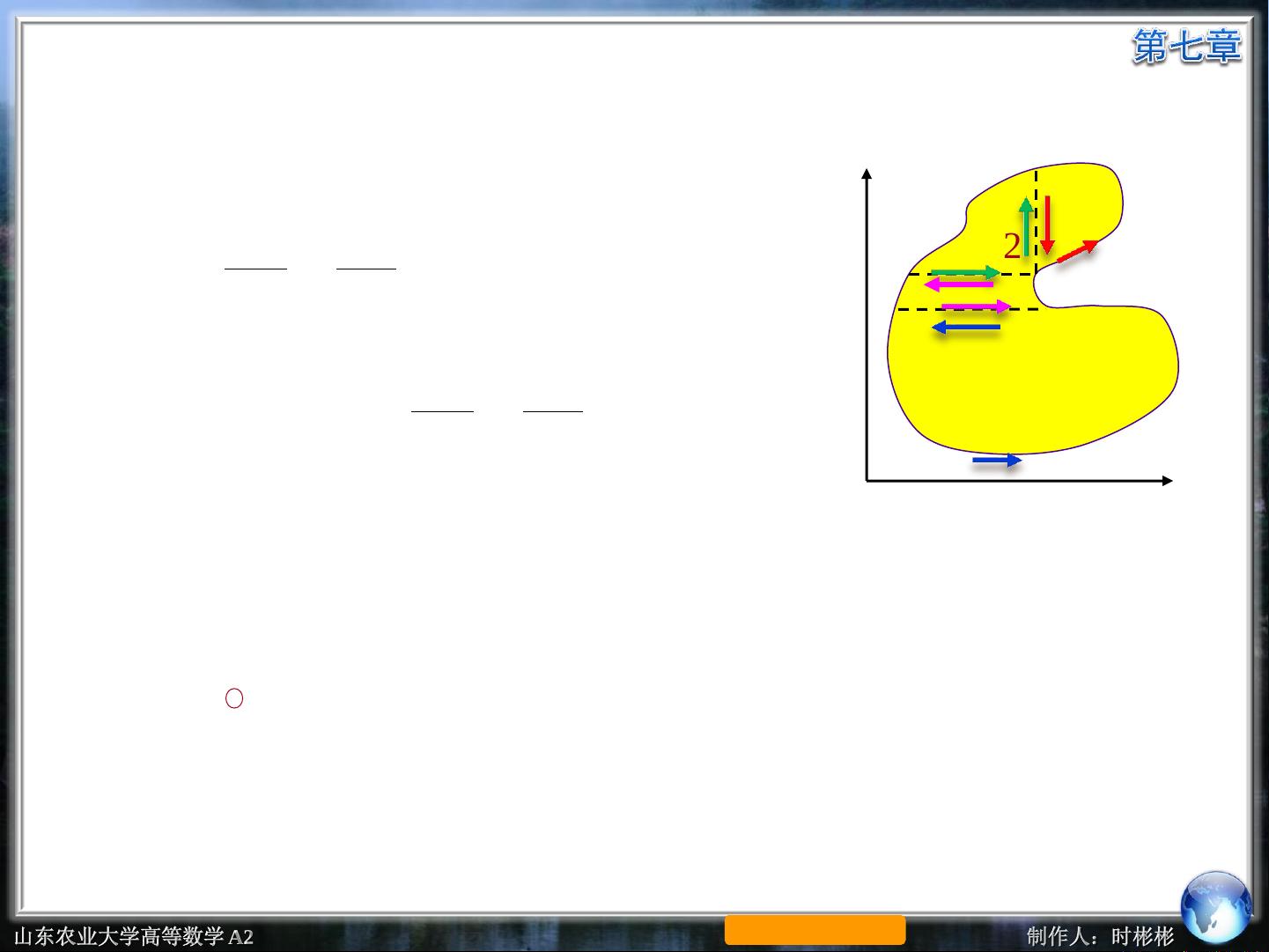
本文介绍了格林公式及其应用，着重讨论了时老师在山东农业大学高等数学 A2课程中的教学内容。格林公式是数学中的一个重要定理，它描述了曲线积分与路径无关的条件，以及全微分方程和二元函数的全微分求积。格林公式的应用涉及到曲线积分基本公式、区域D的分类和边界L的正向等概念。在具有一阶连续偏导数的函数上，格林公式可以简化曲线积分的计算，为数学分析和实际问题的求解提供了重要的工具。 本文由山东农业大学高等数学A2制作人时彬彬精心撰写，详细介绍了格林公式及其应用。在山东农业大学高等数学A2课程中，学生将通过学习格林公式来掌握曲线积分与路径无关的条件，以及全微分方程下的数学解题方法。格林公式在数学分析和工程技术中有着广泛的应用，能够简化复杂的积分运算，提高计算效率，对于学生的数学学习和实际问题的解决都具有重要意义。 格林公式是关于曲线积分的一项重要定理，它可以帮助我们理解曲线积分与路径无关的条件。在格林公式中，全微分方程du=P(x,y)dx+Q(x,y)dy的存在条件是关键，它直接影响到函数的计算方法。此外，格林公式还与区域D的分类和边界L的正向等概念密切相关，这些内容都是学生在高等数学A2课程中需要深入了解和掌握的重要知识点。 通过学习格林公式及其应用，学生不仅可以掌握基本的数学理论知识，还可以运用这些知识解决实际问题。格林公式在物理学、工程技术和计算机科学等领域都有着广泛的应用，它为实际问题的求解提供了重要的数学工具。因此，学生在学习时要认真对待这一部分内容，理解其中的数学原理和方法，以便将来能够灵活运用到实际工作中。 总之，格林公式及其应用是高等数学A2课程中的重要内容，学生需要通过深入学习和实践，掌握曲线积分与路径无关的条件，以及全微分方程和二元函数的全微分求积等知识。这些内容不仅是数学理论的基础，还与实际问题的解决密切相关，对于学生的学习和未来的发展都具有重要的意义。希望学生们能够认真对待这一部分内容，不断提高自己的数学分析能力，为将来的学习和工作打下坚实的数学基础。