"SVM(支持向量机)入门：简介、线性分类器及求解"

SVM（支持向量机）入门 SVM（Support Vector Machine）是一种常用的机器学习算法，被广泛应用于分类和回归分析中。它在20世纪90年代由Vladimir Vapnik和Alexey Chervonenkis提出，是一种传统的监督学习算法。SVM的主要思想是找到一个最优的超平面来将数据分隔开，使不同类别的样本能够尽可能地被分开。 SVM入门目录 1. SVM入门 2. SVM简介 3. 线性分类器 4. 线性分类器的求解 5. 核函数与非线性分类 6. SVM实战案例 SVM简介 SVM是一种非常强大的分类器，具有很高的准确性和泛化能力。与其他机器学习算法相比，SVM在处理高维数据和小样本数据方面更加有效。它通过将数据映射到高维空间来改善分类效果，然后在高维空间中使用超平面进行分类。 SVM能够处理两类和多类分类问题，并且对于线性和非线性分类问题都适用。对于线性可分的数据集，SVM需要找到一个能够将两类样本完全分割开的超平面。对于线性不可分的数据集，SVM通过使用核函数将数据映射到更高维度的空间，使其线性可分。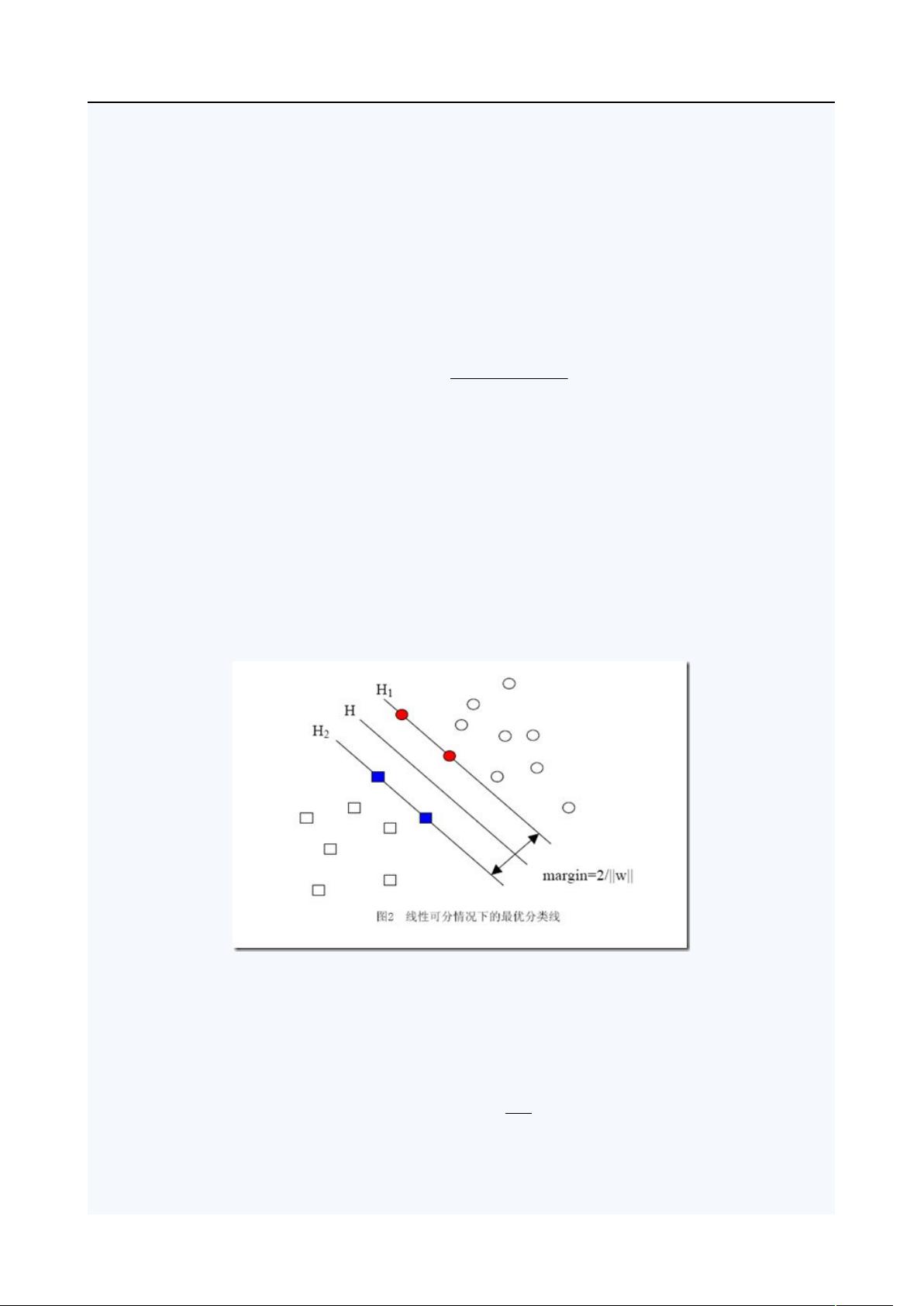 线性分类器 线性分类器是指在特征空间中使用线性函数进行分类的算法。SVM是一种常用的线性分类器，它通过在特征空间中找到一个最优的超平面来实现分类。超平面可以将数据集分为两个不同的类别，并且在超平面上离最近的样本点被称为支持向量。 线性分类器的求解 线性分类器的求解就是要找到一个最优的超平面来使得不同类别的样本能够被尽可能地分开。在SVM中，求解线性分类器可以通过最大化间隔来实现。间隔是指超平面到最近的支持向量之间的距离，最大化间隔意味着最大程度地减小分类错误。 求解线性分类器的典型方法是使用拉格朗日乘子法，并将问题转化为一个凸优化问题。通过求解凸优化问题，可以得到最优的超平面和分类边界。 核函数与非线性分类 当数据不是线性可分时，SVM使用核函数将数据映射到高维空间，以实现非线性分类。核函数可以将低维特征空间中的数据映射到高维特征空间中，使其在高维空间中线性可分。常用的核函数有线性核函数、多项式核函数和高斯核函数等。 SVM实战案例 为了更好地理解SVM的应用，可以通过实际案例进行实战演练。例如，可以使用SVM来对手写数字进行分类，或根据人的特征预测是否患有某种疾病。实战案例可以帮助我们更好地了解SVM的原理和应用。 总结 SVM是一种常用的机器学习算法，具有很高的准确性和泛化能力。它通过找到一个最优的超平面来实现分类，能够处理线性和非线性分类问题。线性分类器的求解可以通过最大化间隔来实现，而非线性分类可以通过使用核函数来实现。SVM的应用范围非常广泛，可以用于各种分类和回归问题。通过实践和研究，可以更好地理解和掌握SVM的原理和应用。