矩阵运算在统计学中的基础性作用：揭秘统计推断的数学原理

# 1. 矩阵运算在统计学中的基础性作用

矩阵运算在统计学中扮演着至关重要的角色，为统计推断和数据分析提供了坚实的基础。它允许我们表示和处理复杂的多变量数据，从而揭示数据中的模式和关系。

矩阵运算在统计学中的应用广泛，包括但不限于：

- **数据表示和变换：**矩阵可以方便地表示多维数据，并通过矩阵运算进行变换，例如中心化、标准化和降维。
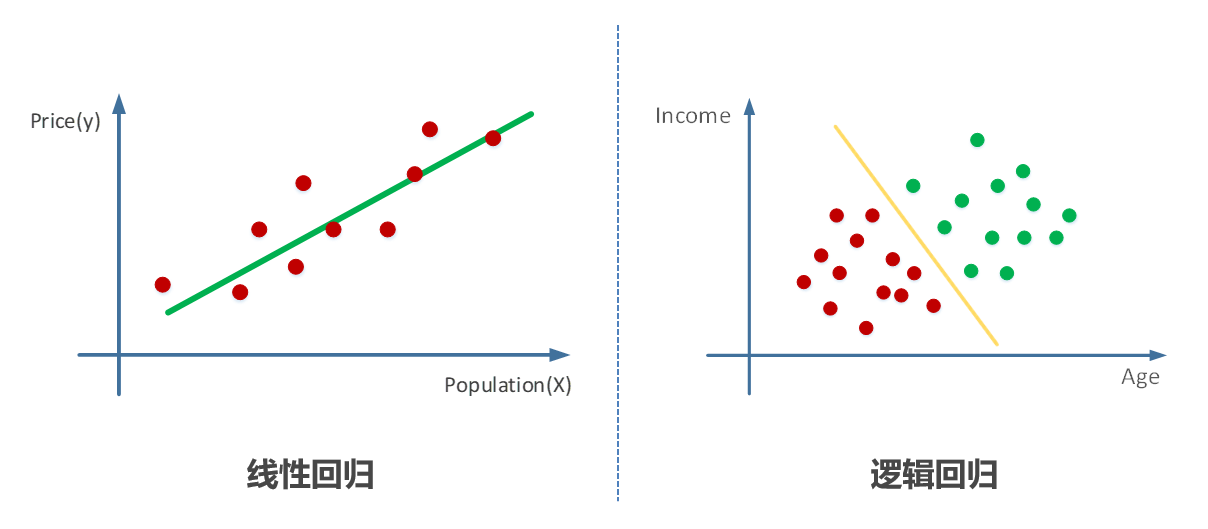
- **统计模型构建：**矩阵运算在构建统计模型中至关重要，例如线性回归和方差分析，它允许我们表示模型参数和预测值。
- **统计推断：**矩阵运算用于进行统计推断，例如参数估计和假设检验，它可以帮助我们评估模型的有效性和做出数据驱动的决策。

# 2. 矩阵运算的理论基础

矩阵运算在统计学中发挥着至关重要的作用，其理论基础根植于线性代数。线性代数为矩阵运算提供了数学框架，使其在统计推断、数据分析和机器学习中得到广泛应用。

### 2.1 线性代数基本概念

#### 2.1.1 矩阵的定义和基本运算

**矩阵定义：**矩阵是一个由数字或符号排列成的矩形数组，通常用大写字母表示，如 A、B。矩阵的元素位于行和列的交点处，用下标表示，如 a_ij 表示矩阵 A 中第 i 行第 j 列的元素。

**矩阵基本运算：**矩阵支持加法、减法和数乘等基本运算。加法和减法对相同维度的矩阵进行，对应元素相加或相减。数乘将一个标量与矩阵中的每个元素相乘。

#### 2.1.2 矩阵的行列式和逆矩阵

**行列式：**行列式是一个与矩阵关联的标量值，它反映了矩阵的行列式性质。行列式用于求解线性方程组、计算矩阵的秩和特征值。

**逆矩阵：**如果一个矩阵的行列式不为零，则它具有逆矩阵。逆矩阵是一个与原矩阵相乘得到单位矩阵的矩阵。逆矩阵用于求解线性方程组、计算矩阵的伪逆和进行矩阵变换。

### 2.2 矩阵分解与变换

矩阵分解和变换是线性代数中的重要概念，它们在统计学中有着广泛的应用。

#### 2.2.1 奇异值分解（SVD）

奇异值分解（SVD）将一个矩阵分解为三个矩阵的乘积：U、Σ 和 V^T。U 和 V^T 是正交矩阵，Σ 是一个对角矩阵，其对角线元素是矩阵 A 的奇异值。

**应用：**SVD 用于降维、数据压缩和图像处理。

#### 2.2.2 主成分分析（PCA）

主成分分析（PCA）是一种线性变换，将一组相关变量转换为一组不相关的变量，称为主成分。主成分的方差最大，可以有效地表示数据的变化。

**应用：**PCA 用于降维、数据可视化和模式识别。

**代码示例：**

import numpy as np

# 创建一个矩阵
A = np.array([[1, 2], [3, 4]])

# 求矩阵的行列式
det_A = np.linalg.det(A)
print("行列式：", det_A)

# 求矩阵的逆矩阵
inv_A = np.linalg.inv(A)
print("逆矩阵：")
print(inv_A)

# 奇异值分解
U, Sigma, Vh = np.linalg.svd(A)
print("奇异值：")
print(Sigma)

# 主成分分析
pca = PCA(n_components=1)
pca.fi