矩阵乘法的本质与优化：从理论到实战的全面解析

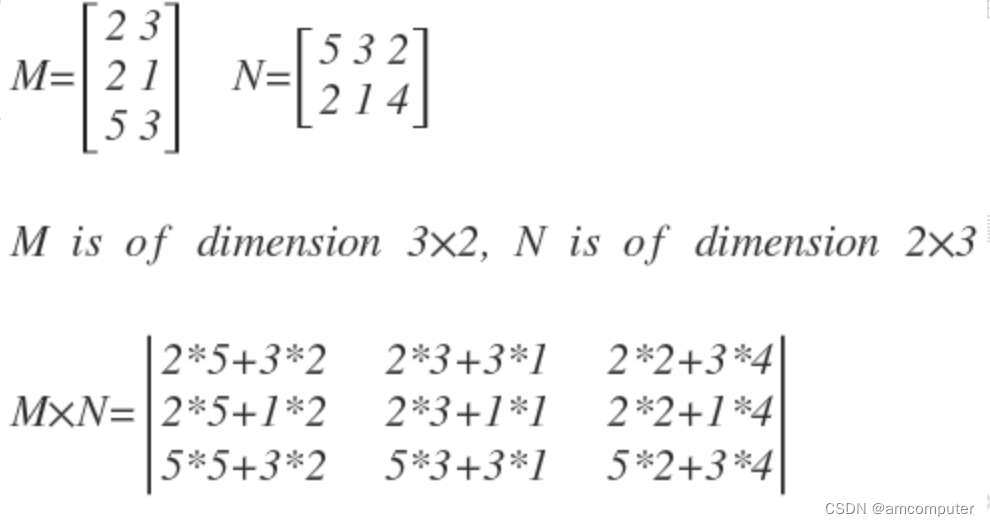
# 1. 矩阵乘法的理论基础**

矩阵乘法是线性代数中的一项基本运算，它将两个矩阵结合起来形成一个新的矩阵。矩阵乘法的定义如下：

C = A * B

其中，A和B是两个矩阵，C是它们的乘积矩阵。矩阵乘法的维度规则如下：

- A的列数必须等于B的行数。
- C的行数等于A的行数，列数等于B的列数。

# 2. 矩阵乘法的优化算法**

矩阵乘法是许多科学计算和机器学习算法的核心操作。随着数据规模的不断增长，优化矩阵乘法的性能变得至关重要。本章将探讨两种常用的矩阵乘法优化算法：分治算法和矩阵链乘优化。

## 2.1 分治算法

分治算法将矩阵乘法问题分解成较小的子问题，然后递归地解决这些子问题。这可以显著减少计算量，特别是对于大型矩阵。

### 2.1.1 Strassen算法

Strassen算法是一种分治算法，它将两个n×n矩阵的乘法分解成7个n/2×n/2矩阵的乘法。通过这种分解，Strassen算法的渐近时间复杂度从O(n^3)降低到O(n^2.81)。

def strassen(A, B):
    """Strassen算法计算两个矩阵的乘积。

    参数：
        A (numpy.ndarray): 第一个矩阵。
        B (numpy.ndarray): 第二个矩阵。

    返回：
        numpy.ndarray: 矩阵A和B的乘积。
    """
    n = A.shape[0]

    if n <= 32:
        return np.dot(A, B)

    # 将矩阵A和B分解成4个子矩阵
    A11 = A[:n//2, :n//2]
    A12 = A[:n//2, n//2:]
    A21 = A[n//2:, :n//2]
    A22 = A[n//2:, n//2:]
    B11 = B[:n//2, :n//2]
    B12 = B[:n//2, n//2:]
    B21 = B[n//2:, :n//2]
    B22 = B[n//2:, n//2:]

    # 计算7个子矩阵的乘积
    M1 = strassen(A11 + A22, B11 + B22)
    M2 = strassen(A21 + A22, B11)
    M3 = strassen(A11, B12 - B22)
    M4 = strassen(A22, B21 - B11)
    M5 = strassen(A11 + A12, B22)
    M6 = strassen(A21 - A11, B11 + B12)
    M7 = strassen(A12 - A22, B21 + B22)

    # 将子矩阵的乘积组合成最终结果
    C11 = M1 + M4 - M5 + M7
    C12 = M3 + M5
    C21 = M2 + M4
    C22 = M1 - M2 + M3 + M6

    return np.block([[C11, C12], [C21, C22]])

### 2.1.2 Coppersmith-Winograd算法

Coppersmith-Winograd算法是另一种分治算法，它将矩阵乘法问题分解成较小的子问题，然后使用快速傅里叶变换（FFT）来解决这些子问题。这可以进一步降低渐近时间复杂度，特别是对于非常大的矩阵。

## 2.2 矩阵链乘优化

矩阵链乘问题是指计算一系列矩阵乘积的最佳顺序。不同的乘积顺序会导致不同的计算量。矩阵链乘优化算法旨在找到最优的乘积顺序，以最小化计算量。

### 2.2.1 动态规划算法

动态规划算法是一种自底向上的算法，它将矩阵链乘问题分解成较小的子问题，然后逐步解决这些子问题。算法使用一个表格来存储子问题的最优解，从而避免重复计算。

def matrix_chain_order(p):
    """动态规划算法计算矩阵链乘的最佳顺序。

    参数：
        p (list): 矩阵链的维度列表。

    返回：
        tuple: 最优乘积顺序和最优计算量。
    """
    n = len(p) - 1

    # 创建表格存储子问题的最优解
    dp = [[0] * (n+1) for _ in range(n+1)]

    # 计算对角线上的最优解
    for i in range(1, n+1):
        dp[i][i] = 0

    # 逐层计算表格中的最优解
    for l in range(2, n+1):
        for i in range(1, n-l+2):
            j = i + l - 1
            dp[i][j] = float('inf')
            for k in range(i, j):
                cost = dp[i][k] + dp[k+1][j] + p[i-1] * p[k] * p[j]
                if cost < dp[i][j]:
                    dp[i][j] = cost

    # 返回最优乘积顺序和最优计算量
    return dp[1][n], dp

### 2.2.2 贪心算法

贪心算法是一种自顶向下的算法，它每次选择当前最优的子问题，然后逐步解决这些子问题。贪心算法对于矩阵链乘优化问题通常不能得到最优解，但它可以提供一个近似解。

def matrix_chain_order_greedy(p):
    """贪心算法计算矩阵链乘的近似最优顺序。

    参数：
        p (list): 矩阵链的维度列表。

    返回：
        list: 近似最优乘积顺序。
    """
    n = len(p) - 1
    order = []

    for i in range(1, n):