TensorFlow 中的模型评估与指标选择

# 1. 模型评估基础

模型评估是机器学习中至关重要的步骤，它可以帮助我们了解模型的性能并指导模型的改进。模型评估指标是衡量模型性能的定量指标，它们可以分为两大类：回归模型评估指标和分类模型评估指标。

回归模型评估指标用于评估预测值与真实值之间的差异，常见的指标包括均方误差 (MSE)、平均绝对误差 (MAE) 和根均方误差 (RMSE)。这些指标衡量预测值与真实值之间的平均误差，值越小表示模型性能越好。

分类模型评估指标用于评估模型对不同类别的预测准确性，常见的指标包括精度 (Accuracy)、召回率 (Recall) 和 F1 得分。精度衡量模型对所有样本的正确预测比例，召回率衡量模型对特定类别的正确预测比例，F1 得分是精度和召回率的加权平均。

# 2. 回归模型评估指标

回归模型用于预测连续数值，因此评估其性能需要使用量化误差度量。以下是 TensorFlow 中常用的回归模型评估指标：

### 2.1 均方误差 (MSE)

**定义和计算：**

均方误差 (MSE) 是预测值与真实值之间的平方误差的平均值。其公式为：

MSE = (1/n) * Σ(y_i - y_hat_i)^2

其中：

* n 为样本数量
* y_i 为真实值
* y_hat_i 为预测值

**优点和缺点：**

* 优点：MSE 对异常值敏感，可以有效惩罚较大的预测误差。
* 缺点：MSE 的单位与预测值的单位相同，因此在不同单位的数据集中进行比较时可能不方便。

### 2.2 平均绝对误差 (MAE)

**定义和计算：**

平均绝对误差 (MAE) 是预测值与真实值之间的绝对误差的平均值。其公式为：

MAE = (1/n) * Σ|y_i - y_hat_i|

其中：

* n 为样本数量
* y_i 为真实值
* y_hat_i 为预测值

**优点和缺点：**

* 优点：MAE 对异常值不敏感，可以更公平地评估模型在一般情况下的性能。
* 缺点：MAE 的单位与预测值的单位相同，因此在不同单位的数据集中进行比较时可能不方便。

### 2.3 根均方误差 (RMSE)

**定义和计算：**

根均方误差 (RMSE) 是 MSE 的平方根。其公式为：

RMSE = √(MSE)

**优点和缺点：**

* 优点：RMSE 的单位与预测值的单位相同，因此在不同单位的数据集中进行比较时更加方便。
* 缺点：RMSE 对异常值敏感，与 MSE 类似。

### 指标选择策略

在选择回归模型评估指标时，需要考虑以下因素：

* **数据分布：**如果数据分布是正态分布，则 MSE 和 RMSE 是合适的指标。如果数据分布偏态，则 MAE 更合适。
* **异常值：**如果数据集中存在异常值，则 MAE 更合适，因为它对异常值不敏感。
* **可解释性：**MSE 和 RMSE 的单位与预测值的单位相同，因此更容易解释。

# 3. 分类模型评估指标**

分类模型评估指标用于衡量分类模型的性能，即模型正确预测不同类别的能力。以下是一些常用的分类模型评估指标：

### 3.1 精度 (Accuracy)

**定义和计算：**

精度是分类模型最直观的评估指标，它衡量模型正确预测所有样本的比例。精度计算公式为：

accuracy = (TP + TN) / (TP + TN + FP + FN)

其中：

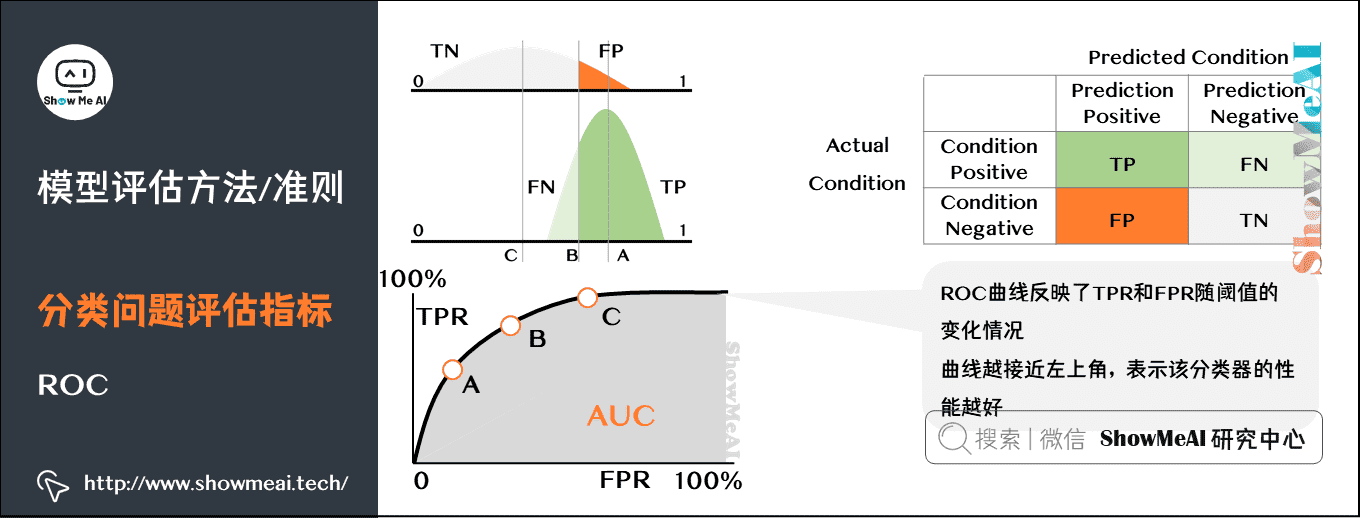
* TP：真阳性（预测为正且实际为正的样本数）
* TN：真阴性（预测为负且实际为负的样本数）
* FP：假阳性（预测为正但实际为负的样本数）
* FN：假阴性（预测为负但实际为正的样本数）

**优点和缺点：**

* **优点：**简单易懂，直观反映模型的整体预测能力。
* **缺点：**当数据集不平衡时，精度可能会失真。例如，如果数据集中有 99% 的负样本，即使模型总是预测负样本，也可以获得很高的精度。

### 3.2 召回率 (Recall)

**定义和计算：**

召回率衡量模型识别实际为正的样本的比例，计算公式为：

recall = TP / (TP + FN)

**优点和缺点：**

* **优点：**关注模型识别正样本的能力，对于不平衡数据集尤为重要。
* **缺点：**召回率高可能意味着模型预测了大量假阳性。

### 3.3 F1 得分

**定义和计算：**

F1 得分是精度和召回率的调和平均值，综合考虑了模型的整体预测能力和识别正样本的能力。计算公式为：

f1_score = 2 * (precision * recall) / (precision + recall)

其中：

precision = TP / (TP + FP)

**优点和缺点：**

* **优点：**兼顾了精度和召回率，适用于需要平衡这两个指标的情况。
* **缺点：**当精度和召回率都较低时，F1 得分也会很低。

### 3.4 评估指标的选择

选择合适的评估指标取决于具体的任务和数据集。以下是一些指导原则：

* **任务类型：**对于二分类任务，精度、召回率和 F1 得分都是常用的指标。对于多分类任务，还可以使用混淆矩阵来评估模型在不同类别上的表现。
* **数据分布：**当数据集不平衡时，精度可能会失真，此时应使用召回率或 F1 得分。
* **业务目标：**评估指标的选择也应考虑业务目标。例如，对于医疗诊断任务，召回率可能比精度更重要，因为漏诊可能导致严重后果。

### 3.5 TensorFlow 中的分类模型评估

TensorFlow 提供了丰富的评估 API，用于计算分类模型评估指标。以下是一些常用的函数：

* **tf.keras.metrics.Accuracy：**计算精度。
* **tf.keras.metrics.Recall：**计算召回率。
* **tf.keras.metrics.Precision：**计算精确率。
* **tf.keras.metrics.F1Score：**计算 F1 得分。

这些函数可以通过 `tf.keras.Model.compile` 方法添加到模型中，并在训练或评估过程中自动计算。

# 4. 指标选择策略

### 4.1 考虑任务类型

#### 4.1.1 回归任务

对于回归任务，评价模型的指标主要关注预测值与真实值之间的差异。常用的指标包括：

- **均方误差 (MSE)**：衡量预测值与真实值之间平方误差的平均值。MSE 越小，模型拟合程度越好。
- **平均绝对误差 (MAE)**：衡量预测值与真实值之间绝对误差的平均值。MAE 对异常值不敏感，因此在存在异常值时更具鲁棒性。
- **根均方误差 (RMSE)**：MSE 的平方根，表示预测值与真实值之间平方误差的平均值的平方根。RMSE 具有与 MSE 相似的含义，但单位与原始目标值相同，便于理解。

#### 4.1.2 分类任务

对于分类任务，评价模型的指标主要关注模型对不同类别的预测准确性。常用的指标包括：

- **精度 (Accuracy)**：衡量模型对所有样本预测正确的比例。精度高表示模型对不同类别的预测准确性高。
- **召回率 (Recall)**：衡量模型对特定类别样本预测正确的比例。召回率高表示模型对该类别的预测灵敏度高。
- **F1 得分**：综合考虑精度和召回率的指标，取值为 0 到 1。F1 得分越高，模型对不同类别的预测准确性和灵敏度越高。

### 4.2 考虑数据分布

#### 4.2.1 正态分布

对于正态分布的数据，MSE、MAE 和 RMSE 等指标通常是合适的。这些指标对异常值敏感，但对于正态分布的数据，异常值通常较少，因此这些指标可以提供可靠的模型评估。

#### 4.2.2 偏态分布

对于偏态分布的数据，MAE 和 RMSE 等指标可能更合适。这些指标对异常值不敏感，因此可以更准确地反映模型在偏态分布数据上的性能。

### 4.3 综合考虑

在选择指标时，需要综合考虑任务类型和数据分布。对于回归任务，通常选择 MSE、MAE 或 RMSE 等指标。对于分类任务，通常选择精度、召回率或 F1 得分等指标。对于偏态分布的数据，MAE 和 RMSE 等指标可能更合适。

# 5. TensorFlow 中的评估和指标**

**5.1 TensorFlow 中的评估 API**

TensorFlow 提供了全面的评估 API，用于计算模型的性能指标。这些 API 可分为两类：

**5.1.1 tf.keras.metrics 模块**

tf.keras.metrics 模块包含一系列内置评估指标，例如：

* tf.keras.metrics.MeanSquaredError：计算均方误差 (MSE)
* tf.keras.metrics.Accuracy：计算精度
* tf.keras.metrics.Recall：计算召回率

**5.1.2 自定义评估函数**

用户还可以创建自定义评估函数来计算特定于其任务或数据集的指标。自定义评估函数是一个 Python 函数，接受模型的预测值和真实标签作为输入，并返回一个标量值表示指标。

**5.2 TensorFlow 中的常用指标**

TensorFlow 提供了多种常用的评估指标，包括：

**5.2.1 tf.keras.metrics.MeanSquaredError**

tf.keras.metrics.MeanSquaredError 计算均方误差 (MSE)，定义为预测值与真实标签之间平方误差的平均值。MSE 用于评估回归模型，其值越小，模型的性能越好。

**5.2.2 tf.keras.metrics.Accuracy**

tf.keras.metrics.Accuracy 计算精度，定义为正确预测的样本数除以总样本数。精度用于评估分类模型，其值越高，模型的性能越好。