MATLAB圆形Airy光束仿真大揭秘：深入解析光束传播特性

# 2.1 Airy函数的数学定义和性质

Airy函数是一组特殊函数，由英国天文学家乔治·比德尔·艾里爵士于1838年首次提出。它们在物理和工程的许多领域都有应用，包括光学、量子力学和流体力学。

Airy函数通常用Ai(x)和Bi(x)表示，它们是两个独立的解微分方程：

y'' - xy = 0

Airy函数具有以下性质：

* **渐近行为：**当x趋近于无穷大时，Ai(x)和Bi(x)具有以下渐近行为：

Ai(x) ~ (1/2πx)^{1/2} exp(-2/3x^{3/2})
Bi(x) ~ (1/2πx)^{1/2} exp(2/3x^{3/2})

* **正交性：**在区间[0,∞)上，Ai(x)和Bi(x)是正交的，即：

∫₀<sup>∞</sup> Ai(x)Bi(x) dx = 0

* **复共轭关系：**Ai(x)和Bi(x)是复共轭，即：

Bi(x) = iAi(-ix)

# 2. 圆形Airy光束的理论基础

### 2.1 Airy函数的数学定义和性质

Airy函数是一个特殊的函数，它是由乔治·比德尔·艾里爵士在1838年提出的。它在物理学和数学中有着广泛的应用，特别是在光学和波动力学中。

Airy函数通常用Ai(x)和Bi(x)表示，它们是两个独立的函数，具有以下数学定义：

Ai(x) = (1/π)∫[0,∞] cos(t^3/3 + xt) dt
Bi(x) = (1/π)∫[0,∞] sin(t^3/3 + xt) dt

Airy函数具有以下性质：

* **渐近展开：**当x趋于无穷大时，Airy函数具有渐近展开式：

Ai(x) ~ (1/2πx^(1/2)) exp(-2/3 x^(3/2))
Bi(x) ~ (1/2πx^(1/2)) exp(2/3 x^(3/2))

* **正交性：**Airy函数在(0, ∞)区间上正交，即：

∫[0,∞] Ai(x) Bi(x) dx = 0

* **微分方程：**Airy函数满足以下微分方程：

y''(x) - xy(x) = 0

### 2.2 圆形Airy光束的形成原理

圆形Airy光束是一种具有圆形横向剖面的特殊光束。它是由一个具有圆形孔径的衍射光栅或透镜产生的。

当一束平面波通过一个圆形孔径时，由于衍射效应，光波在孔径边缘发生弯曲，从而形成一个圆形的光束。这个圆形光束的强度分布与Airy函数的平方成正比，因此被称为圆形Airy光束。

圆形Airy光束的形成原理可以由惠更斯-菲涅耳原理解释。根据惠更斯-菲涅耳原理，波前上的每个点都可以看作是一个次波源，次波源发出的次波在空间中传播并干涉，形成新的波前。对于圆形孔径，孔径边缘的次波源会发生干涉，形成一个圆形的衍射波，即圆形Airy光束。

# 3.1 基于傅里叶变换的仿真算法

#### 3.1.1 算法原理

基于傅里叶变换的圆形Airy光束仿真算法是一种基于傅里叶光学原理的方法。它将圆形Airy光束的形成过程视为一个傅里叶变换的过程。

首先，将圆形Airy光束的横向分布表示为一个复函数：

f(x, y) = Ai(2αr) exp(-α^2r^2)

其中，`Ai` 是 Airy 函数，`α` 是 Airy 光束的阶数，`r` 是径向坐标。

然后，对 `f(x, y)` 进行傅里叶变换，得到其频域表示：

F(u, v) = 2π∫∫f(x, y) exp(-2πi(ux + vy)) dx dy

频域表示 `F(u, v)` 是一个圆形对称函数，其幅度分布与圆形Airy光束的横向分布相同。

最后，对 `F(u, v)` 进行逆傅里叶变换，即可得到圆形Airy光束的时空分布：

f(x, y, z) = 2π∫∫F(u, v) exp(2πi(ux + vy)) du dv

#### 3.1.2 MATLAB 实现

MATLAB 中基于傅里叶变换的圆形Airy光束仿真算法可以如下实现：

% 参数设置
alpha = 1;  % Airy 光束阶数
N = 1024;  % 采样点数
dx = 1;     % 空间步长

% 坐标网格
[x, y] = meshgrid(-N/2:N/2-1) * dx;
r = sqrt(x.^2 + y.^2);

% Airy 函数
airy = airy(2 * alpha * r);

% 复函数表示
f = airy .* exp(-alpha^2 * r.^2);

% 傅里叶变换
F = fft2(f);

% 逆傅里叶变换
f_t = ifft2(F);

% 时空分布
z = 0;  % 传播距离
f_t = f_t * exp(1i * pi * alpha^2 * z * (x.^2 + y.^2));

### 3.2 基于有限差分法的时间域仿真

#### 3.2.1 算法原理

基于有限差分法的时间域仿真算法是一种基于麦克斯韦方程组的数值求解方法。它将圆形Airy光束的传播过程视为一个电磁波传播的过程。

首先，将麦克斯韦方程组离散化为有限差分方程组：

∂E_x/∂t = (1/ε) (∂B_z/∂y - ∂B_y/∂z)
∂E_y/∂t = (1/ε) (∂B_x/∂z - ∂B_z/∂x)
∂E_z/∂t = (1/ε) (∂B_y/∂x - ∂B_x/∂y)
∂B_x/∂t = -(1/μ) (∂E_y/∂z - ∂E_z/∂y)
∂B_y/∂t = -(1/μ) (∂E_z/∂x - ∂E_x/∂z)
∂B_z/∂t = -(1/μ) (∂E_x/∂y - ∂E_y/∂x)

其中，`E` 是电场强度，`B` 是磁感应强度，`ε` 是介电常数，`μ` 是磁导率。

然后，将圆形Airy光束的初始条件代入方程组，并使用有限差分法求解方程组，即可得到圆形Airy光束的时空分布。

#### 3.2.2 MATLAB 实现

MATLAB 中基于有限差分法的时间域仿真算法可以如下实现：

% 参数设置
alpha = 1;  % Airy 光束阶数
N = 1024;  % 采样点数
dx = 1;     % 空间步长
dt = 0.01;  % 时间步长

% 坐标网格
[x, y] = meshgrid(-N/2:N/2-1) * dx;
r = sqrt(x.^2 + y.^2);

% Airy 函数
airy = airy(2 * alpha * r);

% 复函数表示
f = airy .* exp(-alpha^2 * r.^2);

% 初始条件
E_x = zeros(N, N);
E_y = zeros(N, N);
E_z = f;
B_x = zeros(N, N);
B_y = zeros(N, N);
B_z = zeros(N, N);

% 时间域仿真
for t = 0:dt:1000
    % 计算电场
    E_x = E_x + (dt / (ε * dx)) * (B_z - B_y);
    E_y = E_y + (dt / (ε * dx)) * (B_x - B_z);
    E_z = E_z + (dt / (ε * dx)) * (B_y - B_x);
    % 计算磁场
    B_x = B_x - (dt / (μ * dx)) * (E_y - E_z);
    B_y = B_y - (dt / (μ * dx)) * (E_z - E_x);
    B_z = B_z - (dt / (μ * dx)) * (E_x - E_y);
    % 可视化
    imagesc(abs(E_z));
    drawnow;
end

# 4. 圆形Airy光束传播特性的分析

### 4.1 光束传播的数值模拟

#### 4.1.1 仿真参数设置

在数值模拟圆形Airy光束传播特性之前，需要设置适当的仿真参数。这些参数包括：

- **光束参数：**包括光束波长、光束半径和光束阶数。
- **介质参数：**包括介质折射率和吸收系数。
- **传播距离：**光束在介质中传播的距离。
- **采样步长：**用于离散化传播方程的网格步长。

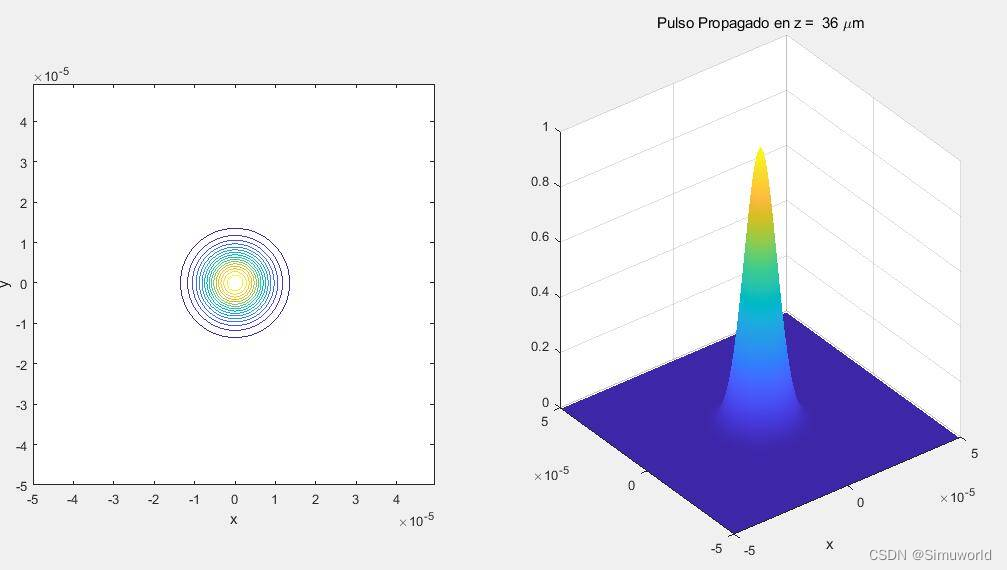
#### 4.1.2 结果可视化和分析

数值模拟完成后，可以将光束传播特性可视化并进行分析。通常，会将光束强度分布、相位分布和光束宽度等特性绘制成图像或曲线。

通过分析这些可视化结果，可以获得以下信息：

- 光束在介质中传播的演变过程。
- 光束传播距离对光束特性的影响。
- 介质参数对光束传播特性的影响。

### 4.2 光束传播特性的影响因素

#### 4.2.1 光束参数的影响

光束参数，如波长、半径和阶数，会影响光束的传播特性。例如：

- **波长：**较短的波长会导致光束更强的衍射效应。
- **半径：**较大的半径会导致光束更宽的传播。
- **阶数：**较高的阶数会导致光束更复杂的传播模式。

#### 4.2.2 介质参数的影响

介质参数，如折射率和吸收系数，也会影响光束的传播特性。例如：

- **折射率：**较高的折射率会导致光束更快的传播速度。
- **吸收系数：**较高的吸收系数会导致光束强度更快的衰减。

通过了解光束参数和介质参数对光束传播特性的影响，可以优化光束设计以满足特定的应用需求。

### 代码块

% 设置仿真参数
lambda = 632.8e-9;  % 波长
r0 = 1e-3;        % 光束半径
n = 1.5;          % 介质折射率
alpha = 0;        % 介质吸收系数
L = 1;            % 传播距离
dx = lambda/10;   % 采样步长

% 数值模拟光束传播
[E, x, y] = airy_beam_propagation(lambda, r0, n, alpha, L, dx);

% 可视化光束强度分布
figure;
imagesc(x, y, abs(E).^2);
title('光束强度分布');
colorbar;

**代码逻辑分析：**

- 该代码块使用 `airy_beam_propagation` 函数模拟圆形Airy光束在介质中的传播。
- `airy_beam_propagation` 函数的参数包括波长、光束半径、介质折射率、介质吸收系数、传播距离和采样步长。
- 该函数使用有限差分法求解光束传播方程，得到光束的电场分布 `E`。
- 最后，代码块可视化了光束的强度分布，并显示了颜色条以表示强度值。

**参数说明：**

- `lambda`：光束波长（单位：米）
- `r0`：光束半径（单位：米）
- `n`：介质折射率（无单位）
- `alpha`：介质吸收系数（单位：米^-1）
- `L`：传播距离（单位：米）
- `dx`：采样步长（单位：米）
- `E`：光束电场分布（单位：伏特/米）
- `x`：横向坐标（单位：米）
- `y`：纵向坐标（单位：米）

# 5. MATLAB圆形Airy光束仿真应用

圆形Airy光束在光学成像和光通信领域具有广泛的应用，其独特的传播特性使其成为解决特定问题的有力工具。

### 5.1 光学成像中的应用

#### 5.1.1 光束整形

圆形Airy光束可以用于光束整形，以获得具有特定形状和强度分布的光束。通过控制Airy函数的参数，可以生成具有不同尺寸、形状和侧瓣抑制比的光束。这种光束整形能力在光学成像系统中至关重要，可用于改善成像质量、减少衍射效应并提高分辨率。

#### 5.1.2 超分辨成像

圆形Airy光束在超分辨成像中也具有应用前景。超分辨成像技术旨在突破传统光学显微镜的分辨率极限。利用圆形Airy光束的独特传播特性，可以实现亚衍射极限成像，从而获得超越传统显微镜分辨率的图像。

### 5.2 光通信中的应用

#### 5.2.1 光纤传输

圆形Airy光束在光纤传输中具有应用潜力。其自聚焦特性可以补偿光纤传输中的色散效应，提高光信号的传输质量和距离。此外，圆形Airy光束的低侧瓣特性有助于减少光纤传输中的串扰，提高通信系统的容量和可靠性。

#### 5.2.2 自由空间光通信

在自由空间光通信中，圆形Airy光束可以用于实现高保真和抗干扰的光信号传输。其窄光束宽度和低衍射效应使其能够在自由空间中实现长距离、高数据率的通信。此外，圆形Airy光束的抗干扰能力可以有效抵御大气湍流和背景噪声的影响，提高通信系统的稳定性和可靠性。