全排序策略全解析：MapReduce Shuffle中的完整排序流程

# 1. 全排序策略概述

## 1.1 排序策略的重要性
在分布式计算框架中，排序是一个不可或缺的环节，尤其是在MapReduce模型下，排序策略的合理选择直接关系到数据处理的效率和准确性。全排序策略正是在保证数据全局有序的基础上，对数据处理流程进行优化的一种方法。

## 1.2 全排序与其他排序的区别
全排序策略与其他排序方法的主要区别在于它关注于使所有数据集中有序，而局部排序或部分排序可能只关注数据片段的有序性。全排序能够简化后续的数据处理流程，例如在需要数据全局有序的业务场景中表现出色。

## 1.3 全排序策略的适用场景
全排序策略最适合的应用场景包括数据分析、报表生成以及需要全局排序结果的业务逻辑处理。然而，它可能会带来较高的资源消耗，特别是在处理大规模数据集时。因此，在实际应用中，需要根据具体需求和资源条件权衡选择使用全排序策略。

# 2. MapReduce Shuffle机制基础

## 2.1 Shuffle的定义和作用

### 2.1.1 MapReduce框架的简要回顾

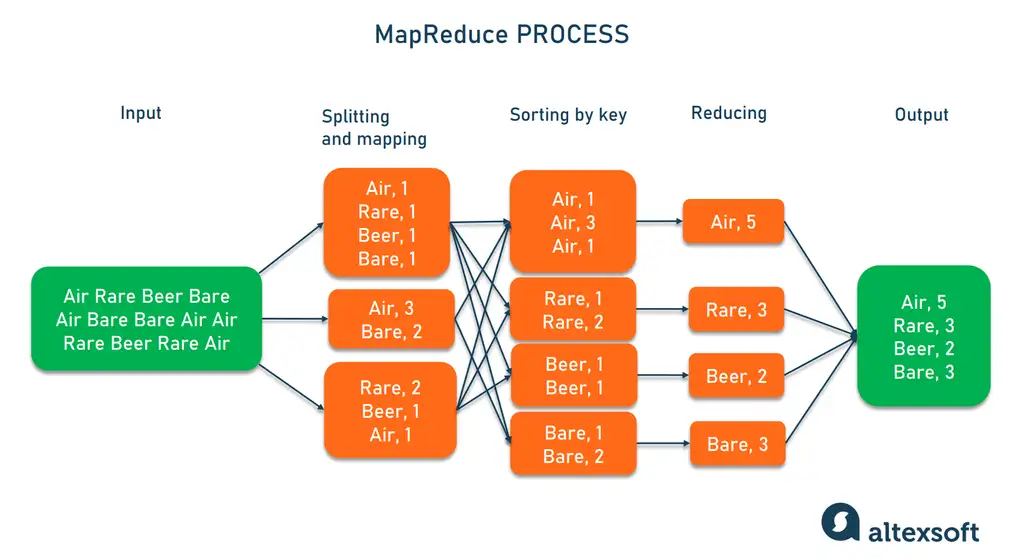
在深入探讨Shuffle机制之前，我们有必要先回顾一下MapReduce框架的基本运作原理。MapReduce是一种编程模型，用于处理大规模数据集的并行运算。这个模型由两部分组成：Map阶段和Reduce阶段。Map阶段处理输入数据，生成一系列中间键值对（key-value pairs），而Reduce阶段则将具有相同键（key）的所有值（values）合并起来。

MapReduce框架隐藏了底层的数据分布式存储和计算细节，使开发者能够专注于业务逻辑的实现。在Hadoop这样的分布式计算平台中，MapReduce通过多个节点并行处理数据，从而实现高效的计算能力。

### 2.1.2 Shuffle在数据处理中的重要性

Shuffle是MapReduce中非常关键的一个环节，它负责在Map和Reduce阶段之间传输数据，确保每个Reduce任务能够接收到所有Map任务输出中对应其键（key）的数据。Shuffle的性能直接影响到整个MapReduce作业的执行速度和效率。

在Shuffle过程中，数据需要跨网络传输，并在Reduce节点上进行排序和合并。此过程中可能会涉及大量的磁盘I/O操作和内存管理。一个优化得当的Shuffle机制可以最大限度地减少不必要的数据传输，减少磁盘I/O瓶颈，提升MapReduce作业的性能。

## 2.2 Shuffle的关键组件和流程

### 2.2.1 Map端的Shuffle流程

Map端Shuffle主要涉及到数据的输出和写入到磁盘，以及网络传输的初步准备。首先，Map任务在处理完输入数据后，会生成键值对。这些键值对需要按照键进行分区，并在内存中进行排序，然后写入到磁盘上。

在Map端，数据的分区和排序是Shuffle过程中的重要步骤。通过分区，确保相同键的数据被分配到同一个Reducer，而排序则是为了优化网络传输和Reduce端的处理效率。Map端输出的数据会通过一个"Spill"过程，当内存中的数据达到一定的阈值时，就会被写入到磁盘上，同时还在内存中保留一部分空间以继续处理后续的数据。

### 2.2.2 Reduce端的Shuffle流程

Reduce端Shuffle的开始于从Map端获取数据。这一阶段包括三个主要步骤：数据拷贝、合并排序以及最终的输出。

在数据拷贝阶段，Reduce任务会向所有的Map任务发起请求，以获取其需要处理的键值对数据。这些数据可能是从不同的Map任务中得到的，因此需要进行合并排序。合并排序是一个多路归并的过程，它在内存中对数据进行排序，并处理掉重复的键值对。这个过程需要仔细地管理内存使用，以避免溢出。

完成合并排序后，排序好的数据会被送入到Reduce函数进行处理，最终生成输出结果。这个结果可以是存储在HDFS上，也可以是输出到其他存储系统或应用接口中。

在接下来的章节中，我们将更深入地探讨这些组件的细节，并给出实际操作中的优化建议和实现方法。

# 3. 全排序策略的理论基础

## 3.1 排序算法的分类和特点

排序算法是计算机科学中一个重要的领域，它广泛应用于各种数据处理场景。根据数据存储的不同，排序算法主要分为内部排序和外部排序两大类。

### 3.1.1 内部排序与外部排序

**内部排序**主要针对内存中的数据进行排序，如快速排序、堆排序等。这些排序算法通常具有较好的时间复杂度，能够快速地对较小规模的数据集合进行排序。内部排序的执行速度受到数据规模的直接影响，对于大数据集，它们的效率会显著下降。

# 快速排序的一个简单实现
def quicksort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quicksort(left) + middle + quicksort(right)

array = [3, 6, 8, 10, 1, 2, 1]
print(quicksort(array))

快速排序的平均时间复杂度为O(n log n)，其主要步骤包括选择基准(pivot)、分区(partition)和递归排序子数组。它采用分治策略，将问题分解成较小的问题来解决。

**外部排序**则用于处理超出内存容量的大文件或数据流，如外部归并排序。在大数据处理中，外部排序扮演着关键角色，它通过将数据分块，逐步处理和合并，最终完成整个数据集的排序。外部排序的核心在于如何高效地使用磁盘I/O。

### 3.1.2 常见排序算法的比较

除了快速排序和归并排序，常见的排序算法还包括插入排序、冒泡排序、选择排序等。这些算法在不同场景下的效率各有千秋，选择合适的排序算法取决于数据的大小、数据的初始顺序、是否稳定排序等因素。

以下是常见的排序算法对比表：

| 排序算法 | 最佳时间复杂度 | 平均时间复杂度 | 最差时间复杂度 | 空间复杂度 | 稳定性 |
|----------|----------------|----------------|----------------|------------|--------|
| 快速排序 | O(n log n) | O(n log n) | O(n^2) | O(log n) | 不稳定 |
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) | 稳定 |
| 插入排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 冒泡排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 |

对于全排序策略而言，稳定性和效率是重要的考量因素，因为它需要保证数据在排序后的顺序与原始输入顺序一致，同时要求在大