【自定义散列函数实战】：为不同数据类型设计最佳散列方案

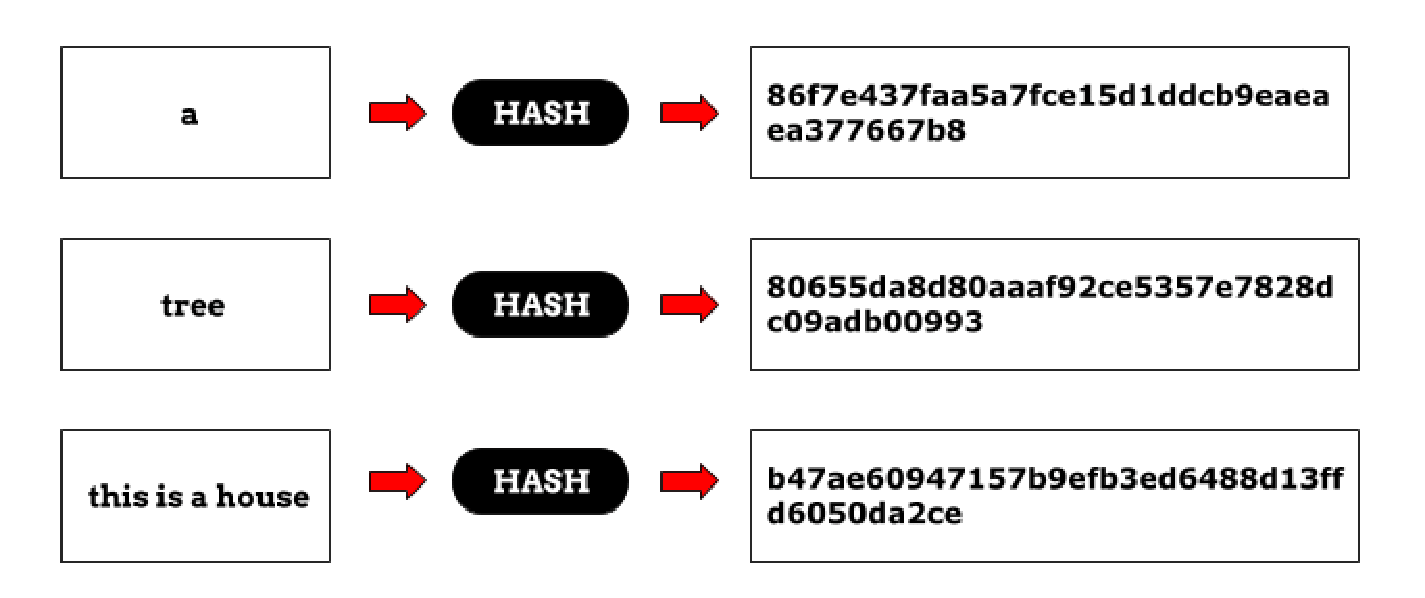
# 1. 散列函数的基本概念与应用

在计算机科学中，散列函数是将输入（也称为“键”）转换成固定长度输出的过程，输出通常被称为散列值或散列码。散列函数在数据存储和检索方面有着广泛的应用，包括数据库索引、缓存机制、密码存储等。它的设计要求在不同的输入中产生均匀分布的输出，以最小化潜在的冲突并实现快速查找。

散列函数的应用非常多样，可以在数据结构中用作快速数据检索的基础。例如，在哈希表中，散列函数被用来计算键的索引，从而实现对数据项的快速访问。此外，在密码学中，散列函数是安全通信不可或缺的一部分，用于确保数据的完整性和验证。

本章将详细探讨散列函数的基本概念、特性以及它们的实际应用，为后续章节中更深入的理论基础和优化策略奠定基础。通过本章的学习，读者将对散列函数有初步的了解，并掌握其在不同场景下的应用方法。

# 2. 散列函数的理论基础

## 2.1 散列函数的定义和特性

### 2.1.1 散列函数的定义及其重要性

散列函数，又称哈希函数，是将任意长度的输入（通常称为"键"或"消息"）通过散列算法处理，映射成固定长度输出的函数。输出通常是一个哈希值或哈希码，它通常用来检查数据的完整性，实现快速查找和存储。散列函数的重要性在于它能够在数学上保证输入数据与输出哈希值之间的唯一对应性，使得散列成为一种强大的数据结构和算法工具。

散列函数在计算机科学中应用广泛，从数据存储、安全加密到数据检索，几乎在所有需要高效处理数据的场合都有应用。例如，散列表（哈希表）就是基于散列函数的原理，用来存储键值对，以便于快速访问。

### 2.1.2 散列函数的基本性质和要求

散列函数应该满足以下基本性质，以保证其在实际应用中的有效性：

- **确定性**：对同一输入，散列函数必须产生相同的输出。
- **高效性**：计算散列值应能在合理的时间内完成。
- **均匀分布**：不同的输入值应当尽可能均匀地分布在整个哈希空间中。
- **避免碰撞**：尽量减少不同输入值产生相同哈希值的概率。

在实现时，虽然完全避免碰撞是不可能的，但设计良好的散列函数能够最大限度地减少碰撞发生的可能性。

## 2.2 散列函数的设计原则

### 2.2.1 冲突解决策略

冲突解决是散列函数设计中的重要环节。冲突指的是不同的键值在散列函数作用下产生相同的哈希值。常见的冲突解决策略有：

- **开放寻址法**：当发生冲突时，按照某种规则在散列表中寻找下一个空槽位。
- **链地址法**：把所有哈希到同一个槽位的元素构成一个链表，发生冲突时将元素加入到链表中。
- **再散列技术**：为发生冲突的键计算新的哈希值，直到找到一个空槽位。

### 2.2.2 均匀分布原则

散列函数需要尽可能保证输出的哈希值均匀分布在整个哈希空间内。均匀分布原则有利于减少冲突的概率，提高数据检索的效率。常见的措施包括：

- 使用高质量的随机数生成器。
- 确保哈希函数的输出值域足够大。
- 对于键的每一位，都应尽可能影响最终的哈希值。

### 2.2.3 动态扩容机制

随着数据量的增加，原本设计良好的哈希表可能会因为装载因子过高而需要扩容。动态扩容机制能够保证在不断增长的数据量下，哈希表的性能依然稳定。实现这一机制的关键步骤包括：

- 监测当前哈希表的装载因子。
- 当装载因子超过预设阈值时，创建一个新的更大的哈希表。
- 将旧哈希表中的数据重新散列并迁移到新的哈希表中。

## 2.3 散列函数的性能评估

### 2.3.1 时间复杂度和空间复杂度

对于散列函数而言，性能评估主要涉及两个重要指标：时间复杂度和空间复杂度。对于大多数散列函数：

- 时间复杂度通常为O(1)，即查找、插入和删除操作的时间不依赖于数据集的大小。
- 空间复杂度则与散列表的大小直接相关，理想情况下散列函数会尽量利用空间，减少不必要的浪费。

### 2.3.2 冲突率和装载因子

冲突率和装载因子是衡量散列函数性能的重要指标：

- **装载因子**是已占用槽位数与散列表总槽位数的比率。装载因子越大，发生冲突的概率越高。
- **冲突率**指的是在散列表中发生冲突的键值对所占的比例。好的散列函数设计应尽量降低冲突率。

### 2.3.3 安全性和抗碰撞性评估

在密码学和安全验证等场合，散列函数还需要具备安全性和抗碰撞性。具体而言：

- **安全性**意味着从散列值反向推导原始数据是不可行的，或者这种尝试成本高昂。
- **抗碰撞性**是指找到两个不同输入值，它们具有相同哈希值的难度，这对于密码学至关重要。

例如，MD5 和 SHA-1 等加密散列算法在安全性方面存在已知漏洞，因此在实际应用中更倾向于使用 SHA-2 和 SHA-3 等更为安全的算法。

# 3. 不同数据类型的散列方案设计

## 3.1 整型数据的散列函数设计

### 3.1.1 整型数据的特点和要求

整型数据作为计算机中最基础的数据类型之一，在散列函数设计中也有着广泛的应用。整型数据的散列函数设计需要考虑到整型数据的特点：固定长度，数值范围明确。由于整型数据的长度和取值范围确定，其散列函数的设计相对简单。设计上，需要确保对整型数据的每一个可能值，都能映射到哈希表中唯一的槽位上，尽量减少冲突。

整型散列函数的设计原则如下：

- 保证散列值的分布均匀，避免数据聚集。
- 尽量减少计算复杂度，保证散列函数的效率。
- 考虑到哈希表的扩容，设计时应便于动态调整。

### 3.1.2 典型算法：DJB2和FNV

DJB2和FNV是两种经典的针对整型数据设计的散列函数。DJB2是Daniel J. Bernstein设计的一个高效散列函数，而FNV（Fowler–Noll–Vo）是另一款广泛使用的散列算法。

#### DJB2算法

unsigned long djb2(unsigned char *str) {
    unsigned long hash = 5381;
    int c;

    while ((c = *str++))
        hash = ((hash << 5) + hash) + c; /* hash * 33 + c */

    return hash;
}

DJB2算法通过不断地左移和累加，对输入的字符串（这里以字符数组为例）进行散列计算。每次循环将当前字符的ASCII值与33相乘，再与当前的散列值左移五位后的值相加，最终得到散列值。

#### FNV算法

unsigned long fnv(unsigned char *str, size_t len) {
    unsigned long hash = 0x811c9dc5; // 初始值
    size_t i;

    for (i = 0; i < len; i++) {
        hash = hash ^ str[i];
        hash = hash * 0x***; // 乘以素数
    }

    return hash;
}

FNV算法同样是一个逐字节计算散列值的算法，其算法的特点是使用了一个固定的大素数0x***来进行乘法操作。这个素数对于避免生成的散列值聚集在哈希表的某些区域特别有效。

### 3.2 字符串数据的散列函数设计

#### 3.2.1 字符串数据的处理难点