特征向量流形学习：揭示数据中的非线性关系，探索隐藏结构

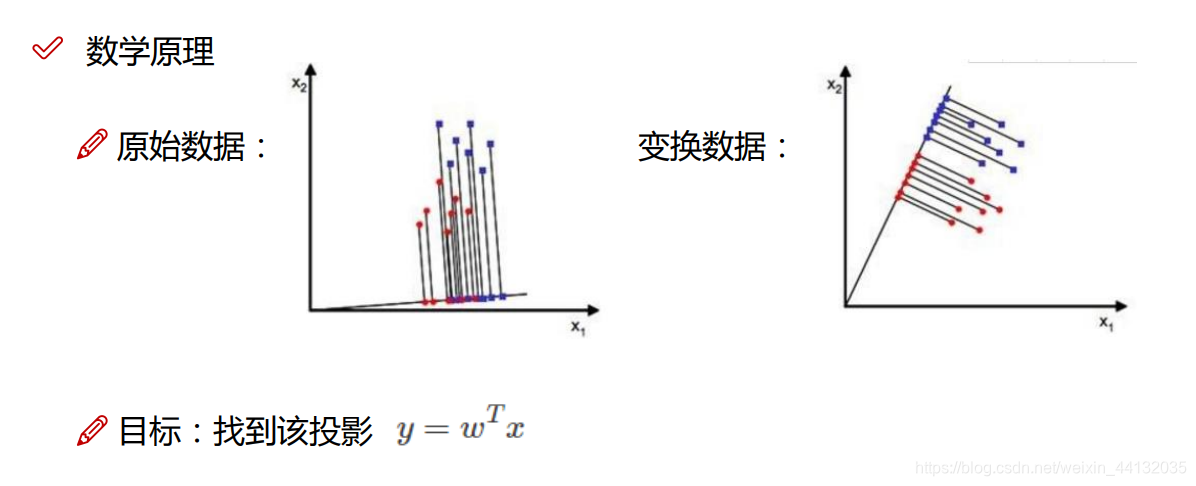
# 1. 特征向量流形学习概述

流形学习是一种非线性降维技术，旨在将高维数据映射到低维流形上，保留数据的内在结构和几何关系。与线性降维方法（如主成分分析）不同，流形学习假设数据分布在非线性流形上，而不是线性子空间中。

流形学习算法通过局部邻域关系构建数据点的相似性图，并利用这些关系来构造低维嵌入。这些算法旨在保留数据的局部结构，同时忽略噪声和异常值。通过将数据映射到低维流形上，流形学习可以实现降维、可视化和非线性关系建模。

# 2. 流形学习理论

### 2.1 流形概念与特征空间

**流形概念**

流形是一种几何对象，它在局部表现为一个低维子空间，但在全局却可能嵌入到高维空间中。流形可以用来描述复杂数据在高维空间中的内在结构。

**特征空间**

特征空间是将原始数据映射到一个新的空间，其中数据的内在结构更加明显。流形学习算法的目标是找到一个低维特征空间，使得数据在该空间中表现为一个流形。

### 2.2 流形学习算法原理

流形学习算法通过局部邻域关系来构建数据之间的低维流形结构。常见的流形学习算法包括：

#### 2.2.1 局部线性嵌入（LLE）

**原理**

LLE假设数据在局部邻域内表现为线性关系。它通过最小化局部邻域内数据的重构误差来构造低维流形。

**步骤**

1. 对于每个数据点，找到其 k 个最近邻。
2. 构建局部邻域内的权重矩阵 W，其中 W(i, j) 表示数据点 i 和 j 之间的权重。
3. 求解最小化重构误差的目标函数：

min ||X - WLX||^2

其中 X 是原始数据，L 是拉普拉斯矩阵，由 W 计算得到。

**代码块**

import numpy as np
from sklearn.neighbors import NearestNeighbors

def lle(X, k=5):
    """
    局部线性嵌入算法

    参数：
        X: 原始数据，形状为 (n_samples, n_features)
        k: 最近邻数

    返回：
        Y: 降维后的数据，形状为 (n_samples, n_components)
    """

    # 构建最近邻图
    neigh = NearestNeighbors(n_neighbors=k)
    neigh.fit(X)
    neighbors = neigh.kneighbors(X, return_distance=False)

    # 构建权重矩阵
    W = np.zeros((X.shape[0], X.shape[0]))
    for i in range(X.shape[0]):
        for j in neighbors[i]:
            W[i, j] = 1 / np.linalg.norm(X[i] - X[j])

    # 求解拉普拉斯矩阵
    L = np.diag(np.sum(W, axis=1)) - W

    # 求解特征值和特征向量
    eigvals, eigvecs = np.linalg.eig(L)

    # 降维
    Y = eigvecs[:, 1:k+1]

    return Y

**逻辑分析**

LLE 算法通过构建局部邻域内的权重矩阵 W，然后求解拉普拉斯矩阵 L 的特征值和特征向量来降维。特征值越小，对应的特征向量越能表示数据在流形上的局部线性结构。

#### 2.2.2 主成分分析（PCA）

**原理**

PCA 是一种经典的降维算法，它通过最大化数据方差来找到投影到低维空间后的主成分。

**步骤**

1. 对数据进行中心化，即减去均值。
2. 计算数据协方差矩阵。
3. 求解协方差矩阵的特征值和特征向量。
4. 选择前 k 个特征向量，将数据投影到对应的特征空间中。

**代码块**

import numpy as np
from sklearn.decomposition import PCA

def pca(X, n_components=2):
    """
    主成分分析算法

    参数：
        X: 原始数据，形状为 (n_samples, n_features)
        n_components: 降维后的维度

    返回：
        Y: 降维后的数据，形状为 (n_samples, n_components)
    """

    # 中心化数据
    X_centered = X - np.mean(X, axis=0)

    # 计算协方差矩阵
    cov = np.cov(X_centered)

    # 求解特征值和特征向量
    eigvals, eigvecs = np.linalg.eig(cov)

    # 降维
    Y = X_centered.dot(eigvecs[:, :n_components])

    return Y

**逻辑分析**

PCA 算法通过计算数据协方差矩阵的特征值和特征向量来降维。特征值越小，对应的特征向量越能表示数据在低维空间中的主成分。

#### 2.2.3 t分布邻域嵌入（t-SNE）

**原理**

t-SNE 是一种非线性降维算法，它通过最小化数据点之间的 t 分布相似度来构建低维流形。

**步骤**

1. 计算数据点之间的距离矩阵。
2. 将距离矩阵转换为 t 分布相似度矩阵。
3. 在低维空间中随机初始化数据点的位置。
4. 计算低维空间中数据点之间的 t 分布相似度矩阵。
5. 通过梯度下降最小化低维空间中的 t 分布相似度矩阵与原始 t 分布相似度矩阵之间的差异。

**代码块**

import numpy as np
import p