奇异值分解：特征向量的强大工具，拓展数据分析视野

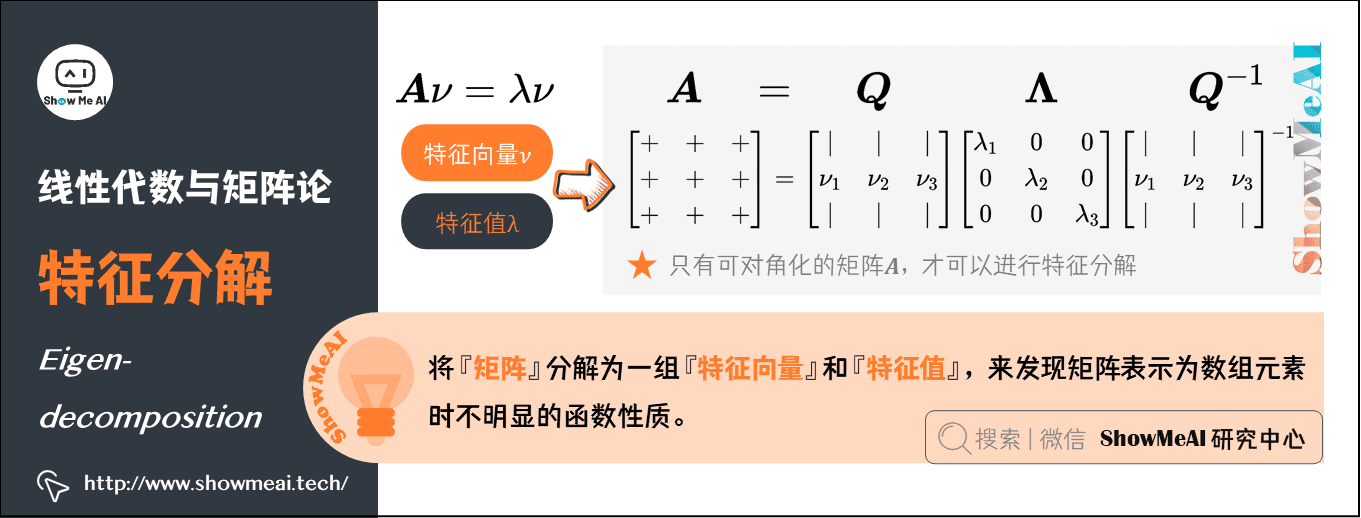
# 1. 奇异值分解的基本原理**

奇异值分解（SVD）是一种强大的数学工具，用于将矩阵分解为一系列奇异值和奇异向量的乘积。它在数据分析、机器学习和科学计算等领域具有广泛的应用。

SVD的基本原理是将一个m×n矩阵A分解为三个矩阵的乘积：

A = UΣV^T

其中：

* U是一个m×m的正交矩阵，包含A的左奇异向量。
* Σ是一个m×n的对角矩阵，包含A的奇异值。
* V^T是一个n×n的正交矩阵，包含A的右奇异向量。

奇异值是对矩阵A重要性的度量，较大的奇异值对应于矩阵中更重要的特征。奇异向量则表示这些特征在原始数据中的方向。

# 2. 奇异值分解的理论基础

### 2.1 奇异值分解的数学定义

奇异值分解（SVD）是一种线性代数技术，用于将一个矩阵分解为三个矩阵的乘积：

A = UΣV^T

其中：

* **A** 是一个 m×n 矩阵
* **U** 是一个 m×m 正交矩阵，其列向量是 A 的左奇异向量
* **Σ** 是一个 m×n 对角矩阵，其对角线元素是 A 的奇异值
* **V** 是一个 n×n 正交矩阵，其列向量是 A 的右奇异向量

### 2.1.1 奇异值

奇异值是矩阵 A 的特征值，表示矩阵沿其奇异向量的伸缩程度。奇异值按降序排列，最大的奇异值对应于矩阵中方差最大的方向。

### 2.1.2 奇异向量

奇异向量是矩阵 A 的特征向量，表示矩阵沿其奇异值的伸缩方向。左奇异向量是矩阵 A 的行空间的正交基，而右奇异向量是矩阵 A 的列空间的正交基。

### 2.2 奇异值分解的几何解释

奇异值分解可以几何解释为将矩阵 A 旋转到一个新的坐标系，使得 A 在新坐标系中的表示是一个对角矩阵。

**步骤：**

1. 首先，将矩阵 A 旋转到一个新的坐标系，使得 A 的左奇异向量成为新坐标系的基向量。
2. 然后，将矩阵 A 沿其奇异值缩放。
3. 最后，将矩阵 A 再次旋转到一个新的坐标系，使得 A 的右奇异向量成为新坐标系的基向量。

### 2.2.1 奇异值分解的应用

奇异值分解在数据分析中具有广泛的应用，包括：

* 数据降维和特征提取
* 图像处理和模式识别
* 自然语言处理和文本挖掘
* 机器学习和金融建模

# 3.1 数据降维和特征提取

**数据降维**

奇异值分解在数据降维中发挥着至关重要的作用。数据降维是指将高维数据投影到低维空间，同时保留数据的关键特征。这对于处理高维数据集非常有用，因为高维数据通常存在维度灾难问题，导致计算和存储成本急剧增加。

奇异值分解通过将数据矩阵分解为奇异值、左奇异向量和右奇异向量来实现数据降维。奇异值代表了数据方差的分布，而奇异向量则代表了数据在不同方向上的投影。通过截断奇异值和奇异向量，我们可以将数据投影到低维空间，同时保留数据中最重要的特征。

**特征提取**

奇异值分解还可以用于特征提取。特征是描述数据关键属性的变量。通过分析奇异向量，我们可以识别数据中最重要的特征。这对于模式识别、图像处理和自然语言处理等任务至关重要。

**代码示例**

import numpy as np
from sklearn.decomposition import TruncatedSVD

# 加载数据
data = np.loadtxt('data.csv', delimiter=',')

# 创建奇异值分解对象
svd = TruncatedSVD(n_components=2)

# 拟合数据
svd.fit(data)

# 获取奇异值和奇异向量
singular_values = svd.singular_values_
left_singular_vectors = svd.left_singular_vectors_
right_singular_vectors = svd.right_sin