特征向量分解：揭示数据内部结构，探索隐藏规律

# 1. 特征向量分解概述

特征向量分解（EVD）是一种数学技术，用于将矩阵分解为特征向量和特征值的集合。特征向量是矩阵中特殊的方向，特征值表示沿这些方向的伸缩量。EVD在数据分析、机器学习和信号处理等领域有着广泛的应用。

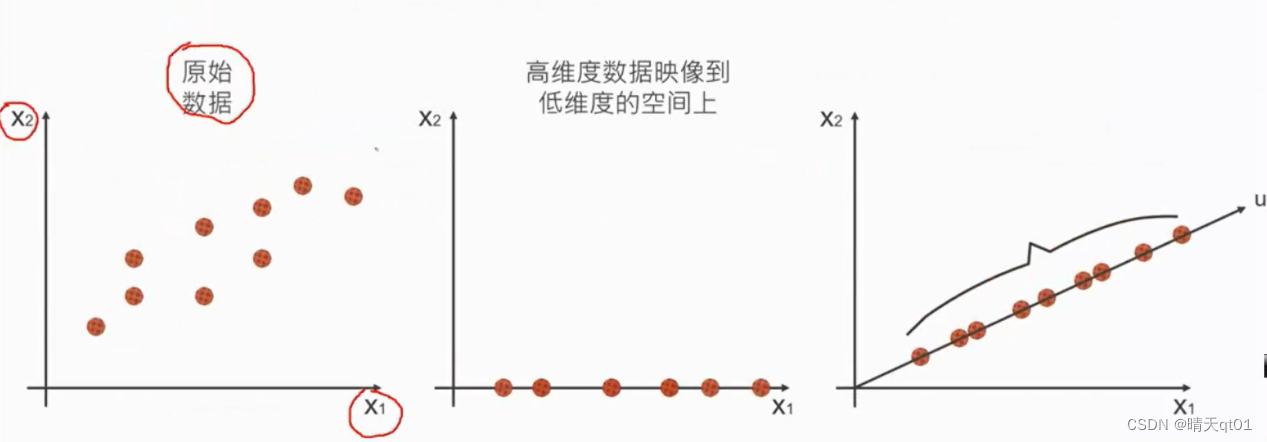
EVD的目的是将复杂的数据简化为更易于理解和处理的形式。通过识别数据中的主要特征，EVD可以帮助我们提取有价值的信息，揭示隐藏的模式，并提高算法的性能。

# 2. 特征向量分解理论基础

### 2.1 线性代数基础

**2.1.1 向量空间和内积**

向量空间是一个由向量组成的集合，满足以下运算律：

* **加法交换律和结合律：**对于任意向量 v、w 和 u，有 v + w = w + v 和 v + (w + u) = (v + w) + u
* **数乘结合律和分配律：**对于任意向量 v 和标量 c，有 c(v + w) = cv + cw 和 (c + d)v = cv + dv
* **单位元素：**存在一个零向量 0，使得对于任意向量 v，有 v + 0 = v
* **逆元素：**对于任意向量 v，存在一个向量 -v，使得 v + (-v) = 0

内积是向量空间中两个向量之间的运算，表示为 v · w，满足以下性质：

* **对称性：**对于任意向量 v 和 w，有 v · w = w · v
* **线性性：**对于任意向量 v、w 和标量 c，有 v · (cw) = c(v · w) 和 (v + w) · u = v · u + w · u
* **正定性：**对于任意非零向量 v，有 v · v > 0

### 2.1.2 矩阵的特征值和特征向量

矩阵 A 是一个由 m 行 n 列元素组成的数组。矩阵 A 的特征值 λ 是一个标量，使得存在一个非零向量 v，满足 Av = λv。向量 v 称为矩阵 A 的特征向量。

特征值和特征向量具有以下性质：

* **特征值是矩阵 A 的根：**矩阵 A 的特征值是其特征多项式 det(A - λI) = 0 的根。
* **特征向量是线性无关的：**矩阵 A 的不同特征值对应的特征向量是线性无关的。
* **特征向量张成矩阵的特征空间：**矩阵 A 的特征向量张成一个称为特征空间的子空间。

### 2.2 特征向量分解的数学原理

特征向量分解是将一个矩阵分解为特征值和特征向量的线性组合。常见的特征向量分解方法有奇异值分解（SVD）和主成分分析（PCA）。

**2.2.1 奇异值分解（SVD）**

SVD 将一个 m × n 矩阵 A 分解为三个矩阵的乘积：

A = UΣV^T

其中：

* U 是一个 m × m 正交矩阵，其列向量是 A 的左奇异向量。
* Σ 是一个 m × n 对角矩阵，其对角线元素是 A 的奇异值，按照从大到小的顺序排列。
* V 是一个 n × n 正交矩阵，其列向量是 A 的右奇异向量。

奇异值表示矩阵 A 的重要性，较大的奇异值对应于较重要的特征。奇异向量表示矩阵 A 在不同方向上的投影。

**2.2.2 主成分分析（PCA）**

PCA 将一个 n × p 数据矩阵 X 分解为一个 n × p 的正交矩阵 P 和一个 p × p 的对角矩阵 Λ：

X = PΛP^T

其中：

* P 是一个正交矩阵，其列向量是 X 的主成分。
* Λ 是一个对角矩阵，其对角线元素是 X 的主成分方差，